桥梁设计理论第八讲

《桥梁设计理论第八讲》由会员分享，可在线阅读，更多相关《桥梁设计理论第八讲（26页珍藏版）》请在装配图网上搜索。

1、第六讲 薄壁杆件的约束扭转第一节基本假定薄壁杆件的自由扭转是指杆件受扭时，截面的纵向翘曲位移不受约束，因而纵向翘曲应 变和相应的正应力都不存在。当截面的纵向翘曲位移受到约束时，便产生约束正应力和相应 的附加剪应力，这便是约束扭转。约束扭转的分析，可以从确定截面上纵向翘曲位移着手, 进而利用弹性理论的几何方程确定纵向翘曲应变；利用物理方程确定翘曲正应力；最后利用 微单元的平衡方程确定相应的翘曲剪应力。薄壁杆件的约束扭转分析中，除沿用前两章的若干基本假定（包括平面假定、线性假定、 小变形假定和周边投影不变形假定）外，补充的基本假定有：1、约束扭转产生的正应力和剪应力沿壁厚均匀分布（参见图5-7），

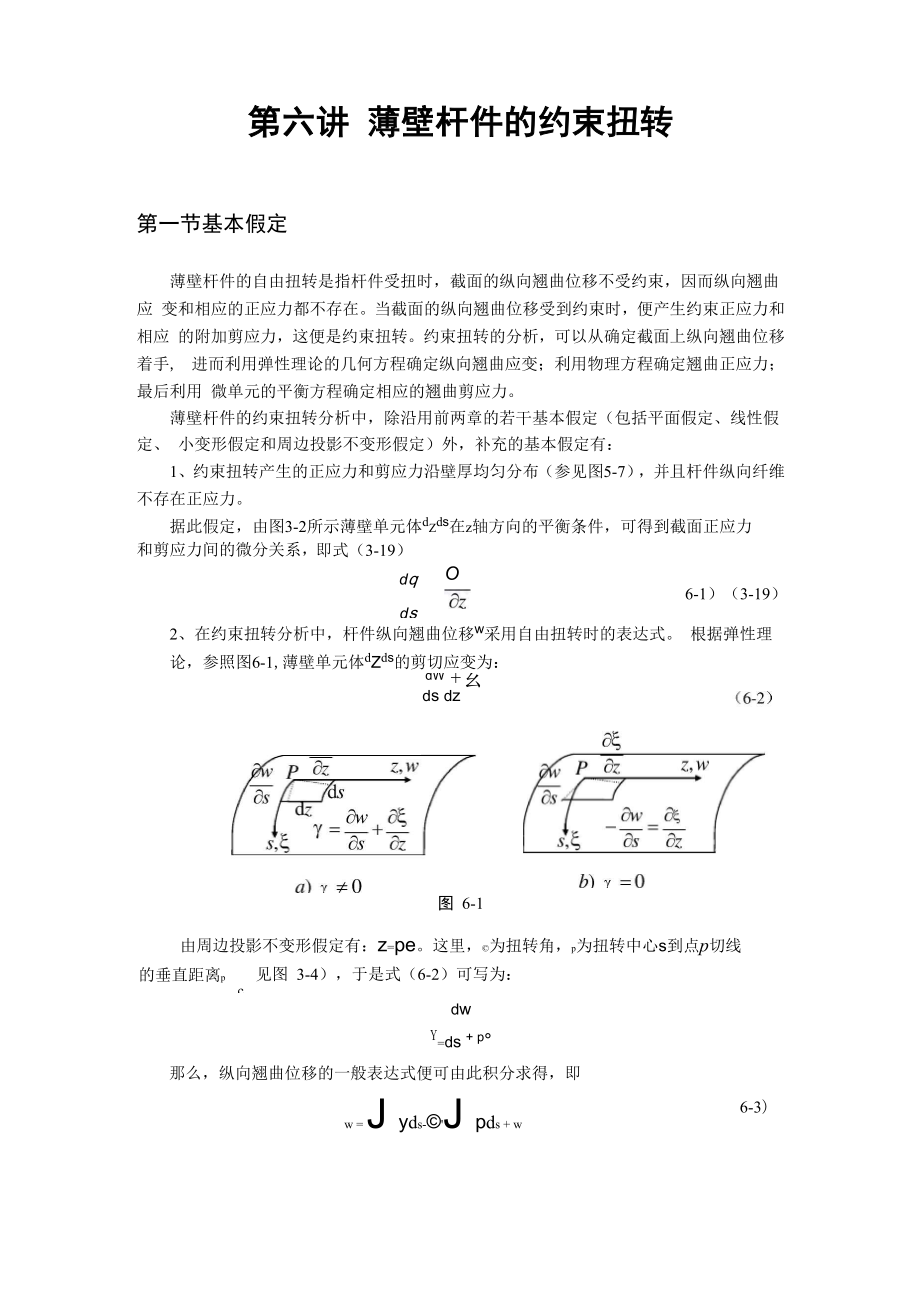
2、并且杆件纵向纤维 不存在正应力。据此假定，由图3-2所示薄壁单元体dZds在z轴方向的平衡条件，可得到截面正应力和剪应力间的微分关系，即式（3-19）dqdsOg6-1）（3-19）2、在约束扭转分析中，杆件纵向翘曲位移w采用自由扭转时的表达式。 根据弹性理论，参照图6-1,薄壁单元体dZds的剪切应变为：dW +玄ds dz图 6-1由周边投影不变形假定有：z=pe。这里，为扭转角，p为扭转中心s到点p切线的垂直距离pc见图 3-4），于是式（6-2）可写为：dwY=ds + p那么，纵向翘曲位移的一般表达式便可由此积分求得，即6-3)w = J yds-J pds + wss0式中w0为s

3、 =0处的翘曲位移值。参照第三讲剪力中心推导中关于扇性坐标的定义有6-4)(3-30-1)二j pdss式中b为自积分起点至扇性零点（s =0，b二）到s点所包围的扇性面积的2倍。于是，纵向翘曲位移的一般表达式（6-3）可写为：6-5)w 二 Jsy dsQb+w00对于开口薄壁杆件，其在中面上的自由扭转剪应变y十=0，代入上式便得截面的纵向翘中曲位移表达式6-6)对于闭口薄壁杆件，其在中面上的自由扭转剪应变丫中丰0，根据虎克定律Y=，分 别按单室或多室闭口截面确定剪应力1剪应变y。对于单室截面，剪应力工由式（5-38）给出，于是，剪应变y可写成:6-7)_t My_G 二 2GAt式中自由扭

4、转矩二 GI Q，= G4A2Q，Tds6-8)将式（6-7），式（6-8）代入式6-3)，化简后便可得：w 二-Q js (p 2A )ds + w 0护 0t6-9-1)其中：w = -b + w06-9-2)b 二（p 2A ）ds =b js 2A ds0 匹。匹tt称为广义扇性坐标，它表示产生单位扭转角（Q=1）时的纵向翘曲位移，2 AM6-10)因此，常称为单位翘曲。显然，其中第二项j击则为计及中面自由扭转变形y =2GAt影响的修正项, tt此即与开口截面（=）的差别所在。中对于多室截面，在剪切变形表达式中，引入相应的剪力流，即将以下各式q tiq. =q. -2-i i I和M

5、GITT代入y=G中得到多室截面自由扭转变形剪应变:1 q _ 2qMtGi，29咛T对于截面周界壁和交界壁则分别为：q 截面周界壁上：y=乃鱼- t(q q ) t丿将式(6-11)代入式(6-3)后积分，w _-9 j截面交界壁上：丫=乃得到多室截面翘曲位移表达式如下:周界壁：交界壁：w _ - Js0_ q Yp 2 车 ds + w o k t丿(q q ) k t丿ds + w06-11-1)(6-11-2)或统一写成：式中：周边交界p 2-L. ds _ w 2f s kt 丿(q q )t丿p2里dss tds _ Ei_q dss t(6-12)6-13-2)6-13-2)上式

6、展开并引入扇性坐标后，改写为：q 周界壁w_w 2f i ds(6-14)0t交界壁w _w 2Js纟J_qkds0 tw称为闭口截面的广义扇性坐标，当以扭转中心为极点，以主扇性零点(M0)为积分 起点(s =0)时，则称为主广义扇性坐标。上述推导中均引用了自由扭转的剪切特性。为计及约束扭转引起的翘曲剪应力的影响，苏联学者YMANCKM财建议以一待定函数 (z)来代替扭转角9 (z)，即将式(6-12)写成：w_-6(z)w(s) + w (z)(6-15)0这便是闭口截面约束扭转翘曲位移的表达式，它具有与开口截面翘曲位移式(6-6)相 似的形式。由于式(6-5)为纵向翘曲位移的一般表达式，其

7、中剪应变y沿用了自由扭转的有关公式，对于开口截面，式（6-6）中显然忽略了沿壁厚均匀分布的约束扭转剪应力产生的剪应 变；对于闭口截面，式（6-15）也只是近似地计及了约束扭转剪应力的影响。故本书将纵向 翘曲位移表达式（6-6）,式（6-15）视为约束扭转分析的一种基本假定。第二节 开口薄壁杆件的约束扭转本节将按上节指明的约束扭转分析步骤讨论开口薄壁杆件的约束扭转问题。如上节所述，开口薄壁截面的纵向翘曲位移W = g W）一、纵向翘曲位移这里，w = JsPds为以扭转中心为极点，任选曲线坐标起算点的扇性坐标，其中）w0二w0（z）为待定的积分函数，它表示起算点处的纵向翘曲位移。二、约束扭转的正

8、应力引用弹性理论的几何方程，可直接写出纵向翘曲应变为：zdw丄， = W + Wz dz0根据物理方程虎克定律及杆件纵向纤维间不存在正应力的基本假定，可得出约束扭转正应力为：wb = E E（w + W ）w z0式中待定函数w0可由静力学方程来确定，注意到截面内力中除M_丰0外，其余内力N 0， M 0， M 0xy6-16)z因此，约束扭转正应力在截面上是自相平衡的Jso b tds 二 00w即其合力为零。6-17)注意到A二J%tds，将式（6-16）代入式（6-17）后得到待定积分函数）sowtds6-18)W =00A将式（6-18）代回式（6-16）有：-E w - 一 Js0

9、wtds 6-19)I A 0丿w w Js0 wtds0 A 0适当地选择曲线坐标起算点（s =0），使积分Js0 w tds 00式（6-19）中，w0 w。相应的起算点称为主扇性零点，当满足条件式（6-19）有几个点时，则以距扭转中心最近的扇性零点为主扇性零点。基于主扇性零点的坐标称为主扇性 坐标，利用这一特点，当主扇性零点易于判断确定时，将简化主扇性坐标地计算，详见第五 节算例。对于主扇性坐标，由式（6-18）得到：w0 =常数其物理意义为：主扇性零点处的纵向翘曲位移为沿杆轴向为常数。即主扇性零点处无翘 曲应变，翘曲正应力为零。于是，用主扇性坐标表达翘曲位移时，时（6-19）可简化为o

10、 二 _EO0即翘曲正应力按主扇性坐标（3 0）的规律分布。三、约束扭转剪应力利用式（6-1）表示扭转正应力与剪力流的关系式理+1旦二0dsdz6-20)(6-21)将式（6-20）表示的约束正应力代入上式移项后积分，可得开口薄壁截面约束扭转剪力其中：q 二 J sEoQtds + qO 0 0 0q 二 ES+ qO O 0S = Js o tdsO 0 06-22)6-23)流：称为扇性静矩。显然，式（6-22）中积分常数q0为积分零点处的剪力流。对于开口薄壁截面，当积分 零点选在开口处的自由边缘时q0二0，贝哟束扭转剪力流的最后表达式（6-22）可简化为: q = ESo（6-24）OO

11、而约束扭转剪应力为：ES I T = d（6-25）Ot观察上述各式可知，开口薄壁杆件约束扭转正应力和剪应力的计算涉及到扭转变形1 和e,因此，需先求出杆件的约束扭转变形（在下一讲讨论）e，再根据截面的扭转中心 和主扇性零点，计算主扇性坐标和扇性近矩，最后利用式（6-20）及式（6-25）求算开口薄 壁截面约束扭转的正应力和剪应力。四、约束扭转双力矩和约束扭转力矩在前二章关于弯曲和自由扭转分析中，弯曲正应力，弯曲剪应力，自由扭转剪应力等都 采用截面内力以及截面几何特性来表示，而本章约束扭转正应力和剪应力贝没有以相应的截 面内力表示。为取得更为直观的物理概念，将约束扭转正应力和剪应力与截面内力和

12、几何特 性相联系，因此式（6-20）和式（6-25）表示的约束扭转正应力和剪应力合成为截面内力。则：B = Jso w tds 二EJs w2tds0 -EI 0 w 0 w 0 0 0 w Js t p tds Js q p ds eJs J0 w 00 w 00 L(E w Jsw tds -Jsw2tdsIoL 0 0 00 0 w0w0s tds p dsd o 0.00= EI 慣w6-26)6-27)注：式中由于w0为主扇性坐标，因此，hw0tds = 。其中：6-28)I = Js w 2 tdsw 0 0/w称为截面的主扇性惯矩。M为约束扭转剪应力合成的力矩。故称为约束扭转力矩

13、。 wwB则称为约束扭转双力矩，它是正应力以扇性坐标为“力臂”合成的广义力矩。在如图6-2a CO所示的工字型截面中，B表现为大小相等方向相反，分别作用在两翼缘板内的一对力偶， co故形象的称之为双力矩。从图6-2b）也可看到对应于这样的双力矩，截面变形呈“翘曲”状态，故这种约束扭转正应力和剪应力又称为翘曲正应力和翘曲剪应力。显然，由式（6-26）、（6-27） 系：可见，约束扭转双力矩和约束扭转力矩之间有下列微分关ydB= ww y dzy (6-29)将式6-25），yB（6-26）表示的 0二一廿及式（6-27）表示的0 - wEIEIww可得到用截面内力和几何特性表示的约束扭转正应力及

14、剪应力计算公式如下BwO = w_0-wIwMS11w代回式（6-20）及式6-30)五、约束扭转与梁平面弯曲的比较分析式（6-26）、（6-27）、（6-29）及式（6-30）可见，约束扭转的基本方程与梁的平面弯曲基本方程具有相似的数学表达式。为便于记忆。现将二者综合比较列于表6-1。梁的平面弯曲与开口截面约束扭转比较 表 6-1内容平面弯曲（y 一 z平面）约束扭转挠度w扭转角e位移转角e单位扭转角e静矩S ytds扇性静矩S =Js- tds截面几X fs 0 0何特性惯矩 1 =Jsy 2tdsxC扇性惯矩1 =Js_ 2tds0 0 0弯矩 M =E1 w扭转双力矩B = -E1 e

15、xxcoco剪力 Q = E1 w扭转力矩M =-E1 e内力yyCOco分布荷载分布扭矩q = Q = M = El wm =-M =-B = E1 eyyxxCOcococoM yB 正应力正应力 =_-z1 1应力xQScoM S剪应力e =-yz1 t剪应力e-_-_1 tCO微分方程E1 w = qE1 e = mxyCOco第三节闭口薄壁杆件的约束扭转一、纵向翘曲位移闭口截面约束扭转的纵向翘曲位移采用式（6-15）,它具有与开口截面相似的形式，以 代替，以待定函数代替扭转角e，即有：w = -6+ w0（6-31）（6-15）二、单室闭口截面的约束扭转正应力由于闭口截面的纵向翘曲位

16、移具有与开口截面完全相似的形式，故其约束扭转正应力可 对比开口截面直接写出，不再推导。6-32）（6-20）6-33）（6-19）6-34）（6-26）6-35）（6-30）6-36）（6-28）= -EO0而o- 丄 kotds而0A如果用约束扭转双力矩B-表示，则有：OB_ = -El_ 9 ” B_O 二-_O l/_ = 2tds-0其中1_可用-与s图图乘计算得出。-三、单室闭口截面的约束扭转剪应力约束扭转剪应力同样可对比开口截面的扭转剪应力公式（6-22）及式（6-23）直接写出。6-37）q_ =t_ t = ES_ V + q33w0其中：3二 j s0w tds006-38）

17、闭口截面没有自由边缘，q0值不能直接定出，参照第三讲第五节闭口截面弯曲剪应力的做法，将闭口截面“切开”使其成为开口截面，在切口处加上赘余力，若曲线坐标积分起点取在切口处，则式（6-37）中q即为切口处的赘余力，而ES即为相应的开口截面剪03力流。q0仍根据切口处的变形连续条件求解，即ds 二 06-39）将式（ 6-37）代入，移项得：EoJS 兰6-40）3 tq0 = jds_将式（6-40）代回式（6-37）得:其中：q 二 ES33S = s_1 sg/l333 tdst称为广义扇性近矩。于是，得到闭口截面的约束扭转剪力流q_ 二 ES33和开口截面类似，引入约束扭转力矩M3，则有：3

18、M_ 二-EI_933I- 13 2 tds30M SX 333I_t3四、多室闭口截面的约束扭转剪应力（ 6-41）（ 6-42）（ 6-43）6-44）（6-27）6-45）（6-28）6-46）（6-30）对于多室截面，仿照第三讲第五节将各室“切开”，确定各室赘余剪力流q0.，与各室安 0i开口截面解得的约束扭转剪力流q叠加，即参照式（2-41）不难求出多室闭口截面约束扭 3i转的总剪力流。即q- q - + q（周边）（6-47-1）3i3i0iq_. q- + q. q （交界）（6-47-2）3i3i0i0k其中q仍由各室切口处的变形连续条件给出的线形方程组求解。即0iI Y _

19、ds 二 0i 由式（6-47）,并根据虎克定律及剪力流的定式（2-3）,便有:YCO=善二 G (q -+q._ q0k)代入前式，并注意到在截面上q =常数（与s的坐标无关），得到线性方程0i6-48)dsdsdsq+ q- q= 0i t0i t0k i,k t式中开口截面约束扭转剪力流q-可仿照（6-30，写成iM_ Qq_ S -iI co(6-49)代入式（6-48）并移项后得到：dsdsMdsq qS 0i i t0ki,kt I i - tCO6-50)M用式(6-50)除以了亠，并令：COMM_q q ； q q0i 0i /_，0k0k /_coco6-51)于是，式( 6

20、-50)转化为：入 I ds 入 I ds Idsq - q S(i 1,2, n)0i t0k ik t- dt6-52)(3-41)对于n室闭口截面，此式提供了求解 q，的线形方程组，而未知数q则表示当0k0iMi- 1时，各室的约束扭赘余剪力流。显然，当基本体系（开口截面）对于主扇性坐标的静矩S为已知时，即可根据（6-52）求解。CO将式（ 6-51）及式（ 6-49）代入（ 6-47）便有刃M _q_ _ S_i I_co其中：S- s_ q0 （周边）0i( 6-53)6-54-1)-q0k)交界）6-54-2)称为多室截面的广义扇性静矩，它表示截面约束扭转翘曲剪力流的分布规律，故又

21、称为约束扭转翘曲剪力流的分布函数。至于多室截面的主扇性惯矩1-，则由单室截面的定义式（6-45）不难写出1 -工1 _2tds（6-55）i 0可应用_0图进行图乘计算/_,式中i表示截面的壁段。0第四节 薄壁截面的扇性特性上两节分析表明，无论开口或闭口截面，约束扭转的分析都归结为与弯曲分析相类似的 的形式，但具体求解则繁复的多。首先是相应于挠度的扭转角系约束扭转和自由扭转的综合 效应，因而还不能按表6-1 给出的扭转角微分方程单独求解。此外。截面扇性几何特性的计 算也远较弯曲分析中几何特性的计算复杂得多，为此，将开口和单室闭口截面的扇性几何特 性的一般公式归纳于表6-2。项目开口截面单室闭口

22、截面多室闭口截面扇性 坐标=Js pds02 A ls ds 二_ r Js J色0 t-2 (q -q )竺0 ik t主扇 性 坐标 =-丄 Js0tds0 A 0(1) 以扭转中心S为极点(2) Js0 tds 二 00 0=-丄 J tds 0 A(1) 以扭转中心S为极点(2) J tds = 0-丄工 Jtds0Ai条件同左.扇性 静矩S = Js tds 0 0 零点取在开口边缘/J S上S s ts s f i- -ldsS_ - Js tds- 0 0扇性零点取在切口处s_ s_ - (q - q) 0i0ks_ Js tds- 0 0扇性零点取在切口处扇性 惯矩I 二 Js

23、0 2 tds 0 0I- J 2 tds 0I-乙 J 2 tdsi0第五节 算 例例6-1如图2-6a）、b）所示单箱双室截面和工字型截面，试分别计算其主扇性坐标叫, 0，主扇性静矩S-，S，主扇性惯矩1-,1。截面尺寸如图所示。0【解】首先将开口截面和闭口截面约束的计算公式对比如下，以便确定计算步骤。项目开口截面闭口截面双力矩B -EI 慣 copco其中：I Js0 2 tds 八.00B_ -EI_ VCOfw其中：I_ J 2tds八0约束扭转力矩M -EI 畀COcoM_ -EI_9 ”(D(D约束扭转正应力B wB_b_ _&0IICO其中:Js pds0 0其中：d sJsp

24、-2(q -q )一00ik tTM SM_S_I tpcoS JstdsT约束扭转剪应力COI_tco其中：其中：S- S -(q q ) 0 00i0k由上述各式可知，薄壁杆件约束扭转计算的步骤是：1、计算截面形心及形心主轴；2、以形心为极点，任选扇性零点C ；3、计算截面对形心主轴的惯矩1 M M M ；x y4、计算截面扭转中心的坐标（, y0）及主扇性零点M0；5、计算截面主扇性坐标0或% ；6、求主扇性惯矩厶、及极惯矩1 n （下一讲讨论）；P7、求扭转微分方程，求扭转变形0 ；8、求B及M （或B_及M_）；COCOCOCO9、 计算翘曲应力Q及T（或b及T 一）；co coCO

25、 co一、确定截面坐标由扭转中心的计算公式（3-28）、（3-31）、（3-45）及式（3-51）不难得知，无论开口和 闭口截面，截面的对称中心即为剪力中心（扭转中心）。又由式（6-19）可以推知，对称轴与截面中线的交点均为扇性零点，而扭转中心最近的 扇性零点为主扇性零点。应用这些结论可以省去许多繁冗的计算。本例因中腹板通过对称中心，故扇性零点均与对称中心重合。二、工字型截面1、主扇性坐标由式（ 6-4）及式（ 6-19）co0=(二 Js pds0式中0系扭转中心S为极点，主扇性零点（M0 ）为积分起点（s =0），曲线坐标以绕扭转中心逆时针为正，对于工字型截面（见图6-3），据上述分析，应

26、以Sf为起始矢径进行计算，故由图（6-3a）有:a |t 二 0.1=0.3S |(M )-01.5c_g -1.51.5-1.5S -(M )01.01.0a）构造图-1.5cdd-1.5a) 图0图 6-3a) Sw 图w0,M00, f）=1.5X1.0=1.5 （m2）0,a/ Tk段：w =1.5X（-1.0） =-1.50,k利用截面的对称性（w0呈反对称），做w0图如图（6-3b）所示。2、主扇性静矩以开口截面自由边（图6-3中的k或c）为积分起点（满足q0=0）， 转中心逆时针转为正。(m2)曲线坐标s以绕扭S = f sw tds w 0 0 由图（6-3b）可知，w0为s的

27、线形函数，即w =-1.5 （1.0 s ）0a)务必指出，在求w图时采用的积分起点（s =0）和这里求S可以不一致，但当将式（a） 0w代入（6-23）具体计算时，就应将已有的w0与S取相同的积分起点建立方程，如上式所示。0 w已知翼缘壁厚t =0.1m，于是将（a）代入（6-23）得：S 二 f sw tds = -0.15f s（1.0 - s）ds0 0 0S =-0.15（1.0s -1 s 2）2b)k 点：S=0 (s = 0),kf 点：S=-0.075 (s = 0),fa占.八、S,a=0 (s = 0)则各特征点的 S 为：c)利用对称性，作出S图如图（6-3c）所示。C

28、O主扇性惯矩对w0图（见图6-3b，应用图乘法得到:I = J 幼 2tds = 4 X 0.11 X 1.0 X1.52 （1.5） = 0.30（m4） 0 o23三、单箱双室截面单箱双室截面的扭转中心、主扇性零点均位于对称中心。1、主广义扇性坐标由式（6-14）知广义扇性坐标为：d）e）e = e - 2J s（q q ）-0 i kt其中相应的开口截面扇性坐标如式（6-4）e = j s pds0由于上二式计算均取主扇性零点为积分起点，故式（d）、式（e）即为相应的主扇性坐 标0及0。f）现已知道t =0.1m,由第三章例3-1已求得q. 0.06，故对于截面周边由式（6-13）有:

29、-2 sq ds = - 2 f sq ds = 2 x 0.06s0 i t t 0 i 0.1 -2J sq ds = -1.2s0 i t对于交界腹板fd，因其通过扭转中心，且q二q，故ikg） = 2丿（q q ）ds = 0fi,k i k t于是，根据式（e）,取/点为切点，并以该点为各点曲线坐标的起算点（见图6-4b）, 计算如下： = 0f左 = 0 +1.50 x1.00 = 1.5（m2）a = 1.50 +1.00 x 3.00 = 4.5（m2）c = 4.5 +1.5 x1.00 = 6.00（m2）d（注意到f T d之为零）（、 二 6.00+1.50x1.00

30、二 7.52 丿 = 7.50+3.00 X1.00 = 10.50（n2）二 10.50+1.50x1.00 二 12.00（B2）f右ds按式（f）计算-2f sq =1.2s，如图（6-4c）所示。0 i tf 左点一1.2s =0 （ s = 0 ）a占八、c占八、 1.2s = 1.20 (m2) 一1.2 s =一4.80( m2)g 点1.2 s =7.20(m2 )k占八、/右点1.2s=10.80(m2)1.2s=12.00(m2)将图（6-4b）叠加，即得到主广义扇性坐标莎图，容易看出，沿周边s呈线形分布, 其各特征点的坐标（如图6-4d）所示为：E =m =m = 0f

31、b h/E =-E 二E =-E 二 0.302/a c g k2、广义扇性惯矩根据式（6-3b ）及E图，不难计算广义扇性惯矩h)/_ 二 Js e 2dsE o于是根据E图（图6-5d）应用图乘法有:1 2 1 2I= 4 x 0.12 x 1.50x 0.30x 3 0.30) + 2 x 1.00x 0.30x 3 (0.30)二 4(0.030+ 0.045)二 0.075x 4 二 0.30(m4)3、相应的开口截面静矩将截面在某一位置（图6-4e）切开，使其成为开口（静定）截面，其相应的静矩S_ = J sE tds（k）E 00现t =0。10m,由于E图为s的线形函数，故知S

32、_为的s二次函数。取切口处为积分起E点s =0,计算S-的特征点值如下：E/点a占八、b占八、c占八、d占八、S_ = 0-fS_ =1 x1.00 x 0.30 x 0.10 = 0.0 1$n4）-,a 2S = 0.015+1 x1.50 x 0.30 x 0.10 = 0.0375（m4）E ,b2S_ = 0.0375+1 x 1.50（-0.30） x 0.10 = 0.015（m4）-,c2S_ = 0.015+1 x 1.00（-0.30） x 0.10 = 0,d2由-图不难推知，S_应呈正对称，应用二者的微分关系，便可确定S_图的凹凸性， 得出S-图如图（6-4e）所示E4

33、、广义扇性静矩 根据式（6-54）广义扇性静矩S- - S- - （q - q ）E E0i0k其中q需求解线性方程组（6-52）确定，即idsq0i ti0.020.02ka -1.2 fc) -2如半图I丨丨丨丨丨10.02S-h_0.02f) q0图0ig)S o 图图 6-4现t =0.10m, i =1,式中系数J ds = 1 ds 二 2 x (3.0 +1.0)二 8.0(m)122,则上式可写为：q J ds - q Jds = J S ds01 102 1,21 广-q Jds - q Jds = J S ds01 2,1 02 2 2 o二部图层-5）二部荷载坐用系 错横

34、未矩 蠶向笹应力 脳，zxp（s,z）T约束扭转双力矩=J s0a tds030J ds = J ds 二 3.0（m）1,2 2,1常数项由S_ （见图6-4e）对s积分得到，即COJ S_ds = J S_ds = 2X1X 0.015x1.0 + 0.015x 3.0 + - x 3.0（0.0375 0.015） = 0.10（m6） 1 32 333将系数及常数代入式（1）,8q 3q 二 0.1001023q + 8q 二 0.100102解方程组的：q01= q02二0.20 据此作出.图如图（6-4f）所示。i根据式（6-54）将q0图与S_图叠加，得到如图（6-4g）所示的主

35、惯性静矩S-图。0i33第六节 小 结1、薄壁杆件受扭时，截面的纵向翘屈位移受到约束，则称为约束扭转。约束扭转正应力合成约束扭转双力偶，而对应于约束扭转正应力的约束扭转剪应力，则合成约束扭转力矩， 对于开口截面约束扭转力矩Ms0T p tds3 0 3 02、约束扭转分析中，采用自由扭转分析得出的翘曲位移表达式，对于闭口截面，由于 自由扭转剪应力沿壁厚均匀分布，中面剪应变不为零，扇性坐标采用修正公式（6-10）、式（6-14）,当计及约束扭转的剪应变的影响时，翘曲位移采用式（6-15）,其中为待定函数。便有：B 3B_ 3开口O二3_0闭口 O=十_3|COcoMSM S开口T=33闭口 T

36、二一约束扭转正应力：约束扭转剪应力：3、根据翘曲位移模式，引用几何方程求得正应变，又根据虎克定律求得相应的约束扭 转正应力，由薄壁微分单元的静力学平衡条件求出相应的附加剪应力。当以约束扭转双力矩 和约束扭转力矩表示时4、约束扭转力矩和双力矩与约束扭转变形（或 ）间的基本微分方程为：开口 EIQ = -B闭口 EI = -BCOcococo开口 EI e = M闭口 EI_ = M_COcococo比较上述各式与梁平面弯曲的基本方程有表6-1的对应关系。5、约束扭转分析中采用了截面扇性几何特性，有关计算公式见表6-26、无论开口或闭口截面，其剪切中心位于截面的对称轴上，扇性零点在对称轴与截面 中线的交点上。