261双曲线地性质

《261双曲线地性质》由会员分享，可在线阅读，更多相关《261双曲线地性质（8页珍藏版）》请在装配图网上搜索。

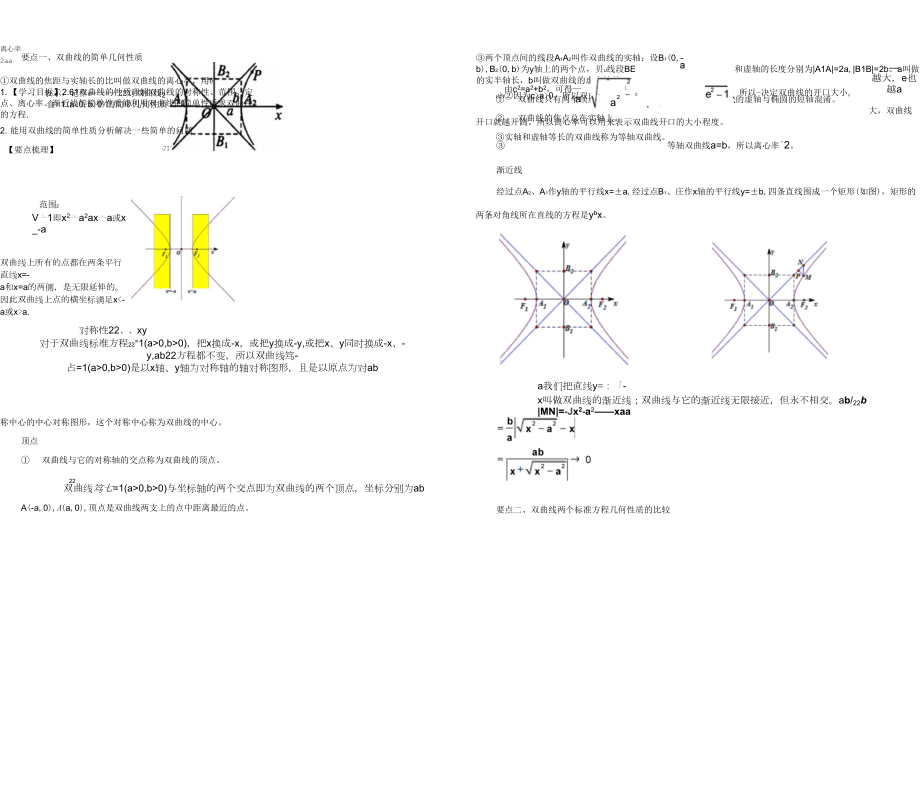
1、1. 【学习目标】2.61双曲线的性质理解双曲线的对称性、范围、定点、离心率、渐近线等简单性质能利用双曲线的简单性质求双曲线的方程.2. 能用双曲线的简单性质分析解决一些简单的问题【要点梳理】两个顶点间的线段A1A2叫作双曲线的实轴；设B1(0,-b),B2(0,b)为y轴上的两个点，贝U线段BE2叫做双曲线的虚轴。实轴和虚轴的长度分别为|A1A|=2a,|B1B|=2b。a叫做双曲线的实半轴长，b叫做双曲线的虚半轴长。 双曲线只有两个顶点，而椭圆有四个顶点，不能把双曲线的虚轴与椭圆的短轴混淆。 双曲线的焦点总在实轴上。 实轴和虚轴等长的双曲线称为等轴双曲线。离心率要点一、双曲线的简单几何性质

2、双曲线的焦距与实轴长的比叫做双曲线的离心率，用e表示，记作e=22Xy双曲线2-食=1(a0,b0)的简单几何性质ab因为ca0，所以双曲线的离心率e=1。2aa所以-决定双曲线的开口大小,2a由c2=a2+b2，可得=aJI范围2V亠1即x2亠a2ax亠a或x_-a双曲线上所有的点都在两条平行直线x=-a和x=a的两侧，是无限延伸的。因此双曲线上点的横坐标满足xa.对称性22、xy对于双曲线标准方程22=1(a0,b0)，把x换成-x，或把y换成-y,或把x、y同时换成-x、-y,ab22方程都不变，所以双曲线笃-占=1(a0,b0)是以x轴、y轴为对称轴的轴对称图形，且是以原点为对ab越大

3、，e也越a大，双曲线开口就越开阔。所以离心率可以用来表示双曲线开口的大小程度。 等轴双曲线a=b，所以离心率2。渐近线经过点A2、A1作y轴的平行线x=a,经过点B1、庄作x轴的平行线y=b,四条直线围成一个矩形(如图)，矩形的两条对角线所在直线的方程是ybx。a我们把直线y=：-x叫做双曲线的渐近线；双曲线与它的渐近线无限接近，但永不相交。ab/22b|MN|=-Jx2-a2xaa要点二、双曲线两个标准方程几何性质的比较称中心的中心对称图形，这个对称中心称为双曲线的中心。顶点 双曲线与它的对称轴的交点称为双曲线的顶点。22双曲线笃七=1(a0,b0)与坐标轴的两个交点即为双曲线的两个顶点，坐

4、标分别为abA(-a,0),A(a,0),顶点是双曲线两支上的点中距离最近的点。标准方程22xyr=1(aA0,bn0)ab22yxp-p=1(a0,b0)ab图形1/blA210It1110X輕性质焦占八、八、c,0),F2(c,0)F1-c),F2(0,c)焦距IF1F2I=2c(c=Ja2+b2)IF1F2I=2c(c=Ja2+b2)范围xx兰-a或xza，yeRyy兰一a或y3a,R对称性关于x轴、y轴和原点对称顶点(a,0)(0,土a)轴实轴长=2a，虚轴长=2b离心率e=c(e1)a渐近线方程.by=士xa.ay=xb(3)与双曲线22X2一y2=1有公共渐近线的双曲线ab22与双

5、曲线X驚=1有公共渐近线的双曲线方程可设为a2b20，焦点在y轴上)(4)等轴双曲线的渐近线22Xy2-y2=G-0)G*0，焦点在x轴上,ab等轴双曲线的两条渐近线互相垂直，为y=_x，因此等轴双曲线可设为x2_y2=(=0).要点四、双曲线中a,b,c的几何意义及有关线段的几何特征:双曲线标准方程中，a、b、c三个量的大小与坐标系无关，是由双曲线本身的形状大小所确定的，分别表示双曲线的实半轴长、虚半轴长和半焦距长，均为正数，且三个量的大小关系为：cb0,ca0,且c2=b2+a2。22Xy双曲线=1(a0,b0)，如图：ab叫J(1)实轴长|AA21=2a，虚轴长2b,焦距|F1F2卜2c

6、,(2)离心率:”ipF1LipF2LlAF1lPM1I1PM2I1AK1IIA2F2IIA2K2I(3)顶点到焦点的距离:IafJTAzF=ca,IAF2|=|人冃=a+c；要点诠释：双曲线的焦点总在实轴上，因此已知标准方程，判断焦点位置的方法是：看X2、y2的系数，如22果X项的系数是正的，那么焦点在X轴上；如果y项的系数是正的，那么焦点在y轴上。对于双曲线，a不一定大于b，因此不能像椭圆那样通过比较分母的大小来判定焦点在哪一条坐标轴上。要点三、双曲线的渐近线(1)已知双曲线方程求渐近线方程：(4)也PF1F2中结合定义|PF1-PF=2a与余弦定理，将有关线段PR、PF2、F1F2和角结

7、合起来22若双曲线方程为务-乂y=1，则其渐近线方程为aba2(5)与焦点三角形厶PF1F2有关的计算问题时，常考虑到用双曲线的定义及余弦定理(或勾股定理)、1角形面积公式Spf1f-|PF1PF2sinZF1PF相结合的方法进行计算与解题，将有关线段|PR、|PF2F1F2,有关角NF1PF2结合起来，建立PF1-PF2、PF1PF2之间的关系.已知双曲线方程，将双曲线方程中的“常数”换成“0”，然后因式分解即得渐近线方程。(2)已知渐近线方程求双曲线方程：若双曲线渐近线方程为mx二ny=0，则可设双曲线方程为m2x2-n2y2=，根据已知条件，求出即可。【典型例题】类型一：双曲线的简单几何

8、性质例1.求双曲线16x29y2=144的实轴长和虚轴长、顶点坐标、焦点坐标、渐近线方程与离心率2【解析】把方程化为标准方程y92x1,16由此可知实半轴长a=3,虚半轴长b=4,.c=.a亠b5双曲线的实轴长2a=6，虚轴长2b=8，顶点坐标(0,-3),(0,3)，焦点坐标(0,-5),(0,5),离心率e=c=5，渐近线方程为y=3xa34【总结升华】在几何性质的讨论中要注意a和2a,b和2b的区别，另外也要注意焦点所在轴的不同，几何量也有不同的表示22焦点在y轴上)，则其渐近线方程为二一厶=0二.x_y=。二.gnx.mnmnm举一反三：【变式1】求下列双曲线方程的渐近线方程22(1)

9、-y1;(2)x2-2y2=8;(3)y2-2x2=721636【答案】(1)y-x;(2)y2x;(3)y-,2x22举一反三：【变式1】双曲线mx+y2=1的虚轴长是实轴长的2倍，则m等于()B.C.44【答案】A1d.-42x2【变式2】(2015北京)已知双曲线-y-1(a0)的一条渐近线为3y=0,a【答案】【变式2】已知双曲线228kxky=2的一个焦点为3(0二)，则k的值等于(A.2B.1C【解析】渐进线为y=0，.有-=-.3，由双曲线的方程aa2y2=1得b=1,且a0所以【答案】C类型二：双曲线的渐近线例2.已知双曲线方程，求渐近线方程。(1)x22y=116；(2)-1

10、916【解析】(1)双曲线2y_916-1的渐近线方程为:201622(2)双曲线x916二-1的渐近线方程为:916一0【变式3】(2016北京文)已知双曲线x2(a0，b0)的一条渐近线为2x+y=0，一个焦点为(J5,0)，贝Ha=;b=.c-、5【答案】依题意有b，结合c2=a2+b2，解得a=1，b=2。2a例3.根据下列条件，求双曲线方程。22_与双曲线x-y-1有共同的渐近线，且过点(-3,2、一3);916一渐近线方程为3x20，且双曲线过点M(8,6、3)【总结升华】双曲线22%-首=1(a0,b0)的渐近线方程为ab22y=1的渐近线方【解析】(1)解法当焦点在x轴上时，设

11、双曲线的方程为x2y2程为xayx；若双曲线的方程为b2x2m=1n2m、n0,0,焦点在x轴上，：0,由题意，得(一3)2(23/b2所以双曲线的方程为4x2【变式1】中心在原点,一个焦点在(0,3)，一条渐近线为，解得9,b2=44A.5x236381宀的双曲线方程是(I54436B.D.365413x281比136【答案】当焦点在y轴上时,设双曲线的方程为【变式2】过点(2,-2)2且与双曲线2y2=1有公共渐近线的双曲线是()由题意，得(273)2(3)2，解得a2=-4,b2b2=19(舍去)综上所得，双曲线的方程为竺9A.2y22x4=1B22C.yx=1D42【答案】A=1解法二

12、：设所求双曲线方程为91622【变式3】设双曲线笃-丿1(a0)的渐近线方程为3x_2y=0，则a的值为a9将点(-3,2、一3)代入得所以双曲线方程为9164x22丄=14A.4B.3C.2【答案】C2D.1(2)依题意知双曲线两渐近线的方程是-23故设双曲线方程为49点M(8,6.3)在双曲线上,82(6、3)22x【变式4】双曲线二ab2x2(-=0)有相同的(A.实轴B.焦点C.渐近线D.以上都不对【答案】C类型三：求双曲线的离心率或离心率的取值范围22xy例4.已知F1,F2是双曲线一21(ab0)的左、右焦点，过F1且垂直于x轴的直线与双曲线的左支ab交于A、B两点，若ABF2是正

13、三角形,求双曲线的离心率。【解析I：IFE2c,.ABF2是正三角形,【总结升华】求双曲线的方程，关键是求a、b，在解题过程中应熟悉各元素(a、b、c、e及准线)之-|ARF2ctan30：=c,|AF2F2ctan303cos30所求双曲线方程为-丿=1.1636间的关系，并注意方程思想的应用。若已知双曲线的渐近线方程ax_by=0，可设双曲线方程为举一反三:-(IAF2I|BF2|)-(|AFi|BFi|)=12.【总结升华】双曲线的离心率是双曲线几何性质的一个重要参数，求双曲线离心率的关键是由条件寻求a、即(|AF2|BF2|)-|AB|=12c满足的关系式，从而求出|AF2|BF2|=

14、12|AB|=20.举一反三:【变式1】故.ABF2的周长L=|AF2I|BF2|IAB|=28.已知双曲线x2a2b2y=1(a0,b0)的离心率e=3,3【总结升华】双曲线的焦点三角形中涉及了双曲线的特征几何量，在双曲线的焦点三角形中，经常运用正弦定理、余弦定理、双曲线定义来解题，解题过程中，常对定义式两边平方探求关系.过点A（O,-b）和B（a,O）的直线与原点间的距离为，求双曲线的方程2举一反三:求过点（-1,3），且和双曲线49=1有共同渐近线的双曲线方程【变式1】已知双曲线的方程22冷一召=1，点AB在双曲线的右支上，且线段AB经过双曲线的右焦点F2,ab2【答案】（1）刍一宀1|

15、AB|=m,F1为另一焦点，则ABF的周长为（22(2)273A.2a+2mB.4a+2mC.a+mD.2a+4m【答案】B【变式2】（2015山东文）过双曲线C:令-a22x每=1（a0,b0）的右焦点作一条与其渐近线平行的直线,aX2【变式2】已知FpF2是双曲线92y=1的两个焦点,16P在双曲线上且满足|PR|PF2h32，则交C于点P.若点P的横坐标为2a,则C的离心率为f1pf2=【答案】2、3【答案】902【解析】双曲线2占=1的右焦点为（c,aa0）.不妨设所作直线与双曲线的渐近线Ky二一x平行，其方a【巩固练习】、选择题程为y=b(x-c)，代入x-aa2222a十ca十c2

16、二1求得点P的横坐标为x,由a22c2c=2a，得1.（2015广东）已知双曲线5的离心率e=-4，且其右焦点为F2（5,0）,则双曲线C的方解之得c=2+J3,c=2-J3（舍去，因为离心率c1）,故双曲线的离心率为ac分别为双曲线的实半轴长、虚半轴长、半焦距，且方程程为（）aa【变式3】已知a、b、ax2+bx+c=0无实根，则双曲线离心率的取值范围是x2191622191622x14A.1eJ52B.1e2C.1e3D.1e0,b0)的焦点到渐近线的距离是其顶点到渐近线距离的天津文)已知双曲线B.D.垂直，则双曲线的方程为(2xA.y42=1C.3xL3=1205二、填空题7.已知双曲线

17、C:3倍，则双曲线的y=3xB.D.-1(a0,b0)的焦距为25，且双曲线的一条渐近线与直线22丄=14223x3y=1520-22笃-召=1(a0,b0)的实轴长为2，离心率为2，则双曲线abC的焦点坐标是x2&椭圆42y2=1与双曲线a2x22-y=1焦点相同，贝Ua=a9.（2015春2黑龙江期末改编)与双曲线X2-y=1有共同的渐近线，且过点(42,2)的双曲线方程为_10.（2016浙江文)设双曲线x2-1的左、右焦点分别为Fi,F2.若点3P在双曲线上，且F1PF2为锐角三角形，则|PF|+|PF的取值范围是三、解答题2211.设F1,F2分别为双曲线22=1(a0,b0)的左、

18、右焦点.若在双曲线右支上存在点P,满足abPF2=F1F2，且F2到直线PF的距离等于双曲线的实轴长，求该双曲线的渐近线方程.22xy12.设双曲线二2=1(0a0,b0)过点AG145),且点A到双曲线的两条渐近线的距离的积为-3y2二1的两个焦点分别为F1、F2，点P在双曲线上且满足.F1PF2二90，求厶F1PF2的面积.22xy15.如下图，已知F1,F2是双曲线2=1(a0,b0)的两焦点，以线段FF2为边作正三角形MFF2,若ab边MF的中点在双曲线上，求双曲线的离心率.【答案与解析】1.【答案】：C【解析】由双曲线右焦点为222cb=ca=9,所以双曲线方程为2.答案】c5F2（

19、5,0），则Sa=42x162y=19|PF1|-|PF2|=2a,（不妨设该点在右支上）|PF1|+|PF2|=3b,所以|PF1|=2a3b【解析】：由双曲线的定义得:故e二总，故选B。33.答案】：D9222c5ab。结合c二ab得4a3【解析】：设双曲线方程为y2-x=(0)焦点（0,_4.3）,2,0)0,又2、=(43)2,，=244.【答案】：B【解析】：因为|PF2|=|F2F1I,P点满足b2卄2222cc-a,即2ac=b=c-a,a12=e,故e=1+2.e5.【答案】：B【解析】：如图，10.【答案】（2,7,8）耸=1,二y=卫Jc2a2ba分别过双曲线的右顶点A,右

20、焦点F作它的渐近线的垂线，B、C分别为垂足，则0BMAOCFOAABFCOFac_3一2&,a故渐近线方程为：y二22x.6.【答案】：Ab122【解析】由题意得c=-、5,=a=2,b=1=，xy1，选aa2417.【答案】：（土2,0）【解析】：由题意得:a=1,e=2,所以c=2,又由标准方程可得焦点在x轴上，所以焦点坐标为（土a&【答案】：2【解析】；由题意得4a2=a2+1,9.【答案】：22x-y=13122【解析】设双曲线方程为x2y-k2a2=3,a=62因为双曲线过点（2,2），所以k=3,所以双曲线的方程为22xy1。312.c【解析】由已知a=1,b=3,c=2，则e2,

21、设p（x,y）是双曲线上任一点，由对称性不妨设aP在右支上，贝U1vxv2,|PF1|=2x+1,|PF2|=2x1,/F1PF2为锐角,则|PF1|2+|PF2|2IF1F2I2，即(2x+1)2+(2x1)242，解得x7,所以辽X：:2,22|PFJIPF2h4x(2.7,8)11.【解析】：过F2作F2A丄PF于A,由题意知F2A=2a,=2a,4b2c=2a,c=2ba,22c=(2ba),a2+b2=4b24ab+a2,解得-a3双曲线的渐近线方程为12.【解析】：由已知，丨的方程为ay+bx-ab=0,原点到1的距离为卡,则一I/.34F1F2=2c,则AF|=2b,PR=4b,

22、而PF1PF2又c2=a2+b2,4ab=、3c2,两边平方，得2/22、小416a(c-a)=3c.两边同除以/0ab,2e=4,故a4并整理得3e4-16e2+16=0,.e2=4或e2=(3-1,21,得e2a一e=2.a2b22双曲线三-a点A到两渐近线的距离分别为|V14b+J5a|V14b_J5a13.【解析】2b2=1的两渐近线的方程为bxay=0.d1一,d21.a2b2222ab4,|14b-5a214.、已知d1d2=,故22(1)3a2+b23又A在双曲线上，则222214b5a=ab(ii)(ii)代入(1),得3a2b2=4a2+4b2(iii)a2b2x2_1)4)

23、，联立（ii）、（iii）解得b=2,a=4.22故所求双曲线方程为1.4214.【解析】：解法一：由双曲线的方程知a=2,b=1,c5因此|RF2|=2c=2.5.由于双曲线是对称图形，如图所示,设P点坐标为（x.由已知FF丄F2P,得x2=，SF1PF21吋2丨1X-12角1=15122V42V51 22解法二：/(|PF1|-|PF2|)=4a=16,又由勾股定理得|PF1|2+|PF1|2=(2c)2=20,22212 IPF1IIPF2|=|PF1|+IPF2I-(|PF1|-|PF2|)=(20-16)=2,2 SF1PF2T.15.【解析】：设MF的中点为P,在RtPMF中,|PF2|=IMFsin60=2cc.又由双曲线的定义得|PB|-1PF|=2a,所以a.3-1cc,e=2a