电子陶瓷教学课件04conductivity

《电子陶瓷教学课件04conductivity》由会员分享，可在线阅读，更多相关《电子陶瓷教学课件04conductivity（40页珍藏版）》请在装配图网上搜索。

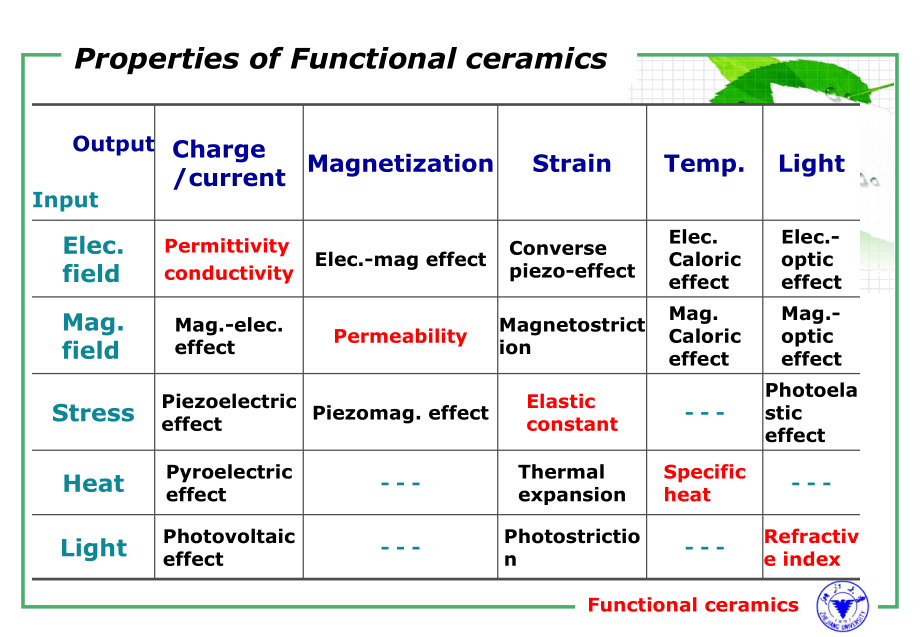
1、Functional ceramicsProperties of Functional ceramicsOutputInputCharge /currentMagnetizationStrainTemp.LightElec. fieldPermittivityconductivityElec.-mag effectConverse piezo-effectElec. Caloric effectElec.-optic effectMag. fieldMag.-elec. effectPermeabilityMagnetostrictionMag. Caloric effectMag.-opti

2、c effectStressPiezoelectric effectPiezomag. effectElastic constant- - -Photoelastic effectHeatPyroelectric effect- - - Thermal expansionSpecific heat- - - LightPhotovoltaic effect- - -Photostriction- - -Refractive indexFunctional ceramics3 Electrical ConductionThe electrical conduction characteristi

3、cs of ceramics can range from those of superconductors through those of metals to those of the most resistive of materials; in between the extremes are characteristics of semiconductors and semiinsulators. Conductivity of the various classed of material: shading indicates the range of values at room

4、 temperatures.Functional ceramicsConductivities of some typical ceramics room temperatureCeramicsConductivity（S/cm）CeramicsConductivity（S/cm）YBa2Cu3O7-d dSuperconductorBaTiO310-10SnO2-CuO103TiO2(rutile)10-11SiC10-1a a-Al2O310-14LaCrO310-23 Electrical ConductionFunctional ceramics3 Electrical Conduct

5、ionCeramicsMeasurement of conductivityElectrodesInner diameter D2, cmDiameter D1, cmThickness h, cmVolume conductivityhDRVV421Surface conductivity12ln2DDSSRFunctional ceramics3 Electrical ConductionMaterials classExampleConductivity levelCarrier typeSuperconductorsYBa2Cu3O7-d dInfiniteConductorsAg,

6、CuHighElectronsSrRuO3Electrons/IonsSemiconductorsSi, GeIntermediateElectronsZnOElectrons/IonsSemiinsulatorsZrO2IntermediateIons/ElectronsInsulatorAl2O3Very lowIons/ElectronsConductivity characteristics of the various classes of materialsFunctional ceramicsCarrier type:Metal ElectronsSemiconductor El

7、ectrons,holesCeramic Electrons, holes, ions3 Electrical Conduction陶瓷材料的导电机理非常复杂，在不同的温度范围，载流子的陶瓷材料的导电机理非常复杂，在不同的温度范围，载流子的种类可能不同。例如，刚玉种类可能不同。例如，刚玉(a a-Al2O3)陶瓷在低温时为杂质离子陶瓷在低温时为杂质离子电导，高温电导，高温(超过超过1100oC)时则呈现有明显的电子电导。时则呈现有明显的电子电导。Functional ceramicsCarrier typeExamplesElectronsZnO, TiO2, Al2O3，MnO2，SnO2,

8、 Fe3O4HolesCu2O, Ag2O, Hg2O, MnO, Bi2O3, Cr2O3IonsZrO2Electrons and holesSiC, Co3O4, Al2O3Carrier types of functional ceramics3 Electrical ConductionFunctional ceramicsElectronic conduction: electrons, holes, (band conduction)Polarons, (polaron conduction)Ionic conduction: ionsBand conduction3 Elect

9、rical ConductionFunctional ceramicsBand conductionSchematic electron energy band structures for (a) a metallic crystal and (b) a semiconducting or insulating crystal.3 Electrical ConductionFunctional ceramicsBand conductionBand structure with electrons promoted from the valence to the conduction ban

10、d. kTEBg2exp Temperature dependence of conductivity in band conduction:(2.3)3 Electrical ConductionFunctional ceramics3 Electrical ConductionThe theory outlined above was developed for group IV semiconducting elements such as silicon and germanium; some of the compounds of group III and V elements,

11、the III-V compounds, are also covalently bonded and have similar electrical properties which can be described in terms of a band model. The same model can be applied to an ionic solid. In this case, for the example of MgO: an electron in the conduction band derived from the Mg2+ 3s states and a hole

12、 in the valence band derived from the 2p states of the O2- ion. (Eg= 8 eV)Apart from the wider band gaps, electrons and holes in ionic solids have mobilities several orders lower than those in the covalent semiconductors. This is due to the variation in potential that a carrier experiences in an ion

13、ic lattice. Functional ceramicsOne of the most important features of oxide semiconductors is the effect on their behaviour of the external oxygen pressure.Conductivity of undoped BaTiO3 (Ba/Ti=1.000) as a function of pO2 and T. (After Smyth)3 Electrical ConductionFunctional ceramicsPolaron conductio

14、nIn some oxides, the electron and hole is regarded as “hopping” from site to site. “Hopping” conduction occurs when ions of the same type but with oxidation differing by unity occur on equivalent lattice sites and is therefore likely to be observed in transition metal oxides.For example:The addition

15、 of Li2O to NiO (fired under oxidizing conditions).The lithium ion Li+ (74pm) substitutes for the nickel ion Ni2+ (69pm), for every added Li+ one Ni2+ is promoted to the Ni3+ state, the lost electron filling a state in the oxygen 2p valence band.The lattice now contains Ni2+ and Ni3+ ions on equival

16、ent sites and is the model situation for conduction by polaron hopping, which is more often referred to simply as electron hopping. 3 Electrical ConductionFunctional ceramicsDifference between polaron conduction and band conduction:In polaron conduction, the concentration of carriers is determined s

17、olely by the doping level and is therefore temperature independent, whereas the carrier mobility is temperature activated:Resistivity of NiO as a function of lithium content. kTA expThus it follows that the temperature dependence of conductivity is similar to that for band conduction, but for differ

18、ent reasons.(2.4)3 Electrical ConductionFunctional ceramicsIonic conductionEnergy barriers to ionic transport in a crystal (a) in the absence of a field and (b) with applied field E. kTEiexp0 Temperature dependence of conductivity in ionic conduction:(2.5)3 Electrical ConductionFunctional ceramicsIo

19、nic conductionExtrinsic and intrinsic regimes in the log versus 1/T relation.Vacancies might also be introduced into the crystal extrinsically by the addition of impurities. High temperature: intrinsicto create and to move defectsLow temperature: extrinsiconly to move defects3 Electrical ConductionF

20、unctional ceramicsIonic conduction in glassesGlass formers: SiO2, B2O3, Al2O3Modifier ions: Li+, Na+, K+ (very mobile)Ca2+, Mg2+ (block the network)Observations:1. Conductivity depends upon temperature through an exponential term, because mobile need to be activated to squeeze their way past oxygen

21、ions in moving from one site to the next.2. For a given temperature and alkali ion concentration, decreases as the size of the mobile ion increases (e.g. Li+ Na+ K+, where the corresponding sizes of the three ion types are in the ratio 1:1.5:2).3. For a given temperature and mobile ion content, decr

22、eases as the concentration of blocking ions (Ca2+, Mg2+) increasing. kTEiexp0 3 Electrical ConductionFunctional ceramicsSummaryElectronic conductors (semiconductors), ionic conductors (solid electrolytes) and mixed electronic-ionic conductors are encountered in ceramics.In all cases the conductivity

23、 is likely to vary with temperature according to kTEaexp0 Ea, activation energyk, Boltzmann constantT, temperature(2.6)3 Electrical ConductionFunctional ceramicsMaterialsEaIntrinsic semiconductorHalf the band gapn-type extrinsic semiconductorHalf the gap between the donor level and the bottom of the

24、 conduction bandp-type extrinsic semiconductorHalf the gap between the acceptor level and the top of the valence bandCrystalline ionic conductor (pure)Energy to form defects together with the energy to move themCrystalline ionic conductor (doped)Energy to move the defectsGlass phaseEnergy to activat

25、e an ion to move from one lattice site to an adjacent siteChalcogenide glassesEnergy to activate the electron hopping processing3 Electrical ConductionFunctional ceramics4 Charge displacement processesWhen an electric field is applied to an ideal dielectric material there is no long-range transport

26、of charge but only a limited rearrangement such that the dielectric acquires a dipole moment and is said to be polarized. Atomic polarization , which occurs in all materials, is a small displacement of the electrons in an atom relative to the nucleus; in ionic materials there is, in addition, ionic

27、polarization involving the relative displacement of cation and anion sublattices.4.1. Dielectric in static electric fields4.1.1 macroscopic parametersFunctional ceramicsAtomic polarization and ionic polarization4 Charge displacement processesFunctional ceramicsDipolar materials, such as water, can b

28、ecome polarized because the applied electric field orients the molecules.Space charge polarization involves a limited transport of charge carriers until they are stopped at a potential barrier, possibly a grain boundary or phase boundary. 4.1.1 macroscopic parameters4 Charge displacement processesFu

29、nctional ceramicsDipolar polarization and space charge polarization4 Charge displacement processesFunctional ceramicsThe role of the dielectric in a capacitor.In situation (a) (separated by a vacuum) 0 EElectric field4 Charge displacement processesFunctional ceramicsIn situation (b) (with a dielectr

30、ic) 0EpT Electric fieldPED 0 Dielectric displacement vector(2.8)(2.9)4 Charge displacement processesFunctional ceramicswhere the dimensionless constant c ce is the electric susceptibility. In general, c ce is a tensor of the second rank. Unless otherwise stated it will be assumed in the following di

31、scussions that P and E are collinear, in which case c ce is simply a scalar.EEEDee000)1( c c c c It follows from (2.9) and (2.10) thatEPe0 c c If the dielectric is linear(2.10)(2.11)4 Charge displacement processesFunctional ceramicshUAQeT0)1( c c hAUQCeT0)1( c c In which QT is the total charge on th

32、e capacitor plate. Therefore the capacitor is Since D= T,The capacitor C0 of an empty parallel-plate capacitor is hAC00 (2.12)(2.13)(2.14)4 Charge displacement processesFunctional ceramics)1(0ec c re c c 10Where If the space between the plates is filled with a dielectric of susceptibility c ce, the

33、capacitor is increased by a factor 1+c ce and r is the relative permittivity (or dielectric constant) of the dielectric.(2.15)(2.16)4 Charge displacement processesFunctional ceramicsThe local field in a dielectric 4.1.2 From induced elementary dipoles to macroscopic propertiesEa applied external fie

34、ldEm internal macroscopic field Edp depolarizing fielddpamEEE (2.17)4 Charge displacement processesFunctional ceramicsAn individual atom or ion in a dielectric is not subjected directly to an applied field but to a local field EL, which has a very different value.Local field EL differs from Em since

35、 the latter is arrived at by considering the dielectric as a continuum.In reality the atomic nature of matter dictates that the local field, which is also known as the Lorentz field, must include contributions from the adjacent, individual dipoles. Furthermore, the local field arises from the charge

36、s in their displaced positions, and because it is also doing the displacing, calculation of it is by no means straightforward. 4 Charge displacement processesFunctional ceramicsLorentz calculated EL in the following way.Ep can be shown to be P/3 0, but Ed must be calculated for each particular site

37、chosen and for each dielectric material. dpmLEEEE In which Ep is the contribution from the charges at the surface of the spherical cavity (imaging for the moment that the sphere of material is removed) and Ed is due to the dipoles within the boundary. (2.18)4 Charge displacement processesFunctional

38、ceramics0033 PEEPEEdpamL For certain crystals of high symmetry and glasses it can be shown that Ed=0, and so for these casesIn which g g is the internal field constant.In the more general case it is assumed that PEEmLg g (2.19)4 Charge displacement processesFunctional ceramicsLEpa a )(PENNpPmg ga a

39、The dipole moment p induced in the entity can now be written If it is assumed that all entities are of the same type and have a density N, thenIn which a a is the polarizability of the entity, i.e. the dipole moment induced per unit applied field. oragag a ac c NNEPem 100(2.20)(2.21)(2.22)4 Charge d

40、isplacement processesFunctional ceramics0321 a a Nrr In the particular case for which g g=1/3 0 rearrangement of the previous equation leads to the Clausius-Mosottie relationship.Using the cgs system the Clausius-Mosottie relationship becomes(2.23)3/4)2/()1(cgsrrNa a (2.24)This form has been widely

41、used in calculating polarizabilities.4 Charge displacement processesFunctional ceramicsFor equation c ce as Nagag1, and this implies that under certain conditions lattice polarization produces a local field which tends to stabilize the polarization further a feedback mechanism. This points to the po

42、ssibility of spontaneous polarization, i.e. lattice polarization in the absence of an applied field.(a) Non-polar array; (b), (c) polar arrays. The arrows indicate the direction of spontaneous polarization Ps.agag a ac c NNEPem 1004 Charge displacement processesFunctional ceramicsSuch spontaneously

43、polarized materials do exist, ferroelectrics constitute an important class among them. Ferroelectric behaviour is limited to certain materials and to particular temperature ranges for a given material. Of the 32 crystal classes, 11 are centrosymmetric and non-piezoelectric. Of the remaining 21 non-c

44、entrosymmetric classes, 20 are piezoelectric and of these 10 are polar. 4 Charge displacement processesFunctional ceramicsLocal2.2 Charge displacement processesA limited number of pyroelectric materials have the additional property that the direction of the spontaneous polarization can be changed by

45、 an applied electric field or mechanical stress. Where the change is primarily due to an electric field the material is said to be ferroelectric; when it is primarily due to a stress it is said to be ferroelastic. The piezoelectric crystals are those that become polarized or undergo a change in pola

46、rization when they are stressed; conversely, when an electric field is applied they become strained. The 10 polar crystal types are pyroelectric as well as piezoelectric because of their spontaneous polarization. In a pyroelectric crystal a change in temperature produces a change in spontaneous pola

47、rization. Functional ceramicsLocal2.2 Charge displacement processeswhere A is a constant for a given material and q qc is a temperature near to but not identical with the Curie point Tc. Ferroelectrics possess very high permittivity values which vary considerably with both applied field strength and

48、 temperature. The permittivity reaches a peak at the Curie point and falls off at higher temperatures in accordance with the Curie-Weiss lawcrTAq q Functional ceramicsLocal2.2 Charge displacement processesBecause a ceramic is composed of a large number of randomly oriented crystallites it would norm

49、ally be expected to be isotropic in its properties. The possibility of altering the direction of the spontaneous polarization in the crystallites of a ferroelectric ceramic (a process called poling) makes it capable of piezoelectric, pyroelectric and electro-optical behaviour. The poling process the application of a static electric field under appropriate conditions of temperature and time aligns the polar axis as near to the field direction as the local environment and the crystal structure allow.Poling processY.J. WuY.J. Wu