机械优化设计第二五讲

《机械优化设计第二五讲》由会员分享，可在线阅读，更多相关《机械优化设计第二五讲（52页珍藏版）》请在装配图网上搜索。

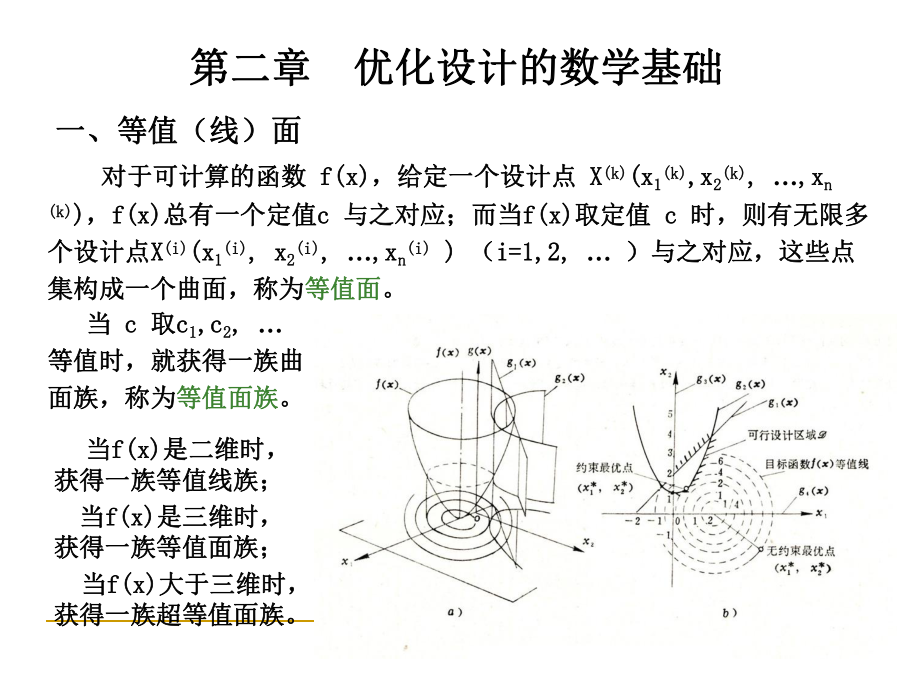
1、第二章第二章 优化设计的数学基础优化设计的数学基础一、等值（线）面一、等值（线）面 对于可计算的函数对于可计算的函数 f(x)f(x)，给定一个设计点，给定一个设计点 X X(k)(k)(x(x1 1(k)(k),x,x2 2(k)(k), , ,x,xn n (k)(k) )，f(x)f(x)总有一个定值总有一个定值c c 与之对应；而当与之对应；而当f(x)f(x)取定值取定值 c c 时，则有无限多时，则有无限多个设计点个设计点X X(i)(i)(x(x1 1(i)(i), x, x2 2(i)(i), , ,x,xn n(i)(i) ) ) （i=1,2, i=1,2, ）与之对应，这

2、些点）与之对应，这些点集构成一个曲面，称为集构成一个曲面，称为等值面等值面。 当当 c c 取取c c1 1,c,c2 2, , 等值时，就获得一族曲等值时，就获得一族曲面族，称为面族，称为等值面族等值面族。 当当f(x)f(x)是二维时，是二维时，获得一族等值线族；获得一族等值线族； 当当f(x)f(x)是三维时，是三维时，获得一族等值面族；获得一族等值面族； 当当f(x)f(x)大于三维时，大于三维时，获得一族超等值面族。获得一族超等值面族。等值线的等值线的“心心” （以二维为例）第二章第二章 优化设计的数学基础优化设计的数学基础 一个一个“心心”：是单峰函数的极（小）值点，是全局极（小）

3、值是单峰函数的极（小）值点，是全局极（小）值点。点。 没有没有“心心”：例，线性函数的等值线是平行的，无例，线性函数的等值线是平行的，无“心心”，认，认为极值点在无穷远处。为极值点在无穷远处。 多个多个“心心”：不是单峰函数，每个极（小）值点只是局部极不是单峰函数，每个极（小）值点只是局部极（小）值点，必须通过比较各个极值点和（小）值点，必须通过比较各个极值点和“鞍点鞍点”（须正确判别）（须正确判别）的值，才能确定极（小）值点。的值，才能确定极（小）值点。第二章第二章 优化设计的数学基础优化设计的数学基础等值线的分布规律等值线的分布规律： 等值线越内层其函数值越小（对于求目标函数的极小化来说）

4、等值线越内层其函数值越小（对于求目标函数的极小化来说） 沿等值线密的方向，函数值变化快；沿等值线疏的方向，函数值变沿等值线密的方向，函数值变化快；沿等值线疏的方向，函数值变化慢。化慢。 对于有心的等值线来说，其等值线簇的中心就是一个相对极小点；对于有心的等值线来说，其等值线簇的中心就是一个相对极小点；而对于无心的等值线簇来说，其相对极小点就是在无穷远了。而对于无心的等值线簇来说，其相对极小点就是在无穷远了。第二章第二章 优化设计的数学基础优化设计的数学基础二、梯度二、梯度方向导数：函数值在某一个方向的变化率。方向导数：函数值在某一个方向的变化率。 二维问题中，二维问题中，f (xf (x1 1

5、,x,x2 2 ) ) 在在 X X(0) (0) 点点沿方向沿方向 s s的方向导数为：的方向导数为：22)0(11)0()0(cos)(cos)()(xxfxxfsxf(0)(0)(0)(0)1212()()coscos,=() =()cos,Tf xf xSf xf xSf Sxx，其中：其中：Txxfxxfxf2)0(1)0()0()(,)()(是是 X X(0)(0)点的梯度。点的梯度。S S 为为s s方向的单位向量，方向的单位向量， 。1coscos2212S 为为 S S 的方向角的方向角, ,21,方向导数方向导数sf为梯度为梯度 在方向在方向 s s 上的投影。上的投影。第

6、二章第二章 优化设计的数学基础优化设计的数学基础梯度的性质：梯度的性质： 梯度的模因点而异，即函数梯度的模因点而异，即函数f(x)f(x)在不同点的最大增长率不同。在不同点的最大增长率不同。 梯度方向是梯度方向是X X(0)(0)点处指向函数变化率最大的方向，是函数的一点处指向函数变化率最大的方向，是函数的一种局部性质，只反映种局部性质，只反映X X(0)(0)点邻近的函数性质；点邻近的函数性质； 梯度方向与过该点的等值线的切线是正交的，是过该点的等值梯度方向与过该点的等值线的切线是正交的，是过该点的等值线的法线方向；线的法线方向； 正梯度方向是函数值最速上升的方向，负梯度方向是函数值最正梯度

7、方向是函数值最速上升的方向，负梯度方向是函数值最速下降的方向。速下降的方向。梯度方向的几何意义梯度方向的几何意义第二章第二章 优化设计的数学基础优化设计的数学基础梯度方向与等值线的关系梯度方向与等值线的关系第二章第二章 优化设计的数学基础优化设计的数学基础 对于对于 n n 维问题的梯度维问题的梯度Tnxxfxxfxxfxf )(,)(,)()()0(2)0(1)0()0(2)0(22)0(21)0()0()()()()(nxxfxxfxxfxf 第二章第二章 优化设计的数学基础优化设计的数学基础例例2-12-1求函求函数数 在在 处函数变化率最大的方向和数值。处函数变化率最大的方向和数值。5

8、24),(21222121xxxxxxfTx000解解 函数变化率最大的方向就是梯度方向，用单位向函数变化率最大的方向就是梯度方向，用单位向量量 表示，其数值就是梯度的模。计算如下：表示，其数值就是梯度的模。计算如下：p242242)(0021210 xxxxxfxfxf5224)(2222210 xfxfxf51525224)()(00 xfxfp第二章第二章 优化设计的数学基础优化设计的数学基础三、多元函数的泰勒展开三、多元函数的泰勒展开n n 维函数维函数 f(x) f(x) 在在 x x(k)(k) 点的泰勒展开式点的泰勒展开式: : njinjijikiniikkxRxxxxxfxx

9、xfxfxfk.)(!21)()(1,)(21)()()(二阶近似式：二阶近似式：)()()()()()()()(!21)()()(kkTkkTkkxxHxxxfxfxf其中：增量其中：增量 X (k) =x1 (k) , x2 (k) , xn (k) T梯度梯度 Tnkkkkxxfxxfxxfxf)(,.,)(,)()()(2)(1)()(Hesse Hesse 矩阵矩阵2222122222212212212212)(2)()(nnnnnkkxfxxfxxfxxfxfxxfxxfxxfxfxfxH第二章第二章 优化设计的数学基础优化设计的数学基础例例2-2 2-2 求二元函数求二元函数 在

10、在 点处的二阶泰勒展开式点处的二阶泰勒展开式 524),(21222121xxxxxxfTTxxx1220100解解 二阶泰勒展开式为二阶泰勒展开式为 )()(21)()(),(),(00000201021xxxHxxxxxfxxfxxfTT将将 的具体数值代入，有的具体数值代入，有 0 x0),(2010 xxf002242)(0021210 xxxxxfxfxf第二章第二章 优化设计的数学基础优化设计的数学基础2002)(02221222122120 xxfxxfxxfxfxH22212121202101020210121) 1()2(1220021221)(21),(xxxxxxxxxx

11、xHxxxxxxf此函数的图像是以此函数的图像是以 点为顶点的旋转抛物面。点为顶点的旋转抛物面。 0 x对于二次型函数，当对任何非零向量对于二次型函数，当对任何非零向量 使使0)(HxxxfTHx则二次型函数正定，则二次型函数正定， 为正定矩阵。为正定矩阵。四、四、Hesse Hesse 矩阵与正定矩阵与正定 由线性代数可知，对称矩阵正定的条由线性代数可知，对称矩阵正定的条件是它的行列式的顺序主子式全部大于零。件是它的行列式的顺序主子式全部大于零。第二章第二章 优化设计的数学基础优化设计的数学基础Hesse Hesse 矩阵的特性：是实对称矩阵。矩阵的特性：是实对称矩阵。 Hesse Hess

12、e 矩阵的正定性：矩阵的正定性：H(xH(x* *) )正定，正定， 是是 x x* * 为全局极小值点的充分条件为全局极小值点的充分条件；H(xH(x* *) )半正定半正定, , 是是 x x* * 为局部极小值点的充分条件；为局部极小值点的充分条件；H(xH(x* *) )负定，负定， 是是 x x* * 为全局极大值点的充分条件；为全局极大值点的充分条件；H(xH(x* *) )半负定半负定, , 是是 x x* * 为局部极大值点的充分条件。为局部极大值点的充分条件。 H H是正定矩阵的充要条件是它的所有主子式都大于是正定矩阵的充要条件是它的所有主子式都大于0;0; H H是负定矩阵

13、的充要条件是它的所有奇数阶主子式都小于是负定矩阵的充要条件是它的所有奇数阶主子式都小于0 0，并且它的所有偶数阶主子式都大于并且它的所有偶数阶主子式都大于0 0； H H是半正定矩阵的充要条件是它的所有主子式都大于等于是半正定矩阵的充要条件是它的所有主子式都大于等于0 0； H H是半负定矩阵的充要条件是它的所有奇数阶主子式都小于等是半负定矩阵的充要条件是它的所有奇数阶主子式都小于等于于0 0，并且它的所有偶数阶主子式都大于等于，并且它的所有偶数阶主子式都大于等于0 0；五、凸集、凸函数与凸规划五、凸集、凸函数与凸规划 设设 为为n n维设计空间中的一个集合，若其中任意两点维设计空间中的一个集

14、合，若其中任意两点 的连线都包含在该集合内，就称该集合是的连线都包含在该集合内，就称该集合是n n维设计维设计空间的一个凸集。空间的一个凸集。 R21xx 和第二章第二章 优化设计的数学基础优化设计的数学基础凸集具有以下性质：凸集具有以下性质： 1 1、若、若 是一个凸集，是一个凸集， 是一个实数，是一个实数， 是凸集是凸集 中中的动点，即的动点，即 ，则集合，则集合AAAaAaaxxA,:还是还是凸凸集。集。2 2、若、若 是凸集，是凸集， 分别是凸集分别是凸集 中的动点，中的动点，即即 ， ， 则集合则集合BA和ba、BA、AaBbBbAabaxxBA，,:还是凸集。还是凸集。3 3、任何

15、一组凸集的交集还是凸集。、任何一组凸集的交集还是凸集。 第二章第二章 优化设计的数学基础优化设计的数学基础 设设 为定义在为定义在n n维设计空间中一个凸集维设计空间中一个凸集 上的函数，上的函数，若对任何实数若对任何实数 及及 域中任意两点域中任意两点 存在如存在如下关系：下关系： 则称为则称为 定义在凸集定义在凸集 上的凸函数。上的凸函数。凸函数凸函数)(xfR) 10(R21xx 和)()1 ()()1 (2121xfxafxxf)(xfR 一元函数一元函数 若在若在aa，bb内为凸函数，其函数曲线上任内为凸函数，其函数曲线上任意两点所连的直线段不会落在曲线弧段以下，即函数值总是意两点所

16、连的直线段不会落在曲线弧段以下，即函数值总是小于或等于直线段上相应的纵坐标值。小于或等于直线段上相应的纵坐标值。)(xf第二章第二章 优化设计的数学基础优化设计的数学基础第二章第二章 优化设计的数学基础优化设计的数学基础凸函数的基本性质凸函数的基本性质：l 若若f(x)f(x)是定义在凸集是定义在凸集D D上的严格凸函数，则上的严格凸函数，则f(x)f(x)在在D D上的一个极小点，上的一个极小点， 也就是全局最小点。也就是全局最小点。l 凸函数的线性组合仍然为凸函数。凸函数的线性组合仍然为凸函数。l 设设x x(1)(1), x, x(2)(2)为凸函数为凸函数 f(x)f(x)上的两个最小

17、点，则其连线上的任意点也都上的两个最小点，则其连线上的任意点也都是最小点。是最小点。 凸性函数的判定（凸性函数的判定（判别函数为凸函数的条件）判别函数为凸函数的条件）l 按梯度判断凸性：设按梯度判断凸性：设f(x)f(x)是定义在凸集是定义在凸集 D D上具有连续一阶导数的函上具有连续一阶导数的函数，则数，则f(x)f(x)在在D D上为凸函数的充要条件是：对于任意的上为凸函数的充要条件是：对于任意的 x x(1)(1),x,x(2)(2)D D 都都有有 成立。成立。 l 按二阶偏导数判断凸性：设按二阶偏导数判断凸性：设 f(x) f(x) 是定义在凸集是定义在凸集D D上具有连续二阶导上具

18、有连续二阶导数的函数，则数的函数，则f(x)f(x)在在D D上为凸函数的充要条件是：上为凸函数的充要条件是：f(x)f(x)的的HesseHesse矩阵处处矩阵处处半正定。若半正定。若HesseHesse矩阵处处正定，则矩阵处处正定，则f(x)f(x)为严格凸函数。为严格凸函数。)()()()1()2()1()1()2(xxxfxfxfT)(pf目标函数是非凸函数（图目标函数是非凸函数（图 a a），或可行域是非凸集（图），或可行域是非凸集（图 b b）：）： 则目标函数等值线与适时约束曲面可能存在多个切点，则目标函数等值线与适时约束曲面可能存在多个切点，是局部极值点，其中只有一个点是全局最

19、优点。是局部极值点，其中只有一个点是全局最优点。p)(pg)(qf)(qg)(pf)(qf)(pg)(qgQQp第二章第二章 优化设计的数学基础优化设计的数学基础凸规划凸规划 对于约束优化问题对于约束优化问题 mjxgxfj, 2 , 10)(. .)(min 若若 、 都为凸函数，则称此问题都为凸函数，则称此问题为凸规划。为凸规划。 )(xfmjxgj, 2 , 10)( 1.1.若给定一点若给定一点 ，则集合，则集合 为凸集。此性质为凸集。此性质表明，当表明，当 为二元函数时其等值线呈现大圈套小圈形式。为二元函数时其等值线呈现大圈套小圈形式。 0 x)()(0 xfxfxR)(xf凸规划的

20、性质凸规划的性质第二章第二章 优化设计的数学基础优化设计的数学基础2. 2. 可行域可行域 为凸集。为凸集。 mjxgjxR, 2, 10)(3.3.凸规划的任何局部最优解就是全域最优解。凸规划的任何局部最优解就是全域最优解。 无约束优化问题是使目标函数取得极小值，无约束优化问题是使目标函数取得极小值，极值条件是指目标函数取得极小值时极值点应极值条件是指目标函数取得极小值时极值点应满足的条件。满足的条件。 对一元函数，取极值的必要条件是对一元函数，取极值的必要条件是0)(0 xf取极值的充分条件是在驻点附近，若取极值的充分条件是在驻点附近，若，则该点为极大点，若，则该点为极大点，若 ，则该点为

21、极小点。则该点为极小点。0)( 0 xf0)( 0 xf六六 无约束优化问题的极值条件无约束优化问题的极值条件 对二元函数，取极值的必要条件是对二元函数，取极值的必要条件是 00021xxxfxf为了判断从上述必要条件求得的是否为极值为了判断从上述必要条件求得的是否为极值点，需要建立极值的充分条件。根据二元函点，需要建立极值的充分条件。根据二元函数在点处的泰勒展开式，考虑上述极值必要数在点处的泰勒展开式，考虑上述极值必要条件，有条件，有0)(0 xf 222222121221212201021000221),(),(xxfxxxxfxxfxxfxxfxxx即即 此条件反映了此条件反映了 在在

22、点处的海森点处的海森矩阵矩阵 的各阶主子式均大于零，即对于的各阶主子式均大于零，即对于),(21xxf)(0 xH0 x 所以，二元函数在某点处取得极值的充分所以，二元函数在某点处取得极值的充分条件是要求在该点处的条件是要求在该点处的海森矩阵为正定。海森矩阵为正定。0)(*21* Txnxfxfxfxf极值的充分条件为极值的充分条件为 *2222122222212212212212*)(xnnnnnxfxxfxxfxxfxfxxfxxfxxfxfxH(2-7) 正定。正定。 依此类推，多元函数依此类推，多元函数 在在 点处取极值的必要条件为点处取极值的必要条件为 ),(21nxxxf 第二章第

23、二章 优化设计的数学基础优化设计的数学基础例例2-3 2-3 求函数求函数 的极值。的极值。524),(21222121xxxxxxf解解 首先，根据极值的必要条件求驻点。首先，根据极值的必要条件求驻点。002242)(0021210 xxxxxfxfxf得驻点为得驻点为 1220100 xxx再根据极值的充分条件，判断此点是否为极值点。由于再根据极值的充分条件，判断此点是否为极值点。由于第二章第二章 优化设计的数学基础优化设计的数学基础2002)(02221222122120 xxfxxfxxfxfxH的一阶主子式和二阶主子式分别为的一阶主子式和二阶主子式分别为020212xxf042002

24、)(0 xH故故 为正定矩阵为正定矩阵 为极小点，相应的为极小点，相应的极值为极值为 。)(0 xHTx2 , 100)(0 xf第二章第二章 优化设计的数学基础优化设计的数学基础无约束优化设计问题最优解：无约束优化设计问题最优解： 不受约束条件限制，使目标函数达到最小值的一组设计不受约束条件限制，使目标函数达到最小值的一组设计变量，即最优点变量，即最优点 x x* *=x=x1 1* *,x,x2 2* *, ,x,x n n* * 和最优值和最优值 f(xf(x* *) )构成构成无约束问题最优解。无约束问题最优解。 x x* *为无约束极小点的充要条件为无约束极小点的充要条件（1 1）

25、；(2)Hesse(2)Hesse矩阵矩阵 为正定。为正定。0)(*xf)(*xH第二章第二章 优化设计的数学基础优化设计的数学基础约束优化设计问题最优解约束优化设计问题最优解： 满足约束条件，使目标函数达到最小值的一组设计变量，满足约束条件，使目标函数达到最小值的一组设计变量， 即最优点即最优点 x x* *=x=x1 1* *,x,x2 2* *, ,x,x n n* * 和最优值和最优值 f(xf(x* *) )构成约束问构成约束问题最优解。题最优解。0)(0)(05 . 2)(. .41060)(min23122221121222121xxgxxgxxxgtsxxxxxxxf其中其中

26、是约束最优点，而是约束最优点，而 是无约束最优点。是无约束最优点。Tx3 , 4*Tx6 , 8*第二章第二章 优化设计的数学基础优化设计的数学基础等式约束优化问题的极值条件等式约束优化问题的极值条件 求解等式约束优化问题求解等式约束优化问题), 2 , 1(0)(. .)(minmkxhxfk 其思路就是将其转化成无约束优化问题，导出极值存在的其思路就是将其转化成无约束优化问题，导出极值存在的条件。数学上有两种处理方法：条件。数学上有两种处理方法：消元法和拉格朗日乘子法。消元法和拉格朗日乘子法。 约束优化问题可分为等式约束与不等式约束优约束优化问题可分为等式约束与不等式约束优化问题。化问题。

27、第二章第二章 优化设计的数学基础优化设计的数学基础消元法消元法 为了便于理解，先讨论二元函数只有一个等式约束的为了便于理解，先讨论二元函数只有一个等式约束的情况情况 0),(. .),(min2121xxhxxf用消元法求解就是根据等式约束条件，将一个变量表示成另用消元法求解就是根据等式约束条件，将一个变量表示成另一个变量的函数关系一个变量的函数关系 ，然后将其代入到目标函数，然后将其代入到目标函数 中消去中消去 ，变成一元函数，变成一元函数 ，从而将等式约束优化问题，从而将等式约束优化问题转化成无约束优化问题。目标函数通过消元由二元函数变成转化成无约束优化问题。目标函数通过消元由二元函数变成

28、一元函数，由二维变成一维。一元函数，由二维变成一维。 )(21xx1x)(2xF第二章第二章 优化设计的数学基础优化设计的数学基础对于对于 维情况维情况 n), 2 , 1(0),(. .),(min2121lkxxxhxxxfnkn 由由 个约束方程将个约束方程将 个变量中的前个变量中的前 个变量用其余个变量用其余 个个 变量表示，既有变量表示，既有 llnln),(),(),(2121222111nllllnllnllxxxxxxxxxxxx将这些函数关系代入到目标函数中去，得到只含将这些函数关系代入到目标函数中去，得到只含 共共 个变量的函数个变量的函数 ，从而可以利用无，从而可以利用无

29、约束优化问题的极值条件求解。约束优化问题的极值条件求解。 nllxxx,21ln),(21nllxxxF第二章第二章 优化设计的数学基础优化设计的数学基础拉格朗日乘子法拉格朗日乘子法 拉格朗日乘子法与消元法相反，是通过增加变量将等拉格朗日乘子法与消元法相反，是通过增加变量将等式约束优化问题转化成无约束优化问题。对于具有式约束优化问题转化成无约束优化问题。对于具有 个等个等式约束的式约束的 维优化问题。维优化问题。nl), 2 , 1(0)(. .)(minlkxhxfk 构造如下形式的新的目标函数：构造如下形式的新的目标函数： lkkkxhxfxF1)()(),(式中的式中的 就是原目标函数就

30、是原目标函数 的等式约束条件，而待定的等式约束条件，而待定系数系数 称为拉格朗日乘子称为拉格朗日乘子, , 称为拉格朗称为拉格朗函数。因为函数。因为 ，所以求，所以求 的极值就的极值就相当于求原目标函数相当于求原目标函数 的极值。这样就把求等式约束优化的极值。这样就把求等式约束优化问题转化成求有问题转化成求有l+nl+n个变量的无约束优化问题。由个变量的无约束优化问题。由 具有极值的必要条件具有极值的必要条件第二章第二章 优化设计的数学基础优化设计的数学基础)(xhk)(xf), 2 , 1(lkk),(xF), 2 , 1(0)(lkxhk ),(xF)(xf), 2 , 1(0), 2 ,

31、 1(0lkFnixFki可得可得l+n个方程，从而解得个方程，从而解得 和和共共l+n个未知变量的值。由上述方程组求得的个未知变量的值。由上述方程组求得的 是函是函数数 极值点的坐标值极值点的坐标值。), 2 , 1(lkk)(xfTnxxxx*2*1*,Tnxxxx,21第二章第二章 优化设计的数学基础优化设计的数学基础从上述分析过程可以看出求解等式约束优化问题，可通过把从上述分析过程可以看出求解等式约束优化问题，可通过把目标函数改造成如下形式的新的目标函数。目标函数改造成如下形式的新的目标函数。 lkkkxhxfxF1)()(),(从而将等式约束优化问题转化成无约束优化问题。从而将等式约

32、束优化问题转化成无约束优化问题。这种方法称为拉格朗日乘子法，可以叙述如下：这种方法称为拉格朗日乘子法，可以叙述如下：设优化问题设优化问题), 2 , 1(0),(. .),(min2121lkxxxhxxxfnkn 第二章第二章 优化设计的数学基础优化设计的数学基础为求出为求出 可能的极值点可能的极值点 ，引入拉，引入拉格朗日乘子格朗日乘子 ，并构成一个新的目标函数，并构成一个新的目标函数)(xfTnxxxx*2*1*,), 2 , 1(lkklkkkxhxfxF1)()(),(把把 作为一个新的无约束条件的目标函数来求它的极作为一个新的无约束条件的目标函数来求它的极值点，所得的结果就是满足约

33、束条件值点，所得的结果就是满足约束条件 的原目标函数的原目标函数 的极值点。的极值点。),(xF0),(21nkxxxh)(xf例例2-4 2-4 用拉格朗日乘子法计算约束条件为用拉格朗日乘子法计算约束条件为 和目标函数为和目标函数为 的极值点坐标。的极值点坐标。 0632),(2121xxxxh22212154),(xxxxf第二章第二章 优化设计的数学基础优化设计的数学基础解解 改造目标函数改造目标函数 )632(54),(212221xxxxxF063203100282111xxFxxFxxF解前两式得解前两式得 103,4121xx代入第三式得代入第三式得 ，因此得极值点，因此得极值点

34、 的坐标为的坐标为 730*x286. 1,071. 1*2*1xx第二章第二章 优化设计的数学基础优化设计的数学基础2.62.6不等式约束优化问题极值条件不等式约束优化问题极值条件mjxgxfj, 2 , 10)(. .)(min K-T ( Kuhn-Tucker K-T ( Kuhn-Tucker 库恩库恩- -塔克塔克) ) 条件条件2.6.1 2.6.1 一元不等式约束问题极值条件一元不等式约束问题极值条件12min( ). .( )=a-x0( )=x-b0f xg xgx 第二章第二章 优化设计的数学基础优化设计的数学基础1. 1. 有一个适时约束时：有一个适时约束时： 从数学上

35、定义，当从从数学上定义，当从 x x(k)(k)点出发点出发不不存在一个存在一个 S S 方向能同时满足：方向能同时满足： ; ; ，即，即 ， 则获得最优解：则获得最优解：x x(k)(k)为最优点为最优点 x x* *，f(xf(x(k)(k) )为最优值为最优值 f(xf(x* *) )。0)()(kTxfS0)()(kTxgS0),()()()(kkxgxf从几何上看，当从从几何上看，当从 x (k)x (k)点出发点出发不不存在一个存在一个 S S 方向能同时满足方向能同时满足： 与与x x(k)(k)点目标函数的负梯度方向成锐角，点目标函数的负梯度方向成锐角，即沿即沿 S S 方向

36、目标函数值下降；方向目标函数值下降； 与与x x(k)(k)点约束函数的梯度方向成钝角，即点约束函数的梯度方向成钝角，即保证保证 S S方向上各点在可行域内。方向上各点在可行域内。 此时，获得最优解此时，获得最优解 x x(k)(k) 为最优点为最优点 x x* *，f(xf(x(k)(k) )为最优值为最优值 f(xf(x* *) )。2.6.2 2.6.2 库恩库恩- -塔克条件（塔克条件（K-TK-T条件）条件）几何意义几何意义第二章第二章 优化设计的数学基础优化设计的数学基础 相反，当从相反，当从 x x(k)(k)点出发，存在一个点出发，存在一个 S S 方向能同时满足：方向能同时满

37、足： 和和 时，则时，则 x x(k)(k) 不是最不是最优点。优点。0)()(kTxfS0)()(kTxgS 从几何上看，当从从几何上看，当从 x x(k)(k)点出发存在一个点出发存在一个 S S 方向能同时满足：方向能同时满足： 与与x x(k)(k)点目标函数的负梯度方向成锐角，即点目标函数的负梯度方向成锐角，即沿沿 S S 方向目标函数值下降；方向目标函数值下降； 与与x x(k)(k)点约束函数的梯度方向成钝角，即保点约束函数的梯度方向成钝角，即保证证 S S方向上各点在可行域内。方向上各点在可行域内。 此时，此时，x x(k)(k)不是最优点不是最优点 x x* *。第二章第二章

38、 优化设计的数学基础优化设计的数学基础2. 2. 有二个适时约束时：有二个适时约束时： x x(k)(k)成为约束最优点成为约束最优点 x x* * 的必要条件为的必要条件为: :)()()()(22)(11)(kkkxgxgxf0, 021即不存在一个即不存在一个 S S 方向能同时满足：方向能同时满足：0)()(1kTxgS0)()(kTxfS0)()(2kTxgS 几何上几何上 位于位于和和 所张的扇形子空间所张的扇形子空间内。内。)()(kxf)()(1kxg)()(2kxg第二章第二章 优化设计的数学基础优化设计的数学基础相反，不符合以上条件：相反，不符合以上条件：不能表达成不能表达

39、成 和和 的线性组合。的线性组合。)()(kxf)()(1kxg)()(2kxg即存在一个即存在一个 S S 方向能同时满足：方向能同时满足：0)()(kTxfS0)()(1kTxgS0)()(2kTxgS几何上几何上 不位于不位于 和和 所张的扇形子空所张的扇形子空间内。则间内。则 x x(k)(k) 点不是最优点。点不是最优点。)()(kxf)()(1kxg)()(2kxg)()(kxf)()(2kxg)()(1kxg第二章第二章 优化设计的数学基础优化设计的数学基础 K-T K-T 条件（扩展至条件（扩展至 m m 个适时约束）：个适时约束）：,.,2 , 1, 0)()()()(mux

40、guxIkuk 设某个设计点设某个设计点 x x(k)(k)，其适时约束集为，其适时约束集为 且且 为线性独立，则为线性独立，则 x x(k)(k)成为约束最优点的必要条件是成为约束最优点的必要条件是目标函数的负梯度向量可表示为适时约束梯度向量的线性组合，目标函数的负梯度向量可表示为适时约束梯度向量的线性组合，即即 ，其中，其中 。 )(),()()(kkuxIuxg)()()()()()(kuxIuukxgxfk)(, 0)(kxIu 几何上，几何上，x x(k)(k)成为约束最优点成为约束最优点（极小点）（极小点）x x* *时，目标函数的时，目标函数的负梯度向量位于负梯度向量位于 m m

41、 适时约束梯适时约束梯度向量所张成的子空间内。度向量所张成的子空间内。第二章第二章 优化设计的数学基础优化设计的数学基础K-TK-T条件对于约束优化设计问题的重要性在于条件对于约束优化设计问题的重要性在于（1 1） 可以通过这个条件检验设计点可以通过这个条件检验设计点x x* *是否为约束是否为约束极小点，因此它可以成为某些迭代算法的一种收敛极小点，因此它可以成为某些迭代算法的一种收敛条件；条件；（2 2） 可以检验一种搜索方法是否合理，如果用这可以检验一种搜索方法是否合理，如果用这种迭代方法求得的最优点符合种迭代方法求得的最优点符合K-TK-T条件，则方法可以条件，则方法可以认为是可行的。认

42、为是可行的。第二章第二章 优化设计的数学基础优化设计的数学基础 3）构建方程组：按）构建方程组：按K-T条件，条件，x(k)点应满足点应满足 4）该方程组存在唯一解，解方程组得到一组乘子）该方程组存在唯一解，解方程组得到一组乘子 ， 若其中若其中 ，则点是约束极小点，否则不是约束极小点。，则点是约束极小点，否则不是约束极小点。 )()(kxf)()(kuxg( )( )( )jj 11()()()0Jlkkkjpppf xgxhxvJ,110u应用应用K-T条件检验某迭代点条件检验某迭代点x(k)是否为极值的具体步骤为：是否为极值的具体步骤为：1）找出可行点）找出可行点x(k)处的有效约束；处

43、的有效约束；2）计算计算x(k)点的目标函数梯度点的目标函数梯度 和有效约束函数的梯和有效约束函数的梯度度 ；第二章第二章 优化设计的数学基础优化设计的数学基础例例 试检验点试检验点 是否是下面不等式约是否是下面不等式约束优化问题束优化问题 的极小点。的极小点。 12, 00)2()1(xx042)(05)(0)(0)(. .)2()3()(min2142221322112221xxxgxxxgxxgxxgtSxxxf第二章第二章 优化设计的数学基础优化设计的数学基础第二章第二章 优化设计的数学基础优化设计的数学基础第二章第二章 优化设计的数学基础优化设计的数学基础第二章第二章 优化设计的数学

44、基础优化设计的数学基础习 题1 1、试求下列目标函数的无约束极值点，并判断它们是、试求下列目标函数的无约束极值点，并判断它们是极小点、极大点或鞍点。极小点、极大点或鞍点。522)()933)()10642)()22123)()1212222141122213231212221211212221xxxxxxxfdxxxxxxfcxxxxxxxfbxxxxxxfa第二章第二章 优化设计的数学基础优化设计的数学基础习 题2 2、优化问题、优化问题01)(0)(0)(. .)2)(min2221322112221xxxgxxgxxgtsxxxf（的一个数值解的一个数值解 ，试判定该解是否上述问题的优化，试判定该解是否上述问题的优化解。解。Tx01 ，