《上海八年级历年来期末考卷综合题(共15页)》由会员分享，可在线阅读，更多相关《上海八年级历年来期末考卷综合题(共15页)（15页珍藏版）》请在装配图网上搜索。
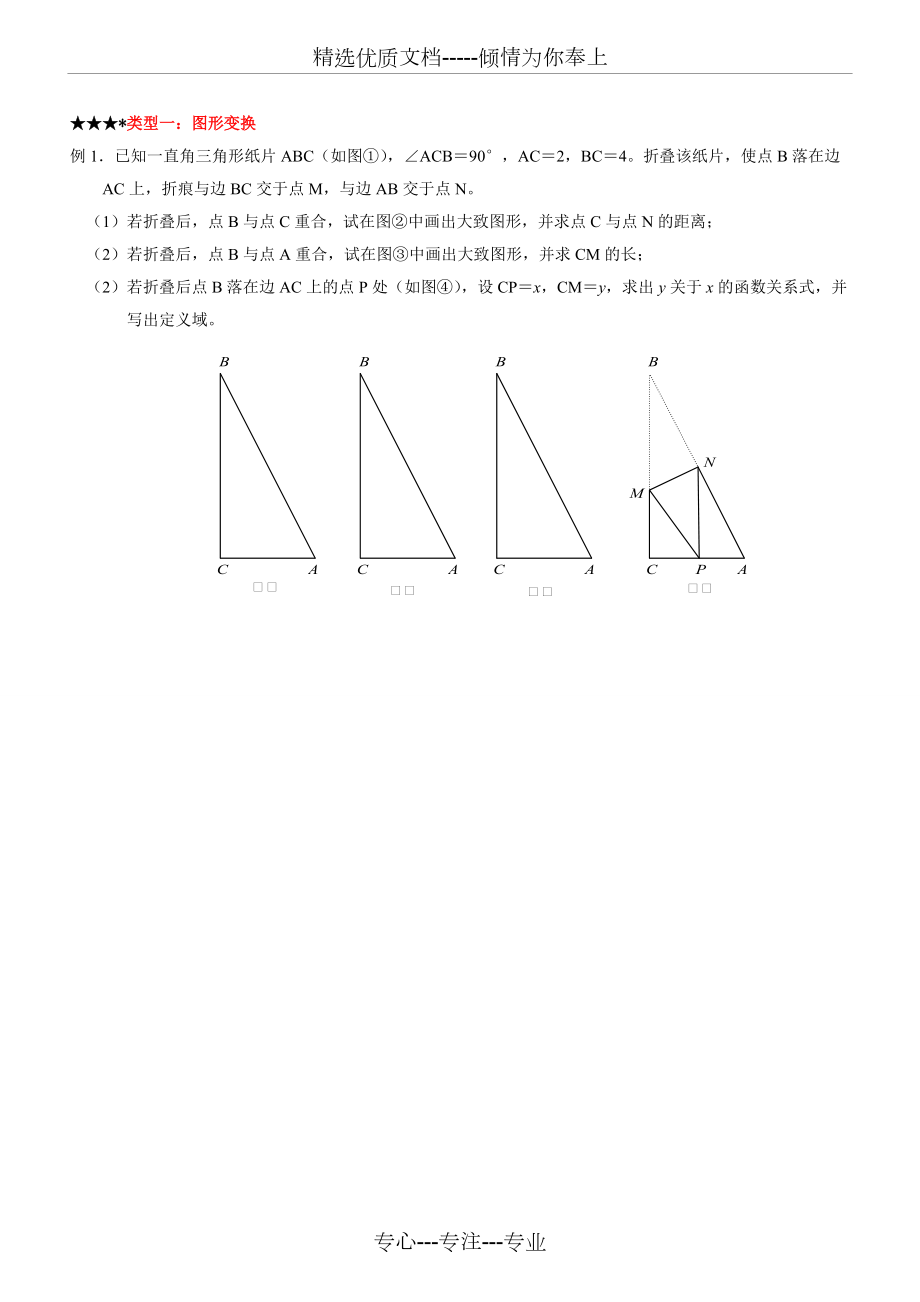
1、精选优质文档-倾情为你奉上 *类型一：图形变换例1已知一直角三角形纸片ABC（如图），ACB90，AC2，BC4。折叠该纸片，使点B落在边AC上，折痕与边BC交于点M，与边AB交于点N。（1）若折叠后，点B与点C重合，试在图中画出大致图形，并求点C与点N的距离；（2）若折叠后，点B与点A重合，试在图中画出大致图形，并求CM的长；（2）若折叠后点B落在边AC上的点P处（如图），设CPx，CMy，求出y关于x的函数关系式，并写出定义域。*【举一反三】1.小刘同学在一次课外活动中，用硬纸片做了两个直角三角形，见图1、图2图1中，；图2中，图3是小刘同学所做的一个实验：他将的直角边DE与的斜边AC重合
2、在一起，并将沿AC方向移动在移动过程中，D、E两点始终在AC边上（移动开始时点D与点A重合）（1）在沿AC方向移动的过程中，小刘同学发现：F、C两点间的距离逐渐_；（填“不变”、“变大”或“变小”）（2）小刘同学经过进一步研究，编制了如下问题： 问题：当移动至什么位置，即AD的长为多少时，F、C的连线与AB平行? 问题：当移动至什么位置，即AD的长为多少时，以线段AD、FC、BC的长度为三边长的三角形是直角三角形?ABC图1图2FDEABCFDE图3请你分别完成上述两个问题的解答过程2. 已知中，是边中点，将一块直角三角板的直角顶点放在点旋转，直角的两边分别与边交于。取运动过程中的某一瞬间，如
3、图，画出关于点的中心对称图形，的对称点为，试判断于的位置关系，并说明理由。设，求与的函数关系式，并写出定义域。3（12分）已知一直角三角形纸片OAB，AOB=90，OA=2，OB=4将该纸片放在平面直角坐标系中（如图），折叠该纸片，折痕与边OB交于点C，与边AB交于点D(1) 若折叠后使点B与O重合（如图），求点C的坐标及C、A两点的距离；(2) 若折叠后使点B与A重合（如图），求点C的坐标；(3) 若折叠后点B落在边OA上的点为B（如图），设OB= x，OC = y，求出y关于x的函数关系式，并写出定义域图图图D图*类型二：动点问题例1如图（1），直角梯形OABC中，A= 90，ABCO,
4、且AB=2，OA=2，BCO= 60。（1）求证：OBC为等边三角形；（2）如图（2），OHBC于点H，动点P从点H出发，沿线段HO向点O运动，动点Q从点O出发，沿线段OA向点A运动，两点同时出发，速度都为1/秒。设点P运动的时间为t秒，OPQ的面积为S，求S与t之间的函数关系式，并求出t的取值范围；（备用图）图(1)图(2)（3）设PQ与OB交于点M，当OM=PM时，求t的值。*【举一反三】1. 已知在ABC中，ACB90，ACBC，点D是AB上一点，AEAB，且AEBD，DE与AC相交于点F。（1）若点D是AB的中点（如图1），那么CDE是_三角形，并证明你的结论；（2）若点D不是AB的中
5、点（如图2），那么（1）中的结论是否仍然成立，如果一定成立，请加以说明，如果不一定成立，请说明理由；（3）若ADAC，那么AEF是_三角形。（不需证明）*类型三：函数与几何综合例1如图，直线经过原点和点，点B坐标为（1）求直线l所对应的函数解析式；（2）若P为射线OA上的一点，设P点横坐标为，OPB的面积为，写出关于的函数解析式，指出自变量x的取值范围当POB是直角三角形时，求P点坐标*【举一反三】1、已知：如图，正比例函数的图像与反比例函数的图像交于点(3,2)（1）试确定上述正比例函数和反比例函数的解析式；（2）根据图像回答：在第一象限内，当取何值时，反比例函数的值大于正比例函数的值?AM
6、BCODy（3）是反比例函数图像上的一动点，其中03，过点作直线轴，交轴于点；过点作直线轴交轴于点，交直线于点当四边形的面积为6时，请判断线段与的大小关系，并说明理由 2已知：如图，在RtABC中，A90，ABAC1，P是AB边上不与A点、B点重合的任意一个动点，PQBC于点Q，QRAC于点R。（1）求证：PQBQ；（2）设BPx，CRy，求y关于x的函数解析式，并写出定义域；（3）当x为何值时，PR/BC。4. 在直角三角形ABC中，C90，已知AC6cm，BC8cm。 （1）求AB边上中线CM的长；（2） 点P是线段CM上一动点（点P与点C、点M不重合），求出APB的面积y（平方厘米）与C
7、P的长x（厘米）之间的函数关系式并求出函数的定义域 （3）是否存在这样的点P，使得ABP的面积是凹四边形ACBP面积的，如果存在请求出CP的长，如果不存在，请说明理由！ 5. 如图，在长方形ABCD中，AB=8，AD=6，点P、Q分别是AB边和CD边上的动点，点P从点A向点B运动，点Q从点C向点D运动，且保持AP=CQ。设AP=，BE=y（1）线段PQ的垂直平分线与BC边相交，设交点为E求y与的函数关系式及取值范围；（2）在（1）的条件是否存在x的值，使PQE为直角三角形?若存在，请求出x的值，若不存在请说明理由。6如图，在中，=90，=30，是边上不与点A、C重合的任意一点，垂足为点，是的中
8、点.（1）求证：=； （2）如果=，设=，=，求与的函数解析式，并写出函数的定义域； （3）当点在线段上移动时，的大小是否发生变化？如果不变，求出的大小；如果发生变化，说明如何变化.7如图，已知长方形纸片ABCD的边AB=2，BC=3，点M是边CD上的一个动点（不与点C重合），把这张长方形纸片折叠，使点B落在M上，折痕交边AD与点E，交边BC于点F（1）、写出图中全等三角形；（2）、设CM=x，AE=y，求y与x之间的函数解析式，写出定义域；（3）、试判断能否可能等于90度？如可能，请求出此时CM的长；如不能，请说明理由*类型四：几何综合例1、 如图,已知中, BC=3, AC=4, AB=5
9、,直线MD是AB的垂直平分线，分别交AB、AC于M 、D点. DABMNC（1）求线段DC的长度；（2）如图（第27题图2），联接CM，作的平分线交DM于N .求证:CMMN .*【举一反三】1已知：如图，在ABC中，ADBC，垂足为D，BEAC，垂足为E，M是AB边的中点，联结MD、ME、ED.求证：(1) MED是等腰三角形；(2) EMD=2DAC.2 、在ABC中，ADBC，垂足为点D（D在BC边上），BEAC，垂足为点E，M为AB边的中点，联结ME、MD、ED。（1） 当点E在AC边上时（如图7），容易证明EMD=2DAC；当点E在CA的延长线上，请在图8中画出相应的图形，并说明“E
10、MD=2DAC”是否还成立？若成立，请证明；若不成立，请说明理由；ABCDEM（2） 如果MDE为正三角形，BD=4，且AE=1，求MDE的周长（图8）ABCD（图7）3.如图，RtABC中，AB=AC，O为BC中点。（1） 写出点O到ABC三个顶点的距离之间的关系；（2） 如果点M、N分别在边AB、AC上移动，且保持AN=BM。请判断OMN的形状，并证明你的结论。4.如图，在ABC中，C90，B30，AC6，点D、E、F分别在边BC、AC、AB上（点E、F与ABC顶点不重合），AD平分CAB，EFAD，垂足为H （1）求证：AEAF： （2）设CEx，BFy，求x与y之间的函数解析式，并写出定义域；（3）当DEF是直角三角形时，求出BF的长专心-专注-专业
上海八年级历年来期末考卷综合题(共15页)
