格林公式·曲线积分与线路的无关性

《格林公式·曲线积分与线路的无关性》由会员分享，可在线阅读，更多相关《格林公式·曲线积分与线路的无关性（25页珍藏版）》请在装配图网上搜索。

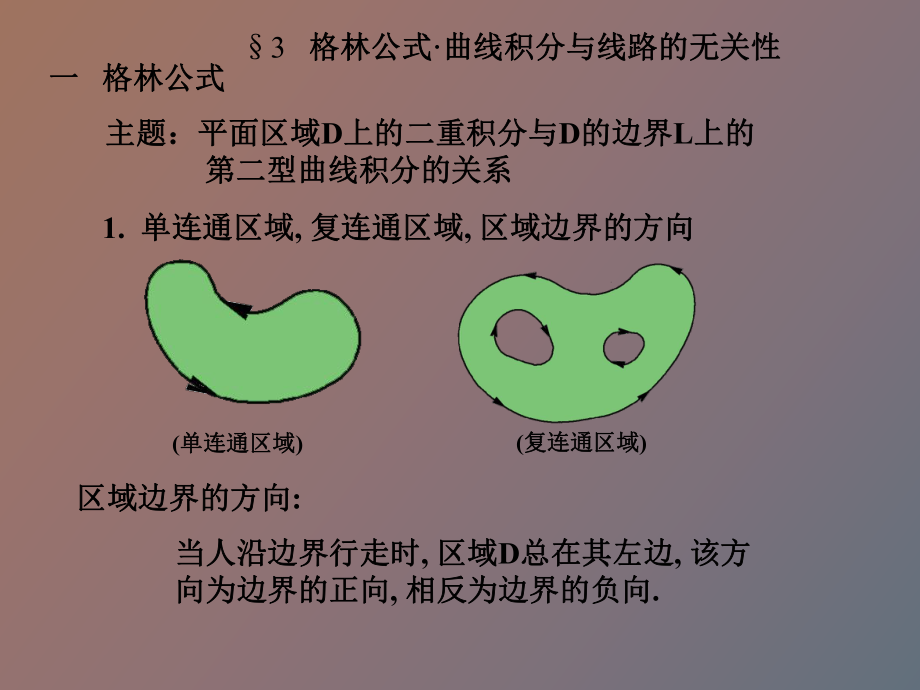
1、 3 格 林 公 式 曲 线 积 分 与 线 路 的 无 关 性一 格 林 公 式主 题 ： 平 面 区 域 D上 的 二 重 积 分 与 D的 边 界 L上 的 第 二 型 曲 线 积 分 的 关 系1. 单 连 通 区 域 , 复 连 通 区 域 , 区 域 边 界 的 方 向(单 连 通 区 域 ) (复 连 通 区 域 )区 域 边 界 的 方 向 :当 人 沿 边 界 行 走 时 , 区 域 D总 在 其 左 边 , 该 方向 为 边 界 的 正 向 , 相 反 为 边 界 的 负 向 . 2. 格 林 公 式定 理 22.3 若 函 数 P(x,y), Q(x,y) 平 面 有 界

2、 闭 区 域 D上 连 续 , 且 有 连 续 的 一 阶 偏 导 数 , 则( ) ( , ) ( , )LD Q P dxdy P x y dx Q x y dyx y 其 中 L为 D的 边 界 曲 线 , 并 取 正 向 . (1)公 式 (1)可 表 示 为 : ( , ) ( , ) LD x y dxdy P x y dx Q x y dyP Q (2)若 L为 复 连 通 区 域 ,则 L不 止 是 一 条 曲 线 . 2. 格 林 公 式( ) ( , ) ( , )LD Q P dxdy P x y dx Q x y dyx y 其 中 L为 D的 边 界 曲 线 , 并

3、取 正 向 . (1)证 : 只 要 证 ( , )LD P dxdy P x y dxy ( , ) LD Q dxdy Q x y dyx (i) 设 D为 x型 区 域 EC 1 2( , )| , ( ) ( )D x y a x b x y x 2( )( ) ( , )b xa x P x ydx dyy D P dxdyy ( , ( ) ( , ( )ba P x x P x x dx ( , ) ( , )AEB ACBP x y dx P x y dx ( , )ACBEAP x y dx 同 理 可 证 : ( , )LD Q dxdy Q x y dyx (ii) 若

4、D由 一 条 按 段 光 滑 的 闭 曲 线 围 成如 图 所 示 , 将 D分 为 D1, D2, D3由 (i)易 得 结 论 .(iii) 对 复 连 通 区 域 可 作 类 似 讨 论 . 定 理 22.3 若 函 数 P(x,y), Q(x,y) 平 面 有 界 闭 区 域 D上 连 续 , 且 有连 续 的 一 阶 偏 导 数 , 则( ) ( , ) ( , )LD Q P dxdy P x y dx Q x y dyx y 注 : 两 个 条 件 : P(x,y), Q(x,y) 及 它 们 的 偏 导 数 都 在 D连 续 ; D为 有 界 闭 区 域 ;(ii) 表 明 曲

5、 线 积 分 与 二 重 积 分 之 间 的 关 系 .(iii) 可 利 用 二 重 积 分 计 算 曲 线 积 分 , 可 利 用 曲 线 积 分 计 算 二 重 积 分 3. 例 例 1计 算 AB xdy 其 中 曲 线 AB是 半 径 为 r的 圆 在 第 一 象 限 部 分 .A Bo D解 : P(x,y)=0, Q(x,y)=x都 在 以 半 径 为 r的 四 分 之 一 圆 域 D连 续 .在 D上 用 格 林 公 式 , 得( , ) ( , ) ( )L D Q PP x y dx Q x y dy dxdyx y 其 中 L的 封 闭 曲 线 : AOBA 21( )

6、4D DQ P dxdy dxdy rx y ( , ) ( , )L Ao oB BAP x y dx Q x y dy xdy xdy xdy 0Ao xdy 0oB xdy 214BAxdy r所 以 214AB xdy r 例 2 计 算 2 2L xdy ydxx y 其 中 L为 任 一 不 包 含 原 点 的 闭 区 域 的 边 界 线 .DL解 : 因 为 2 2( , ) yP x y x y 2 2( , ) xQ x y x y 2 22 2 2( , ) ( )P x y y xy x y 2 22 2 2( , ) ( )Q x y y xx x y 显 然 , P(

7、x,y), Q(x,y) 及 其 偏 导 数 都 在 D连 续 , 由 格 林 公 式 , 得 2 2L xdy ydxx y ( ) 0D Q Px y 例 3 计 算 2 2L xdy ydxx y 其 中 L为 圆 心 在 原 点 半 径 为 r 的 圆 周 (取 正 向 ).解 : L的 参 数 方 程 为 cos ,0 2sin ,x r t ty r t 2 2L xdy ydxx y 2 2 0 cos cos sin ( sin )r t r t r t r t dtr 20 1 2dt 注 意 r 的 任 意 性 . 例 4 计 算 2 2L xdy ydxx y 其 中 L

8、为 以 原 点 内 点 的 有 界 闭 区 域 的 边 界 (取 正 向 ).L解 :任 作 圆 心 在 原 点 , 含 于 L内 的 圆 周 L1(设 其 半 径 为 r).L1设 L与 L1围 成 的 区 域 为 D, 则 由 例 2, 沿 D的边 界 的 正 向 的 第 二 型 曲 线 积 分 为 0, 即 12 2 2 2 0L Lxdy ydx xdy ydxx y x y 其 中 L取 逆 时 针 方 向 , L1取 顺 时 针 方 向 .12 2 2 2 2L Lxdy ydx xdy ydxx y x y (根 据 例 3) 4. 区 域 面 积 的 曲 线 积 分 形 式(

9、) ( , ) ( , )LD Q P dxdy P x y dx Q x y dyx y 若 P(x,y)= - y, Q(x,y)=x, 则 有2 ( )LD dxdy ydx xdy 故 D的 面 积 为 : 1 ( )2 L ydx xdy 例 5 求 由 星 形 线 3 3cos , sin ,(0 2x a t y b t t 所 围 成 的 面 积 .o x y解 :由 上 所 述 , 所 求 的 面 积 为1 ( )2 L ydx xdy 2 2 4 2 403 (sin cos cos sin )2ab t t t t dt 2 2 203 sin cos2ab t tdt

10、38ab 应 用 格 林 公 式 计 算 第 二 型 曲 线 积 分 :2 2 ,L xy dx x ydy(1) 其 中 L为 圆 周 2 2 2x y a 的 正 向 .2 2 2( ) ( ) ,L x y dx x y dy (2) 其 中 L是 以 A(1,1),B(3,2),C(2,5)为 顶 点 的 三 角 形 ,方 向 取 正 向 .sin ) ( cos ) ,x xAB e y my dx e y m dy (3) ( 其 中 m为 常 数 ,AB为 由 (a,0)到 (0,0)经 过 2 2 ( 0)x y ax a 上 半 部 的 路 线 . 二 曲 线 积 分 与 路

11、 线 的 无 关 性例 计 算 ,L xdy ydx 其 中 ：(i) 沿 抛 物 线 y=2x2, 从 O到 B的 一 段 ；(ii) 沿 直 线 y=2x 从 O到 B的 一 段 ；(iii) 沿 封 闭 线 路 OABO。 o xy (1,0)A (1,2)B解 :(i) L xdy ydx 1 20 (4 ) 2 x x x dx 1 206 2x dx (ii) L xdy ydx 10( 2 2 )x x dx 2(ii) L xdy ydx OAxdy ydx AB xdy ydx BO xdy ydx OA xdy ydx 10 0 0 0 x dx AB xdy ydx 20

12、1 0 2dy y BO xdy ydx OB xdy ydx 2 0L xdy ydx 定 理 22.4 设 D为 平 面 单 连 通 闭 区 域 . 若 函 数 P(x,y), Q(x,y)在 D内 连 续 , 且 有一 阶 连 续 偏 导 数 , 则 以 下 四 个 条 件 等 价 :(i) 沿 D中 任 一 按 段 光 滑 的 闭 曲 线 L, 有( , ) ( , ) 0. L P x y dx Q x y dy(ii) 沿 D中 任 一 按 段 光 滑 的 曲 线 L, ( , ) ( , ) . L P x y dx Q x y dy与 线 路 无 关 , 只 与 L的 起 点

13、终 点 有 关 ;(iii) ( , ) ( , )P x y dx Q x y dy是 D内 某 一 函 数 的 ( , )u x y 的 全 微 分 , 即 存 在D内 的 函 数 ( , ):u x y ( , ) ( , ) ( , ) . du x y P x y dx Q x y dy(iv) 在 D的 每 一 点 处 , 有 ( , ) ( , ). P x y Q x yy x 证 :(i) (ii)(i) 沿 D中 任 一 按 段 光 滑 的 闭 曲 线 L, 有( , ) ( , ) 0. L P x y dx Q x y dy(ii) 沿 D中 任 一 按 段 光 滑 的

14、 曲 线 L, ( , ) ( , ) .L P x y dx Q x y dy与 线 路 无 关 , 只 与 L的 起 点 终 点 有 关 ; ABR S设 ARB与 ASB为 联 结 点 A, B的 任 两 条 光 滑 曲 线 .由 (i) 0( , ) ( , ) L P x y dx Q x y dy 0( ) ( )ARB ASBPdx Qdy Pdx Qdy ARB ASBPdx Qdy Pdx Qdy 由 ARB与 ASB的 任 性 , 故 (ii)得 证 . 证 :(ii) (iii)(ii) 沿 D中 任 一 按 段 光 滑 的 曲 线 L, ( , ) ( , ) .L P

15、 x y dx Q x y dy与 线 路 无 关 , 只 与 L的 起 点 终 点 有 关 ;(iii) ( , ) ( , )P x y dx Q x y dy是 D内 某 一 函 数 的 ( , )u x y 的 全 微 分 , 即 存 在D内 的 函 数 ( , ):u x y ( , ) ( , ) ( , ) . du x y P x y dx Q x y dy由 (ii)知 ,曲 线 积 分( , ) ( , ) AB P x y dx Q x y dy与 积 分 路 线 无 关 , 故 当 B(x,y)在 D内 变 动 时 , 其 积 分值 为 B(x,y)的 函 数 .记 (

16、 , ) ( , ) ( , )ABu x y P x y dx Q x y dy 以 下 证 : ( , ) ( , ) ( , ) .du x y P x y dx Q x y dy 记 ( , ) ( , ) ( , ) . ABu x y P x y dx Q x y dy以 下 证 : ( , ) ( , ) ( , ) .du x y P x y dx Q x y dy ( , ), ( , )u uP x y Q x yx y 0 ( , ) ( , )lim ( , ),x u x x y u x y P x yx 0 ( , ) ( , )lim ( , ).y u x y

17、y u x y Q x yy ( , ) ( , )u x x y u x y ( , ) ( , ) ( , ) ( , )ABC ABP x y dx Q x y dy P x y dx Q x y dy( , ) ( , )BC P x y dx Q x y dy ( , )x xx P t y dt由 积 分 中 值 定 理 , 得 ( , )x x x P t y dt ( , )P x x y x 所 以 0 ( , ) ( , )limx u x x y u x yx 0lim ( , ) ( , ).x P x x y P x y 同 理 可 证 : 0 ( , ) ( , )

18、lim ( , )y u x y y u x y Q x yy (iii) (iv)(iii) ( , ) ( , )P x y dx Q x y dy是 D内 某 一 函 数 的 ( , )u x y 的 全 微 分 , 即 存 在D内 的 函 数 ( , ):u x y ( , ) ( , ) ( , ) . du x y P x y dx Q x y dy(iv) 在 D的 每 一 点 处 , 有 ( , ) ( , ). P x y Q x yy x由 (iii)有 ( , ) ( , ), xu x y P x y ( , ) ( , )yu x y Q x y又 P(x,y), Q

19、(x,y) 有 连 续 的 一 阶 偏 导 数 ， 故( , ) ( , )xy yu x y P x y( , ) ( , )yx xu x y Q x y ( , ) ( , ). P x y Q x yy x (iv) (i)(iv) 在 D的 每 一 点 处 , 有 ( , ) ( , ). P x y Q x yy x(i) 沿 D中 任 一 按 段 光 滑 的 闭 曲 线 L, 有( , ) ( , ) 0. L P x y dx Q x y dy设 L为 D中 任 一 按 段 光 滑 的 闭 曲 线 L, 记 L围 成 的 区 域 为 D1. 由 于 D为 单 连 通 区 域 ,

20、 故 D1含 在 D内 . 在 D1应 用 格 林 公 式 , 并 注 意 到( , ) ( , ), P x y Q x yy x得 1( , ) ( , ) ( ) 0. L D Q PP x y dx Q x y dy dxdyx y 定 理 22.4 设 D为 平 面 单 连 通 闭 区 域 . 若 函 数 P(x,y), Q(x,y)在 D内 连 续 , 且 有一 阶 连 续 偏 导 数 , 则 以 下 四 个 条 件 等 价 :(i) 沿 D中 任 一 按 段 光 滑 的 闭 曲 线 L, 有( , ) ( , ) 0. L P x y dx Q x y dy(ii) 沿 D中 任

21、 一 按 段 光 滑 的 曲 线 L, ( , ) ( , ) . L P x y dx Q x y dy与 线 路 无 关 , 只 与 L的 起 点 终 点 有 关 ;(iii) ( , ) ( , )P x y dx Q x y dy是 D内 某 一 函 数 的 ( , )u x y 的 全 微 分 , 即 存 在D内 的 函 数 ( , ):u x y ( , ) ( , ) ( , ) . du x y P x y dx Q x y dy(iv) 在 D的 每 一 点 处 , 有 ( , ) ( , ). P x y Q x yy x 注 : 1) D为 单 连 通 区 域 LL1 D

22、例 考 察 2 2L xdy ydxx y 其 中 L为 复 连 通 区 域 D的 边 界 (取 正 向 ).则 2 2( , ) yP x y x y 2 2( , ) xQ x y x y 2 2 2 2 2( , ) ( )P x y y xy x y 2 22 2 2( , ) ( )Q x y y xx x y 满 足 (iv): 在 D的 每 一 点 处 , 有 ( , ) ( , )P x y Q x yy x 满 足 (i)? 2) 通 常 用 (iv)来 判 断 第 二 型 曲 线 积 分 与 线 路 的 无 关 性 :( , ) ( , )P x y Q x yy x 例

23、判 断 下 列 积 分 是 否 与 积 分 线 路 有 关 :(1) ( )( )L x y dx dy (2) 2 , L ydx xdyx L为 右 半 平 面 的 路 线 .(3) 2 2 ,L xdx ydyx y L为 不 包 围 原 占 的 路 线 .(4) ( ) ,L x dx y dy (x),(y)为 连 续 函 数 . 3) 当 与 线 路 无 关 时 ， 从 A(x0,y0)到 B(x1,y1)的 第 二 型 曲 线 积 分 可 表 示 为1 10 0( , )( , ) ( , ) ( , )x yx y P x y dx Q x y dy4) 当 与 线 路 无 关

24、 时 ， 可 选 择 适 当 的 路 线 计 算 第 二 型 曲 线 积 分例 计 算 下 列 第 二 型 曲 线 积 分 :(1) (1,1)(0,0)( )( )x y dx dy (2) (1,2) 2(2,1) ,ydx xdyx L为 右 半 平 面 的 路 线 .(3) (6,8) 2 2(1,0) ,xdx ydyx y L为 不 包 围 原 占 的 路 线 .(4) (1,2)(2,1) ( ) ,x dx y dy (x),(y)为 连 续 函 数 . 5) 原 函 数若 ( , ) ( , ) ( , )du x y P x y dx Q x y dy 则 称 ( , )

25、( , ) ( , )u x y P x y dx Q x y dy为的 原 函 数 .当 ( , ) ( , )P x y Q x yy x 时 , ( , ) ( , )P x y dx Q x y dy 才 有 原 函 数 . 例 4 试 用 曲 线 积 分 求 (2 sin ) ( cos )x y dx x y dy 的 原 函 数 .解 : ( , ) 2 sin , ( , ) cosP x y x y Q x y x y 所 以( , ) cosP x y yy ( , ) cosQ x y yx 故 (2 sin ) ( cos )x y dx x y dy 有 原 函 数 , 且 0 0( , )( , )( , ) (2 sin ) ( cos )X YX Yu X Y x y dx x y dy 就 是 (2 sin ) ( cos )X Y dX X Y dY 的 一 个 原 函 数 .A BC取 (X0,Y0)=(0,0) , 并 按 如 图 路 线 计 算 u(X,Y), 得( , )(0,0)( , ) (2 sin ) ( cos )X Yu X Y x y dx x y dy 0 02 cos X Yxdx X ydy2 sinX X Y 故 所 求 的 原 函 数 为 : 2( , ) sinu x y x x y