量子力学——薛定谔方程

《量子力学——薛定谔方程》由会员分享，可在线阅读，更多相关《量子力学——薛定谔方程（50页珍藏版）》请在装配图网上搜索。

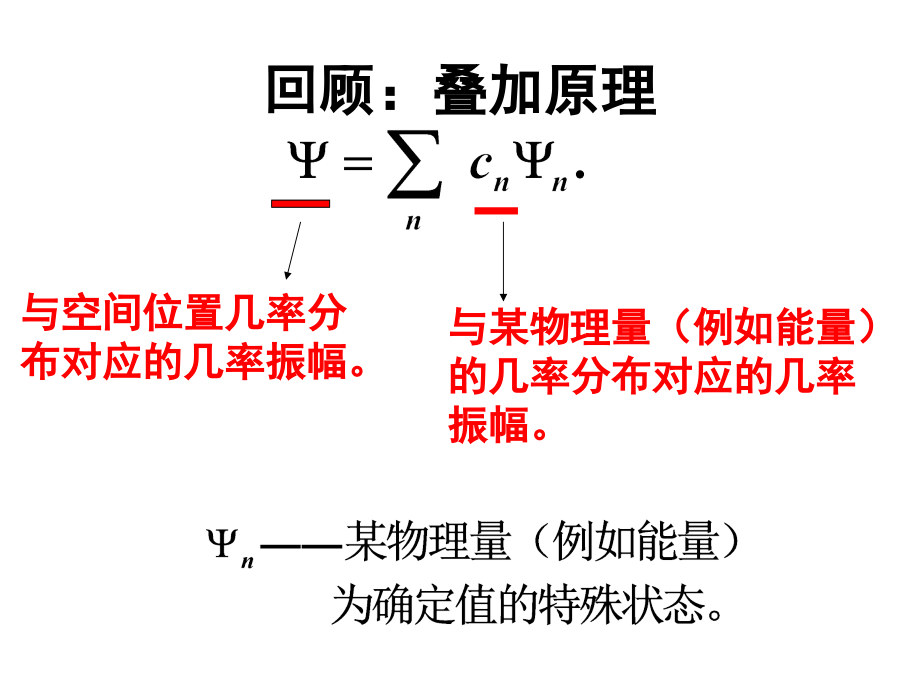
1、回顾：叠加原理回顾：叠加原理与某物理量（例如能量）与某物理量（例如能量）的几率分布对应的几率的几率分布对应的几率振幅。振幅。与空间位置几率分与空间位置几率分布对应的几率振幅。布对应的几率振幅。常数相位常数相位绝对绝对常数常数相位没有意义相位没有意义相对相对常数常数相位才是有意义的相位才是有意义的依赖于依赖于可观测。可观测。变化的相位是有意义的（能够在测变化的相位是有意义的（能够在测量中反映出来）量中反映出来）动量几率幅动量几率幅补充说明：波粒二像性的理解补充说明：波粒二像性的理解保留经典概保留经典概念的特征念的特征 不具有经典不具有经典概念的特征概念的特征 粒子性粒子性 有确定的质有确定的质量

2、、电荷、量、电荷、自旋等自旋等 没有确定的没有确定的轨道轨道 波动性波动性 有干涉、衍有干涉、衍射等现象射等现象振幅不直接振幅不直接可测可测 注意的问题注意的问题我们学习的课程的量子部分作了一个我们学习的课程的量子部分作了一个假设：粒子所处的状态可以由一个波假设：粒子所处的状态可以由一个波函数描述。函数描述。对更复杂的情况，状态不确定（不能对更复杂的情况，状态不确定（不能由一个波函数描述），需要借助于统由一个波函数描述），需要借助于统计方法（统计部分讲）。计方法（统计部分讲）。2.2 2.2 薛定谔方程薛定谔方程1.薛定谔方程薛定谔方程 量子力学的基本定律是波函数所满足量子力学的基本定律是波函

3、数所满足的偏微分方程。的偏微分方程。这个基本定律在本质这个基本定律在本质上是一个假说。上是一个假说。德布罗意物质波概念德布罗意物质波概念推广推广薛定谔方程的薛定谔方程的“建立建立”寻找寻找de Brogliede Broglie波满足的方波满足的方程，并加以推广程，并加以推广这不是严格推导（薛定谔方程不这不是严格推导（薛定谔方程不能由旧理论严格导出）能由旧理论严格导出）由由de Broglie波波 寻找寻找de Brogliede Broglie波满足的方程波满足的方程所以又因有有再推广到含有势能再推广到含有势能U的情况的情况两边作用于波函数记住便于记忆的形式t=0t=T量子力学量子力学 U

4、U（r r）经典力学：经典力学：力力 F F初始状态（依赖于实验制备）决定任意初始状态（依赖于实验制备）决定任意 T T 时时刻的状态，即刻的状态，即“态的演化过程态的演化过程”是确定的是确定的。x多粒子（N个粒子）情况非定域性：非定域性：整个体系的整个体系的状态状态用用3N个个空间坐标空间坐标和和一个时间坐一个时间坐标描述。标描述。2.2.几率守恒定律与几率流密度几率守恒定律与几率流密度由薛定谔方程导出一个反映几率守恒的定由薛定谔方程导出一个反映几率守恒的定律，从而引入律，从而引入几率流密度概念。几率流密度概念。几率密度几率密度根据薛定谔方程几率流密度的推导（单粒子）几率流密度的推导（单粒子

5、）几率密度的时间演化：几率密度的时间演化：薛定谔方程薛定谔方程定义流密度定义流密度记记则则这是薛定谔方程造成的结果，这是薛定谔方程造成的结果，代表一种代表一种守恒定律守恒定律。由于。由于w是几率密度，所以是几率密度，所以J可可以理解为几率流密度。以理解为几率流密度。理解（推导积分形式）理解（推导积分形式）对任何体积对任何体积V V，对上式积分，对上式积分等式右方用等式右方用GaussGauss定定理，得理，得VSV内部几率变化内部几率变化由边界流入或流出的量。由边界流入或流出的量。薛定谔方程能够满足全空间几率守恒薛定谔方程能够满足全空间几率守恒代表全空间几率守恒，实际上也就是粒子数守代表全空间

6、几率守恒，实际上也就是粒子数守恒。恒。薛定谔方程的这一性质是独特的。薛定谔方程的这一性质是独特的。相对论情况薛定谔方程不成立，以上结果也不相对论情况薛定谔方程不成立，以上结果也不成立（成立（有粒子产生和消灭，粒子数一般不守恒！有粒子产生和消灭，粒子数一般不守恒！）电流密度电流密度电流密度电流密度可以计算原子内部电子的电流可以计算原子内部电子的电流可以计算超导体等量子系统的电流。可以计算超导体等量子系统的电流。几率流密度表达式的另一种形式几率流密度表达式的另一种形式c.c.代表前面一项的复共轭。例题对平面波情况对平面波情况 求几率流密度求几率流密度3.3.薛定谔方程的求解薛定谔方程的求解定态薛定

7、定态薛定谔方程谔方程方程求解方程求解-分离变量法：分离变量法：设设代入薛定谔方程代入薛定谔方程先找特解（一系列基本先找特解（一系列基本函数），再叠加成通解。函数），再叠加成通解。两边同时除以两边同时除以左边（左边（t t）=右边（右边（r r）任意任意t t，r r均成立，而左边与均成立，而左边与r r无关，所以右边与无关，所以右边与r r也应该也应该无关无关；右边与右边与t t无关，所以左边也应该与无关，所以左边也应该与t t无关。所以两无关。所以两边都等于一个与边都等于一个与t t，r r都无关的常数都无关的常数E E时间部分时间部分空间部分（定态薛定谔方程）空间部分（定态薛定谔方程）定态

8、薛定谔方程定态薛定谔方程定态概念定态概念完整的定态波函数（定态薛定谔方程的解完整的定态波函数（定态薛定谔方程的解乘以时间因子）乘以时间因子）对比对比de Broglie波，我们发现常数波，我们发现常数E 的物理意义正是粒子的能量的物理意义正是粒子的能量。定态就是能量定态就是能量E确定的状态。确定的状态。定态下可观测量（如几率密度、几率流密度、定态下可观测量（如几率密度、几率流密度、动量几率密度等）都是动量几率密度等）都是稳定稳定的（不随的（不随t变化）变化）与玻尔原子模型中的定态概念类似，但是没与玻尔原子模型中的定态概念类似，但是没有有“轨道运动轨道运动”假设假设在可观测量中被约去在可观测量中

9、被约去定态薛定谔方程就是能量本征方程定态薛定谔方程就是能量本征方程含时薛定谔方程的一般解常数（由初始条件定出）常数（由初始条件定出）思考题思考题两个不同的定态叠加生成的态是否两个不同的定态叠加生成的态是否是定态？是定态？提提示示：4.4.波函数应满足的条件波函数应满足的条件从波函数的几率解释以及波函数满足二阶从波函数的几率解释以及波函数满足二阶微分方程这一要求，一般地说，波函数应微分方程这一要求，一般地说，波函数应该满足以下三个条件：该满足以下三个条件：(1)(1)单值性；单值性；(2)(2)有限性；有限性；(3)(3)连续性。连续性。连续性通常意味着连续性通常意味着 和和 都连续，都连续，但

10、在势能有无穷大跳跃的地方，但在势能有无穷大跳跃的地方，允许不连续。允许不连续。2.3 2.3 一维运动问题的一般分析一维运动问题的一般分析1.一维定态薛定谔方程的解的一般性质一维定态薛定谔方程的解的一般性质 二阶常微分方程，容易求解二阶常微分方程，容易求解它的解有如下的规律它的解有如下的规律WronskianWronskian定理定理若若 都是方程的解都是方程的解(能量相同能量相同)，则，则(c c 是与是与 x x 无关的常数无关的常数)，称为称为WronskianWronskian定理。定理。WronskianWronskian定理的证明定理的证明证明：定态方程的两个解满足证明：定态方程的

11、两个解满足另外两个定理另外两个定理共轭定理：若共轭定理：若 是定态行薛定谔程是定态行薛定谔程的解，则的解，则 也是该方程的解也是该方程的解(且且能量能量E E相同相同)。反射定理：对反射定理：对 (原点对称的原点对称的势势)，那么若，那么若 是该方程的解，则是该方程的解，则 也是该方程的解也是该方程的解(且能量且能量E E相同相同)。（由定态薛定谔方程可以直接证明，请自（由定态薛定谔方程可以直接证明，请自己完成）己完成）2.一维定态的分类一维定态的分类束缚态与非束缚态束缚态与非束缚态束缚态：束缚态：相反的情况是非束缚态（或称为散射态）相反的情况是非束缚态（或称为散射态）Ex条件条件：能量能量例

12、子例子束缚态：原子中的束缚态：原子中的“束缚束缚”电子电子 人工量子微结构人工量子微结构束缚态几率分布被限制在有限的空间范围内。束缚态几率分布被限制在有限的空间范围内。非束缚态：如自由电子；从原子中电离出去非束缚态：如自由电子；从原子中电离出去的电子的电子3.3.一维束缚态的一般性质一维束缚态的一般性质先引入一个概念简并与非简并先引入一个概念简并与非简并如果对一个给定的能量，只有一个线性独立的波如果对一个给定的能量，只有一个线性独立的波函数存在（函数存在（即只有一个状态即只有一个状态），则称该能级），则称该能级是非是非简并简并的，否则称它是简并的，其的，否则称它是简并的，其线性独立的线性独立的

13、波函波函数的个数称为它的简并度数的个数称为它的简并度。线性独立的定义：对常数线性独立的定义：对常数c1，c2一维束缚态不简并定理一维束缚态不简并定理定理：一维束缚态必是非简并态（定理：一维束缚态必是非简并态（可以由Wronskian定理证明）。）。En不简并定理不简并定理的证明的证明证明（证明（反证法反证法）：）：假设简并假设简并，则方程有两个线，则方程有两个线性独立的解，但是由性独立的解，但是由 WronskianWronskian定理定理：两个函数不是线性独立的（对应同一个状态），两个函数不是线性独立的（对应同一个状态），因此因此不简并不简并。与题设矛盾，故定理得证。与题设矛盾，故定理得证

14、。*更严格的证明应该考虑波函数有节点（为零的点）的情况，这时更严格的证明应该考虑波函数有节点（为零的点）的情况，这时需要分段考虑每个节点之间的区域，再利用波函数连续性条件证需要分段考虑每个节点之间的区域，再利用波函数连续性条件证明以上常数明以上常数C对每一段是同一个常数（可参考曾谨言量子力学卷对每一段是同一个常数（可参考曾谨言量子力学卷1，83页）页）对定理的补充说明对定理的补充说明（1 1）此定理仅对一维情况成立此定理仅对一维情况成立；二维、三维；二维、三维束缚态的能量仍然可能简并（如氢原子、束缚态的能量仍然可能简并（如氢原子、二维、三维谐振子等）；二维、三维谐振子等）；（2 2）非束缚态的

15、能量一般是简并的。）非束缚态的能量一般是简并的。两个推论两个推论推论推论1 1：一维束缚态波函数的相位必是常数。：一维束缚态波函数的相位必是常数。即即 因此波函数可以取为实函数因此波函数可以取为实函数推论推论2(2(宇称定理宇称定理)：如果：如果 则一维束缚态波函数必有确定的宇称则一维束缚态波函数必有确定的宇称（奇（奇偶性）。偶性）。宇称的定义宇称的定义作业作业作业作业(补充题补充题2.2)2.2)：证明本节中的：证明本节中的推论推论1 1和和推论推论2 2。p.52,#2.2p.52,#2.2，注意：在球坐标中，注意：在球坐标中,提示下次课内容2.4 2.4 一维无限深势阱、有限深势阱一维无限深势阱、有限深势阱 2.5 2.5 线性谐振子线性谐振子