西北大学_茹少锋管理运筹课后答案

《西北大学_茹少锋管理运筹课后答案》由会员分享，可在线阅读，更多相关《西北大学_茹少锋管理运筹课后答案（95页珍藏版）》请在装配图网上搜索。

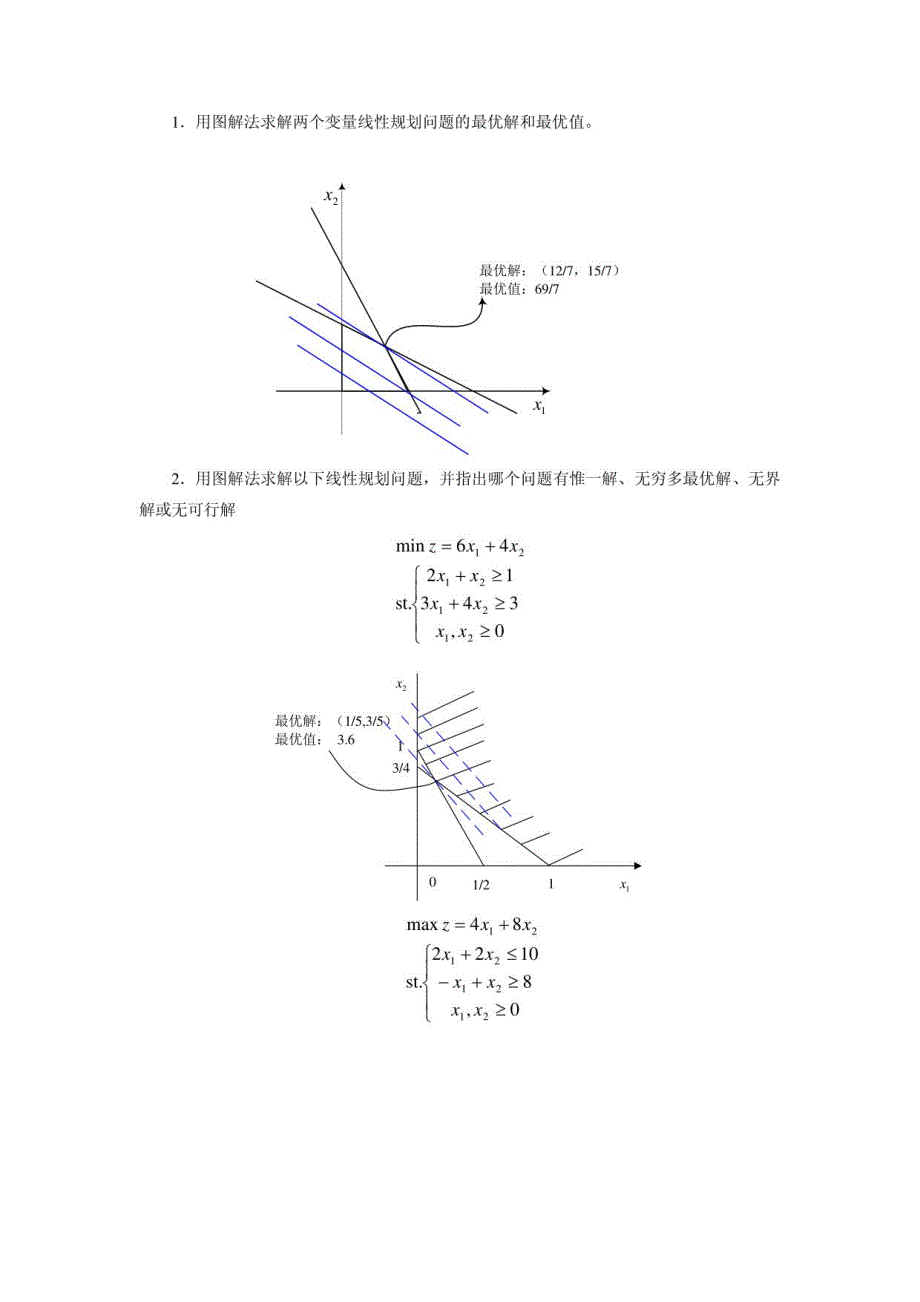
1、1.用图解法求解两个变量线性规划问题的最优解和最优值。2.用图解法求解以下线性规划问题，并指出哪个问题有惟一解、无穷多最优解、无界解或无可行解min z=6项+4x22x+x2 1st.3x x2 0最优解:最优值:max z=4工1+8x22x1+2X2 0无可行解3.某公司从中心制造地点向分别位于城区北、东、南、西方向的分配点运送材料。该公司有2 6 辆卡车，用于从制造地点向分配点运送材料。其中有9 辆，每辆能装5吨的大型卡车，1 2 辆每辆能装2吨的中型卡车和5辆每辆能装1 吨的小型卡车。北、东、南、西四个点分别需要材料1 4 吨、1 0 吨、2 0 吨、8 吨。每辆卡车向各分配点送材料

2、一次的费用如表2-7 所示。建立运送材料总费用最小的线性规划模型。表2-7 车辆运送一次的费用北东南西大80639275中50605542小20153822解 设大、中、小型车分别用i 表示，则 =1，2,3；东、南、西、北四个分点分别用/表示，则 1 =1 2 3,4；向/方向发出的，型车数量为冏。mi n Z =80XH 4-63XI2+9 2 1 3+75X14+50X21+6 0 x2 2+5 5 x2 3+4 2 x2 4+20X31+15X32+38x33+22X34st.0,z,j=l,2,3,44.某工厂生产A、B、C 三种产品，现根据合同及生产状况制定5 月份的生产计划。已知

3、合同甲为：A 产 品 1000件，每件价格为500元，违约金为100元/每件；合同乙：B 产品 500件，每件价格为400元，违约金为120元/每件；合同丙为：B 产品600件，每件价格为420元，违约金为130元/每件；C 产品600件，价格400元/每件，违约金为90元/每件。有关各产品生产过程所需工时以及原材料的情况如表2-8所示。试以利润为目标建立该工厂生产计划的线性规划模型。表2-8产品使用的原材料、加工工序、资源限制、成本产品A产品B产品C资源限制工时或原材料成本工 序1212460015工序2311400010工序3232600010原 料13241000020原料2432800

4、040其他成本101010解 设 工 厂 5 月份为完成合同甲生产七件A 产品；为完成合同乙生产七件B 产品；为完成合同丙生产七 件 B 产品，龙4件 C 产品.maxZ=500 x,-(1000-x,)+400 x2-(500-x2)x120+420 x3-(600-x3)X130+400X4-(600-X4)X90-(2X15+3X10+2X10+3X20+4X40+10)X1-(15+10+3x10+20 x2+3x 40+10)x(x2+x3)-(2x15+10+2x20+4x20+2x40+10)与=2902+295X2+325X3+260%-292000st，2xt+x2+x3+2

5、X4 4 6 0 03 x1+x2+x3+2X4 4 0 0 02七+3X2+3X3+2X4 6 0 0 03 X 1 +2(X2+)+4X4 1 0 0 0 04 X 1 +3(X2+X3)+2X4 8 0 0 00 1 0 0 0,0 x2 5 0 0,0 x3 6 0 0,0 x4 6 0 0,5.某公司从事某种商品的经营，现欲制定本年度1 0至1 2月的进货及销售计划。已知该种商品的初始库存量为2 0 0 0件，公司仓库最多可存放1 0 0 0 0件，公司拥有的经营资金8 0万元，据预测，1 0至1 2月的进货及销售价格如表2-9所示。若每个月仅在1号进货1次，且要求年底时商品存量达到

6、3 0 0 0件，在以上条件下，建立该问题的线性规划模型，使公司获得最大利润？（注：不考虑库存费用）表2-9进货和销售价格月份101112进货价格/（元/件）909598销售价格/（元/件）100100115解 七/=1 0,1 1,1 2,为每月购进的货物，X，i =I。1 J2为每月销售的货物。ma x Z =1 0 0)%+1 0 0 yu+1 1 5%9 0 xl 0-9 5 x -9 8 xl 29 0 x1 0+9 5 x +9 8/8 0 0 0 0 资金限制2 0 0 0+x1 0 1 0 0 0 0 库容限制X”+2 0 0 0 +xl 0-yl 0 1 0 0 0 0 库容

7、F艮制xp+x”+2 0 0 0 +xl 0 X o y”4 1 0 0 0 0 库容F艮制yl 0 2 0 0 0 +xl 0 销量限制 xl t+2 0 0 0 +xl0-y1 0 销量限制y1 2 0,j =1 0,1 1,1 2X 0,/=1 0,1 1,1 26.某饲养场饲养动物出售，设每头动物每天至少需7 0 0 g蛋白质、30 g矿物质、1 0 0 m g维生素。现有五种饲料可供选用，各种饲料每公斤营养成分含量单价如表2-1 0所示。表2-1 0饲料所含的营养成分及价格饲料蛋白质/g矿物质/g维生素/g价格/（元依 T）1310.50.2求这个问题的规划模型，使既满足动物生长的需

8、要，又使费用最小的选用饲料的方案。220.51.00.7310.20.20.446220.35180.50.80.8解 设 各 送 这 5 钟饲料玉，X2,x3,X4,X5 kgom inZ =0.2 x)+0.7 x2+0.4x3+0.3x4+0.8 x5StA3匹 +2X2+/+6匕+1 8尤5-7 0 0/+0.5X2+0.2/+2X4+0.5X5 300 5%+x2+0.2/+2X4+0.8%-I。xt,i=1,2,3,4,57.某一企业家需要找人清理5间会议室、1 2 张桌子和1 8 个货架。今有两个临时工A和 B可供该企业家雇佣。A 一天可清理1 间会议室、3 张桌子与3 个货架；

9、而 B 一天可清理 1 间会议室、2 张桌子与6 个货架。A的工资每天2 5 元，B每天2 2 元。为了使成本最低,应雇佣A和 B各多少天？（用线性规划图解法求解）解：设雇佣A和 B分别为乂p 天m inZ =2 5 x +2 2 yst.53x+2 y 123x +6 y 1 8N O且 为 整 数由图知A点为最优解，联立方程：3x+2y=12=25x2+22x3=116因此，雇佣A工人2天，B工 人3天。8.某外贸公司专门经营某种杂粮的批发业务。公司现有库容5000担的仓库。1月1日,公T拥有库存1000担杂粮，并有资金20000元。估计第季度杂粮价格如表2-11所示。表2-1 1第一季度

10、杂粮价格表进货价/元出货价/元1月2.853.102月3.053.253月2.902.95如果买进的杂粮当月到货，但需到下月才能卖出，且规定“货到付款公司希望本季度末库存为2000担，建立该问题的线性规划模型使三个月总的获利最大。解设一月份买入为担，卖出工；担；二月份买入 担，卖出巧 担；三月份买入刍担，卖出均担。maxZ=3.10 x；2.85+3.25x2-3.05x2+2.95x3-2.90 x32.853 200001000-x；+X 50003.05x2 20000-2.85%,+3.10 x；st.1000-X j+X +x,K 50002.90X3 0,z=1,2,3;X/0,J

11、=1,2,31.求下列线性规划问题的所有基解、基可行解、最优解max z=3/+%+3x3解:由题意知：A=V(1)B=(0。),项+=2s t.0I R、2 4J=(P 1,P 2.P 3)b=l6J c=(3,1,3)Bd邦，B 1是基，石，是基变量，/是非基变量，令七=0,得玉=一2,x2=4即lx3L(-2,4,0)T为基解，但不是基本可行解。(2)B2=(/”3),|如 邦,鸟 是基,王，七是基变量，是非基变量。令%2=0,得 =2/3,x3=3/4,即 I X 3I304为基解，同时为基本可行解,Zmax=(2/3)*3+0+4/3*3=6。(3)&=(P 2,P 3),|鸟I和，

12、鸟是基,%2,七是基变量，苍是非基变量，令年、了2再=0 ,得%2=1 ,X3=1 ,即(工3 仅、1=J为 基 解，同时为基本可行解,Z m a x=1+3=4。综上所述,）卜2、4X2基解为131其中第二个和第三个为基本可行解，为最优解。2.分别用图解法和单纯形法求解下列线形规划问题，并指出单纯形法迭代的每一步相当于图形上哪一个顶点max z=211+3x2St/X j-x2 1jj 0书,图解法知线性规划模型的可行域如阴影部分所示,令z=0，1，2.时，m a x z逐渐增大，可行域是无界的，所以，此模型是无界解。（2）单纯形法:化为标准型为:max z=2工 +3x2+Ox3+0 x4

13、st.0(-1 1 0、A=L 0 0 bXB2玉30 130%对应图中原点。以 1 为轴心项，换基迭代，得01-11010410012a2300此时对应图中A点，坐 标 是（1,0）以 1 为轴心项，换基迭代，得CBXH2 玉3 x?00%b21-1101001-111o 05-20-2CBXB2 斗3 X20 1 30%b2不100123X?01-111a0035-7此时对应图中B点，坐 标 是（2,3）因 为，b 3=5 0,同时W对应的列小于等于0,则原模型有无界解。maxz=2%j+5x2x,42光 2 12st.3/+2X2 0解（1 ）图解法:坐标为(2,6),m a x z=3

14、4(2)单纯形法：化为标准型为：m a x z =2%+5 x2+O x3+0 x4+O x5X)4-x3=42x0+xA=1 2St.0J=192 5单纯性表如下:q0100、r4、A 二020101 2、32001=(P 1.P 2，P 3，P 4，P 5 )b=、8 ,C=(2,5,0,0,0)W B=(P 3，P 4，P 5)为 可 行 基,CB=(0,0,0)此时对应图中。点，坐 标 为（0,0）,以 1 为轴心项，换基迭代，得CBXB2 xi5*20 0 X4015b0当1 010040%020101 20X5320011 8(T25000CBXB2%5%20 1 30%0X5b2

15、玉1010040%02010120X502-3016o05-200-8此时对应图中A点，坐 标 为（4,0）以2为轴心项，换基迭代，得CB无62%5X20天0%0 x5b21010040003 1-16501-3/201/23CT0011/20-2/5-23此时对应图中B点，坐 标 为（4,3）以3为轴心项，换基迭代，得CBXB2%5*20 X30%0X5b2X100-1/31/320X30011/3-1/325X20101/206a000-11/6-2/3-34由于 基=0,。非 基 0,所以存在唯一解，也是最优解。此 时 对 应 图 中 C 点，坐标为(2,6),max z=2*2+5*6

16、=34,(X1,x2,x3,x4,x5 Y=(2,6,2,0,0)7max z=2内 +4 x22X+2X2 12x,+2X2 8StJ3x2 0解：（i）图解法:可 行 域 如 图 阴 影 部 分，当z=0,1,2做 等 值 线，已 知2=2芯+4 与 直 线西+2%=8的斜率相同，当z与这条直线重合时，该模型取最大值，因此该模型有无穷多个 解，无 穷 多 个 解 是B,C两点线段中的点，m a xz=1 6此 时 对 应 图 中 点0,坐 标 为（0,0）,以2为轴心项，换基迭代，得(2)max?2st.*T/A=kC=(2单纯无单纯形法：化为标准型：=2x,+4X2+0 x3+0 x4+

17、0 x5r,+2X2+x3=1 2q +2X2+x4=93X2+x5=92 0 =1,2 52 2 1 0 0、12 0 100 3 0 0 1,4,0,0,0)B=(P 3，“4，P 5 )漆 为：，1 28=(PLP2，P3，P4，P5)b=(9CB=(0,0,0)X7CBXB2%4 1 20 xi0%0X5b022100120Z1201080X5030019(724000CBXB2%4X20 X 30 X 40%5b2111/2006001-1/21020X5030019b02-100-1 2此时对应图中点A,坐 标 为(6,0)以1为轴心项，换基迭代，得CBXB2%4X20 1 30%

18、0%5b2X101-1044X201-1/21020X5002/3-313c r000-20-1 6此时对应图中点B,坐 标 为(4,2)由于b4,又吃为非基变量，且/=0,且此列存在 正 数，则 此 线 性 规 划 模 型 有 无 穷 解。其 中 一 个 基 本 最 优 解 为(X|x2 x3 x4 X 5 )7 =(4 2,0,0,3)7 ,m a x z=2*4+4*2=1 63.用单纯形法求解下列线性规划问题m i n /=%)+2X2-x32xl 4-x2-x3 4x,-2X2+2X3 8s t x%1 +x2+x3 0解：化为标准型：m a x z =F -2X2+/+0 x4+O

19、 x5+0 x62%j+%+4=4%1 -2 M +2X3+/=8s t.0,7 =1,2.62 1 -11 -2 2.J 1 0令 B=(P 4，P 5，/单纯形表如下：1 0 0)(4、0 1 0 80 0 U b=H,6)B为可行基，CB二C=(0,0,-1,-2,10),0,0,0)CBXB.西212x30%0X50A6b0%21-110040X51-201080%1110015c r-1-2000以2为轴心项,换基迭代，得 基=0,0非 基 0,存在唯一-解，此时玉=0,彳3=4。m i n f=0+2*0-4=-4CBXB-x-2X2X30 X40X50%b0X45/20011/2

20、081X31/2-1101/2040X61/2200-1/211a-2/3-100-1/20-44.用大M法求解下列线性规划问题m a x/=5为 +9+3/$+4 1 2+21 3 之 1。s t J xx-2%2+与 4 1 6xpx2,x3 0解：化为标准型(加上人工变量a)：m a x/=5玉 +%+3X3+0 x4+0 x5-M a$+4X2+2X3-%+q =1 0s t J 再-2X2+&=1 6为2 0 =1,25以 2 为轴心项，换基迭代，得(4 2-1 04=U-2 1 0 1 0,10、b=V6J C=(5,1,3,0,0)XB5 司X23X30%0%-Mab-Ma142

21、-1011001-2101016(75+M1+4M3+2M-M00以 1为轴心项，换基迭代，得CB3 七0%0X5-Mab5玉142-101100不0-6-111-16(y0-19-750-5-M-10(M+5)由于第二列对应的检验数为110,并且所对应的列全小于0,则此线性规划模型的解是无界解。尤85 再3X 30 z0X 5-Mab5王1-2I010160%0-6-111-16(T011-20-5-M-10(M+8)5.已知线性规划问题，用单纯形法计算时得到的中间某两步的计算表见表3-16所示,试将表中空白处的数字填上。表 3-1 6 单纯形迭代中的两步计算表cBXB3%5X24巧0 x4

22、0%0%bX22J10130083X5305_2110143%5304_2301203CZ j304_ 35 006.已知线性规划问题m a x z=C X +，22+C 3X 35X20101541841_ J 04180414X3001_ 6 _4154144150413X 100_ 2_41_ J 24115414441CJ一 Z j452411556010414141123st/ciX+a1 2x2+|3X3+X4-b%无+22X2+%与 +%5 =%X/0,j=l,-5用单纯形法求解，得到最优单纯形表如表如表3-1 7所示:表3-1 7最终单纯形表XBxx2X3X4X5bX31011

23、2_ 123.2x21210-122crzi-3000-4求“1 1，0 1 2，4 1 3,4 21，“22，23，1，”2 的值;求C|，C2，C 3的值。解：由题意可知：初始的基变量是工4,%,将最终单纯形表的基变量通过迭代转换为4,X5,还原成最初单纯形表，如下:XBX2X 3X4X 5b与9214108%5212015从而得出:A9所以，即=24=80crzj923600141 225J“1 2=1b2=5,12017b=(5.C=I，3,6,0,0%3 =45a2=2a22=1 a23=292 c2=3 c3=67.某公司生产1、2两种产品，市场对1、2两种产品的需求量为：产 品1

24、在1-4月每月需求10000件，5-9月每月30000件，10-12月每月100000件，产品2在3-9月每月需求15000件，其它月每月50000件，该公司生产这两种产品的成本为：产 品1在1-5月内生产每件5元，6-12月内生产每件4.5元；产 品2在1-5月内生产每件8元，6-12月内生产每件7元。该公司每月生产这两种产品的能力总合不超过120000件 产 品1容积每件0.2立方米,产品2每件0.4立方米，该公司仓库容量为15000立方米，占用公司仓库每月每立方米库容需1元：如该公司仓库不足时，可从外边租借，租用外面仓库每月每立方米库容需1.5元。试问在满足市场需求的情况下，该厂应如何安

25、排生产，使总的费用最小？8.某炼油厂使用三种原料油甲、乙、丙混合加工成A、B、C三类不同的汽油产品，有关数据如下表3-18所示。另外，由于市场原因，A的产量不得低于产品总量的40%。问该厂应如何安排生产才能使其总利润最大？表3-18三种原料的信息产.产规品原ABC原料成本（千元/吨）原料限量（吨）甲6 0%21 5%1.8 0 020 0 0乙1.3 5 025 0 0丙20%6 0%5 0%0.9 0 01 20 0加工费（千元/吨）0.4 5 00.3 6 00.27 0售 价（千元/吨）3.0 6 02.5 6 52.0 25解：设/，X 2,2分别为A产品中甲、乙、丙的成分；X 4,“

26、5,七分别为B产品中甲、乙、丙的成分；X i,4，不分别为C产品中甲、乙、丙的成分。由题意，有m a x z=(3.0 6 0-0.4 5 0)*(xl+x2+x3 )+(2.5 6 5-0.3 6 0)*(4 +x5 +x6)+(2.0 25-0.27 0)*(x7 +x8 +x9)-1.8 0 0*(/+乙+*7 )-1.3 5 0*(2+x5 +x8 )-0.9 0 0*(尤3 +/+为)用计算机求解为:9.线性规划的目标函数是求其值的极大化，在标准的单纯形法求解过程中得到如下表（其中“1，”2是常数）表3-1 9求解中某一步的单纯形表CBXB2.q5X28 X 30 x40 x50X6

27、b0%030205x2H,12也0 x4-2-118-2%(1)在所有的空格上填上适当的数(可包含参数 2)(2)判断下面四种情况在什么时候成立，说明理由。1)此解为最优解，写出相应的基解和目标函数值；2)此解为最优解，且此线性规划有无穷多最优解；3)此规划有无界解；4)此解不是最优解，但可用单纯形法得到下一个基可行解。解 2(2)1)当2-5 i 0且&0且“1 0且”20,即0 c H i 0时，此解不是最优解。1 0.表3-20是求某极大化线性规划问题计算得到的单纯形表。表中无人工变量，、。2、%、d、G、。2为待定常数。试说明这些常数分别取何值时，以下结论成立。表3-2 0极大化线性规

28、划问题计算得到的单纯形表XBX|x2X3X4X5尤6bX34a10a20dX4-1-301-102X6%-500-413c-7 r r 0 0-30cj zj c C1表中解为惟一最优解；表中解为最优解，但存在无穷多最优解；该线性规划问题具有无界解；表中解非最优，为对解改进，换入变量为，换出变量为分解（1）当 归0,Cl 0 且c2 0,此线性规划模型有唯一解。（2）当听0,G=0 或 02=0,%0 且 0,ci 0且 4 1 2,表中解非最优，为对解改进，换入变量为，换出变量为与。第四节1.写出线性规划问题的对偶问题。m a x z=10%,+3x2+5 x32内 +5X2+x3 15s

29、t.4X +3匕 0m a x z=5 尤+6x2+3x3xl+2X2+2X3=5X 1+5 与 一刍 2 3s t/+7X2+3 九3 0,x3 6X2+4 3 +x5 0,x4 lMz 0 (j=1,2,;i=1,2,m)解：（1）m in 6 9=15 y i+7 y 22y1+4y2 10s t/5 y,3%+3 y2 5%,为 N O(2)m in co=5 y+3y 2 +8%y,-y2+4 y3=52 y +5%+7”2 6s t.2%-%+3%4 3,无 约 束，为 0（3）m a x co=6 y l+8 y 2 +0乂s tx3%+2y 3 W 35月 +2-3y 3 32

30、2y1 0,y2 0,乃无约束m nm a x=2。汹+2%jj=i j=im ny v；+y u.c：-ss”L 乙 A)Ji(=1 ；=i片,无 约 束(i =1,2.m;j=1,2,.,n)2.判断下列说法是否正确，并说明理由。(1)如果线性规划的原问题存在可行解，则其对偶问题也一定存在可行解(2)如果线性规划的对偶问题无可行解，则其原问题也一定无可行解(3)在互为对偶问题的一对原问题与对偶问题中，不管原问题是求最大或最小，原问题可行解的目标函数值一定不超过其对偶问题的可行解的目标函数值(4)任何线性规划问题具有唯一的对偶问题解：(1)不正确。因为当原模型存在可行解且目标函数值无界时.，

31、其对偶模型无可行解。(2)不正确。因为对偶模型无可行解，其原模型可能存在可行解且目标函数值无界。(3)不正确。当原模型求最小值时，原模型的F I标函数值可能超过对偶模型的目标函数值。(4)正确。对偶模型具有对称性。3.用计算机求解线性规划问题，说明每一种资源的影子价格。m a xz=5()X +100X +尤2 4 3002X(+x2 400 x2 0解：计算机求解结果如卜图所示:sHJ Linear PrograBaing R esults4.3 SolutionX1X2RHSDualMaximize50.100.Constraint 11.1.=300.50.Conshaint 22.1.

32、=400.0.Constraint 30.1.=250.50.Solution-)50.250.$27.500.由图可知，原模型的最优解为(5 0,25 0),其对偶模型的最优解为(5 0,0,5 0),三个约束条件的影子价格分别为5 0,0,50。4.某企业生产甲、乙两种产品，其单位利润分别为2 元 和 3 元。每生产一件甲产品需劳动力3 个，原材料2 个单位。每生产一件乙产品需劳动力6 个，原材料1个单位。企业现有劳动力24个，原材料10单位。试问：(1)该企、也应如何安排生产才能获得最大利润？(2)若另一个企业想利用该企业的这两种资源(劳动力和原材料)，该企业最低应以多少价格转让？解：设

33、该企业生产甲产品占个，乙产品 个，禾！润 为 z,建立模型为max z=2/+3x2st.3七 +6X2 242x1+0(1)化为标准型max z=lOXj+3x2+0 x3+0 x4st.0A，25311、c=(1 0,3,0,0),b=(2 40 0丫,最初唯纯形表X。2 玉3X20X4b2 5102 4X22 1001 0(T 2 3经过换基迭代后，形成最优单纯形表00Xb2xi3 X 20X305bx2012/9-1/32X110-1/91/34a00-4/9-1/3由最优单纯形表可知，最优解为(4,2,0,0),即应生产4个甲产品，2个乙产品，获利最大。(2)由(1)中最优单纯形表知

34、对偶模型最优解为(4/9,1/3),因此，最低转让价应为2 4*4/9+1 0*1/3=1 4(元)。5.已知线性规划问题m i n z=8占 +6x2+3 x3+6 x4X 6s t/+x4 2x,+x3 2与 NO,/=1,2,3,4(1)写出该问题的对偶问题(2)已知原问题的最优解为：X*=(1 1 2 0尸。根据对偶理论，直接求出对偶问题的最优解。解(1)对偶模型为m a x co=-3 yl +6 y2+2 y3+2 y4S t/_ yi +%+%8-2+y2 6%+%+丫4 W 3-M+%+丫3 6%0(2)根据对偶模型的互补松弛性理论，可知原模型的松弛变量与=0,%=0,/=0,

35、网=一1。设对偶模型最优解为了*，由互补松弛性可知，*4=0,所以工=0。又设对偶模型剩余变量为内,打，%,%,且均为正数，互补性有匕x*=0,于是得 当=儿=%=%=0,此时对偶模型的约束条件为-y：+y；+y；=8-2y；+y；=6*c为+%+N=3*/-X+为+%=6y：=。解之得)1=2 ,2 =1 0 ,3=-2 ,)4=0 O6.对线性规划问题m ax z=X +2X2+x3+x2-x3 2x,0,x2 W O,.无约束(1)写出其对偶问题；(2)利用对偶问题性质证明原问题目标函数值Z 4 1。解(1)对偶模型为m i n co=2yi+2 +2y3s t.1M -%+为 2-M

36、+h +%=1Ji 20,为无约束，丫3 4(2)取对偶模型的可行解(0,1,0),求得对偶模型的目标函数值为1,根据弱对偶性中原模型可行解目标函数值不可能超过对偶模型可行解目标函数值，可证得原模型目标函数值z4 1。7.给出线性规划问题m ax z=I 1+s t.+与 0,x2 0,x3 0利用对偶问题性质证明上述问题目标函数值无界。m i n 6 9 =2y+y2-乃-2 y2,力+为 2 1必 一 乃 N O解：对偶模型为：1力，乃？由图解法可知该线型规划模型无可行解，对于原模型可取七=2 =1 ,说明原模型有可行解，根据弱对偶性可知原模型目标函数无界。8.用对偶单纯形方法求解下列线性

37、规划问题m i n z=4 玉 +1 2 x2+1 8/m i n z=5玉 +2x2+4 鼻(1)s t.X +3X3 32X2+2X3 5x1,x2,x3 0(2)s t J+X2+2X3 46 X|+3X2+5X3 1 0X),x2,x3 0俯()化为标准型m ax z,=-4 xt-I 2x2-1 8 x3+0 x4+0 x5st/七一3 马+Z=32%2 -2%3+鼻=5X p X2,X3,X4,X5 0A=-1-2,c=(-4,-1 2,-1 8,0,0),b=(-3-57110用时偶单纯形法得初始单纯形表为Xb-4 x-1 2 X2-1 8x30X40*5b芍-10-310-3x

38、20-2-201-5a-4-1 2-1 800由(-4,-1 2,-1 8,0,0)4 0 可 知 B 为正则基；以2 金 为轴心项，换基迭代得X,-4xi-12 x2-18 13 0X4 0 x5X 4-10-3 10-3x20 110-1/25/2a-4 0-60-6以-3 8为轴心项，换基迭代得由于所有检验数b 2 0,Xb-4 x-1 2 X2-1 8x30X40X5bX31/30-1/3-1/301x2-1/311/31/3-1/23/2(7-20-2-2-6得到最优解为（0,3/2,1)（2）化为标准型maxz-5网-2x2-4x3+0 x4+0 x5-3xj%2 +z =4st.

39、-6X 一 3%2-5xj+Xj 10%1，%2,%3,%4,%5 0-3-2101A=6,c=(-5,-2,-4,0,0),b=(-4初始单纯彩表为Xb.5-4X30X40 x5bX4-3 e-1-210-4X5-6-3-501-1 0a-5-2-400以-3 为轴心项，换基迭代得Xb-5 x1-2X21/3-4x32/30X4-1/301 50b4/3X50-1 0-1-21-2a 0 -1/3以-产为轴心项，换基迭代得-2/3-5/30Xb-5/-2X20X40X5bx101/3-11/32/3x20112-12a 0由于所有检验数b2 0,0得到最优解为（-1/32/3,2,-10 ）

40、。-1/39.对下列线性规划问题min z=60当+40 x2+80.%s t x3x,+2X2+x3 24工1+/+3X3 42xl+2X2+2X3 3x,x2,x3 0（1）写出对偶问题；（2）用对偶单纯形法求解原问题；（3）用单纯形法求解其对偶问题；（4）比 较（2）与（3）中每一步计算得到的结果解（1）对偶模型max co=2yl+4 y 2+3y33丫1+4为+2%4 6 st 0（2）原模型化为标准模型得m ax/=-60 xj-40 x2-80 x3+0 x4+0 x5+0 x6-3X|一 马 七+X4=-2-4元 一 九2 +尤5=4stx2%|2%2 2七+/=-3xi 0,

41、z=123,4,5,6对偶单纯形法得到的初始单纯形表Xb-60 X-40 x2-80 x30X40 x50 x6bX4-3 e-1-1100-2X5-4-1-3010-4/-2-2-2001-3a-60-40-80000以-3 0为轴心项,换基迭代得Xb-60斗-40 x2-80130%0 x50X6b玉12/31/3-1/3002/3X505/3-5/3-4/3 410-4/340-2/3-4/3-2/301-5/3cr00-60-2000以-4/3 6为轴心项，换基迭代得X,-60 xi-40 x2 -8()X30尤4。无6bX|11/43/40-1/401X40-5/45/41-3/40

42、1%0-3/2 -1/30-1/21-1(T0-2 5-3 50-1 50以-3/2 8为轴心项，换基迭代得Xb-6 0 x-4 0 x2-8 0 1 30%0 1 50%6b王104/93/4-1/1 2-1/1 25/60055/3 61-3/4-5/61 1/6%2012/901/3-2/32/3CT00-2 6 0/90-2 0/32 5全部的检验数b NO,得到最优解为(5/6,2/3,0).(3)对偶模型化为标准型得ma x。=2 y 1+4 y 2 +3 y3+0 y4+0 y5+0乂3%+4为+2%+治=6 0*2%+丫2+2乂+丫5=40s t.0,z=l,2,3,4,5,6

43、初始单纯形表为yB2券4 y 23%30%0儿b%3431006 0K2120104 0了61320018 0CT243000以3为轴心项，换基迭代得yB2 V4 y23y30y506b14/32/31/30020%0-5/32/3-2/3100%05/34/3-1/30060a04/35/3-2/300以4/3 0为轴心项，换基迭代得yB2 y4 y23y30%06b为3/411/21/400155/403/20-1/41025儿-5/401/2-3/40035(T-4/301-100以3/2为轴心项，换基迭代得2yl4 y23%0%0%b力1/3101/3-1/3020/35/601-1/

44、62/3050/3儿-5/300-2/3-1/3085/3CT-13/600-5/6-2/30由全部检验数b 0,得最优解为(0,20/3,50/3)o(4)比较第五届1.某公司制造甲、乙两种产品，甲、乙两种产品的产量每天分别为3 0 个 和 1 2 0 个。公司希望了解是否通过改变这两种产品的数量而提高公司的利润，制造每个产品所需的加工工时和各个车间的加工能力如表5-1 0 所示。表5-1 0产品的相关数据车间产品甲产品乙车间能力(每天加工工时数)1203 0 02035 4 03224 4 041.213 0 0利润/每个产品(元)5 0 04 0 0假设每天甲、乙产品的生产产量分别为：可

45、，2,则线性规划模型为max z=500X+400 x22/3003X2 540stx 2XI+2X2 4401.2XI+1.5X20使用QM软件求解并回答下面问题。(1)最优解是什么，最大利润是多少?(2)哪个车间的加工工时已用完？那个车间的加工工时还没用完？其松弛变量即没用完的加工工时各为多少？(3)四个车间的加工工时的对偶价格各为多少？请对此对偶的含义予以说明。(4)如果请你在这四个车间中选择一个车间进行加班生产，你会选择哪一个？为什么？(5)目标函数中西的系数在什么范围内变化时，最优解不变。(6)目 标 函 数 中 的 系 数 从 4 0 0 提高到4 9 0 时，最优解变了没有，为什

46、么？(7)请解释右端常数项各值的上限和下限。(8)车 间 1 的加工工时数从3 0 0 增加到4 0 0 时，总利润能增加多少，这时最优解变化了没有？(9)车间3 的加工工时数从4 4 0 增加到4 80 时，能否求得总利润增加的数量？为什么？解：(1)将原模型变换成标准形maxz=500%1+400 x2+0 x3+0 x4+0 x5+0 x62x,+七=3003 九 2+Z =540st.0,z=1,2,34,5,6 2 0 1 0 0 0(300、0 3 0 1 0 0 540,/A=,b=2 2 0 0 1 0 440J.2 1.5 0 0 0 1J 1300,取B=(P3 p4 p5

47、 26)为可行基，则gC-CBB A C,得到最初单纯形表为：)C=(500 400 0 0 0 0)=(0 0 0 0),CBB b=0,B-A A,CBXB500%!400X20*30 x40 x50犬6h0当2010003000九40301005400%22001044001.21.50001300%-5004000000500100.50001500匕030100540002-1010140001.5-0.6001120%-ZJ0400-250000500100.50001500&001.51-1.50330400 x201-0.500.50700000.1 50-0.7511 5%-

48、Z j00-5 00-2 0 00最优解为：/=1 5 0,x2=70最大利润：m a x Z =5 0 0 X 1 +4 0 0 x2=5 0 0 x 1 5 0 +4 0 0 x 70 =1 0 3 0 0(2)由最终单纯形表知：3=与=，匕=3 3 0,4=1 5,因此，一车间和三车间的加工工时已用完，二车间和四车间没有用完，分别剩余3 3 0和1 5个加工工时。(3)由最终单纯形表知：第一车间的影子价格为(5 0),即5 0,第二车间的影子价格为-(-2 0 0),即2 0 0。这表示在一定范围内，第一车间每增加一个设备台时,目标函数增加5 0；第二车间每增加一个设备台时，目标函数增加

49、2 0 0。(4)选择第三车间，因为第三车间的影子价格高，每增加一工时带来的利润大。士的系数为基变量系数，因此，设：，的波动为；I,令。=5 0 0+4,要使优解不变，贝I J：(5)由最优单纯形表知：C=(50 400 0 0 0 0)，CB=(5 0 0 +2 0 4 0 0 0)；1 0 0.5 0 0 0、0 0 1.5 1 -1.5 00 1 -0.5 0 0.5 0B-A=0 0.1 5 0 -0.75 1,OC-CBB-A 0t(5 0 0 +2 4 0 0 0 0 0 0)-(5 0 0 +2 0解得：A 4 0 0即:100.5000、4 0 0 0)0 01.51-1.50

50、00 1-0.5 00.501 0 0.1 5 0-0.75(6)设 的 波 动 为4,令，2工0 0+；1,若使最优解不变，贝 小C-CBB-A Ot即:1 00.5000)(5 0 0 4 0 0+/1 0 0 0 0)-(5 0 0 0 4 0 0 +2 0)00011.5-0.510-1.50.500解得：-4 0 0 2 1 0 0,2 -1 0 0.-.0 c2 0,即：、0.1 5 0 -0.75 1,、3 0 0 ,0解得：-1 0 0 A 1 4 0,v 3 =3 0 0 +4,.2 0 0 W仇4 4 4 0同理：分别令 b?=3 0 0 +4,b?=3 0 0 +4,=3

51、 0 0 +4；解得：0 2 G 2 1 0,+8),3 0 0 b3 4 6 0 ；b 4 G 2 85,+8)。(8)4 0 0在常数项变化范围(2 0 0,4 4 0)之间，因此，总利润变化量:5 0 x(4 0 0-3 0 0)=5 0 0 0；最优解变化为：不能，因为常数项变化超出其变化范围(3 0 0,4 6 0)2.已知线性规划问题：m a x z =项 +2X2-2%|+W 2s tx-x,+2X7 7 0的最终单纯形表如表5-u所示。表5-1 1最优单纯形表CBXB2X20 x30 x40 x5b2010%X511000130001_%3CZj000-1-2(1)写出其对偶模

52、型；(2)求出对偶模型的最优解；(3)写出最优基5及其逆矩阵5”；(4)若右端项变为=(2 J 2,2)，最优基是否变化？求出变化后的最优解及其最优值。解：(1)其对偶模型为:min co=2yx+7%+内,2%一乃+为 Ist.y+2y2 2 2，乃，为2原模型最优解为：(3,5,3,0,0)，设对偶模型最优解为Y*Xs=,知 匕=；设对偶模型的剩余变量为匕，%由犷=0知：3匕+5 y 5=0,由于剩余变量均为非负，故 匕=0，八=0,此时对偶模型的约束条件为:r；=o的最优解为:y；=2丫；=iYl-0 Y2 1 Y3-2 匕=0,2匕J -1/2 3/2,(4)常数项波动变化，当b,变化

53、时，只要8-%20,则8仍是最优基。令 瓦=2 +4,b2=7+A2)b3=3 +4则：5 b 0解得：4 G -1,+8)4 -3,13 ij b+o o)当常数项b=(2,12,2)在其变化范围中变化，故最优基不变；最优解为(2 6 0,2,0)、最优值为14。3.给出了下列线形规划：m a x z =6 2 +2x2+12 x3 54工1+3/2 4s tx 2x1+6X2+3X3 0的最优单纯形表如表5-12所示。表5-1 2最优单纯形表4Xb6%j2X212/0 5,O s 2b12七4313 1J1080S?-250-116CJ-ZJ-10-20-40(1)求出最优基不变的灯的变化

54、范围；(2)求出最优解不变的 3的变化范围；(3)在原线性规划的约束条件上，增加下面的约束条件：+22+2/4 12其最优解是否变化，如变化，求出最优解。B 解：设b 2的变化为b z+L1/3 0、-1 b只要5上2 0,则b仍为最优基妹心北4层)2 -6,即：0b2+2 2 4 ,即为在 2 4,+8)上变化是最优基不变。(2)设C 3的变化为。3+九，要是最优基不变，则C-CB8 T A 4 0,即：、/4/3 1/3 1 1/3 0)(6 2 12 +Z 0 0)-(12 +Z O j 2 5 0 1 =(-10-4 2/3 -2-2/3 0 -4-2/3 0)0/.A 2 6C 3

55、+4 2 6即当C 3在 6,+0 0)上变化时，最优解不变(3)其最优解变化为(0 0 6 6 1 2)4.有一标准型的线性规划问题：m a x z =CXAX=bs.t X 2 0其最优单纯形表如表5-1 3所示：表5-13 最优单纯形表cb Xq x iC/2C4X4bq10-13-11%012-11200-3-3-1z =8其中：*4,%是对用于初始单位矩阵的松弛变量。试求:(1)利用最优单纯形表求夫，,2，3，。4，。5。（2）假定用b+幺 代替力，其中（1人-c o 2 +c o,要使现行最优基5保持不变，力的变化范围？当=5时，求最优解。（3）求约束影响价格。解（1）从最优单纯形

56、表中得出：（3 -1、夕匕1-1 1）由于,%是松弛变量所以。4,均为0。根据巴 工-C QA知：（0 -1 3（C,G,C3,C4,C5）-（C（,C,）n,=（0,0,-3,-3,-1）1 0 1 2 -1 1 ）得出：。|,，2，。3，。4，。5 分别为 2,3,1,0,0 on+/i（2）要使最优基不变，则应0,即1 1 1 2-4）却 得出:一 A A =4 2。当 2 ,在区间内，最优基不变，最优解为：3 3（XI,X2,X3,X4,X5）T=（-,-,0,0,0）T（3）根据影子价格与松弛变量之间的关系知：必=3,%=15.有最大问题的最优单纯形表如下，其中乙，为松弛变量。表5-

57、14最优单纯形表X x2 x3 x4 x50 -1 1 3 11-10-10240-3 0-3 -1写出该问题的最优解。当 为 何 值 时，其对偶问题无解？并说明理由。解（1）由以上的最优单纯表得出最优解为：（X|，X 2，X 3，X 4，X 5）T =（4,0,2,0,0）T（2 ）若 原 模 型 有 可 行 解 但 目 标 函 数 值 无 界，则 对 偶 模 型 无 解。设=（。，。2，。3，。4，。5）,因为“C 5 为松弛变量，所以均为0 .0 -1 1 3 11 -1 0 -1 0解得：Cl=0,C2=-4,C3=l设 C3J3+A C 3,当 c-g B a 时，最优基不变，即 C

58、-g B =(,4 1+a 3,f o -1 1 3 C0,0)-(1+A c3,0)1-1 0 -1ft?W：-lA cJ3 BP-1AC33时，最优基不变。此 时 叫 J?G Pl=-4-(C3 +C3,0)V=-3+C3当 巴 对 且-上 八。3与 时，原模型有无界解，即八。3=3时，对偶模型无可行解。6.考虑下列线性规划：max z-5A：|+5 x2+13 x3-X +x2+3X3 2 012 x 1+4X2+10元3 0,i=1,2,3最优单纯形表如表5-15所示：表5-1 5最优单纯形表X x2 X3 x4 x5X2X5-1 1 3 1 016 0 -2 -4 12 0100 0

59、-2-5 0(1)写出此线性规划的最优解、最优基5和它的逆S T；(2)求此线性规划的对偶问题的最优解；(3)试求,2 在什么范围内，此线性规划的最优解不变；(4)若 4 =2 0 变 为 4 5,最优解及最优值是什么？解(1)由最优单纯形表知：最优解为(占，入 2，%3，4，/)T=(，20,0,0)T1 04 11 0-4 1(2)因为对偶模型的最优解是原模型松弛变量检验数值的相反数，所以，对偶模型的最优解为：必=5,%=0。(3)设 C 2=C 2+4,C2是基变量对应的系数，要使原模型的最优解不变，则C-CRB A o,即（-5,5+2 13,0,0）-（5+,加）-1J 63 1 0

60、-2-4 J o102 13 2 0 c 0,解得:-20 2 -2即重新用单纯形表解得集7.分析线性规划mas t.解：化为标准型：ma x z(6)=(3+：玉 +X3=St J 2X;9+兀=3须 +2X2+x5Xj=p 0A=0 2、3 2单纯形表如下：450b.,2。若 仇=2 0变为全优解为（0，0,9）T,最优值;可题中e变化时最优解变化情况：x z ）=（3+26）X+（5-0）x2x42X2 123工1+2X2 0的+（5-。）工2+O X3+0 x4+412=181 0 00 10/7=0 0 1J45,最优基发生变化，将45代入瓦,为 117。9於0)o%5(e 0)4、

61、12J 8)C=(3+26,5 。,0,0,0)CBXB(3+2。)占（5 8）40X30X40*5b0X31010040X402010120X5320011803+2。5-0000以1为轴心项，换基迭代得:CBXB（3+2 6）X(56)Z0%30%0%b3+2。X1010040%02010120*502-3016（J05-6-3-2000-1 2-8。当e 5时，。o,此 线 性 规 划 模 型 有 唯 一解，最 优 解 为(X1,X2,X3,X4,X5)T=(4,0,0,12,6)T。当。=5时，%=0且对应的列存在正数，有无穷个解。当。0,以2为轴心项，进一步换基迭代，得:CBXB(3

62、+2。)*(5-。)0“30X40%5b3+2。王10100400031-165-0X201-3/201/23a0021 1。2 20-+-02 2-2 7-5。由 于 5,则。0,此 线 性 规 划 模 型 有 唯 一 解，最 优 解 为：(XI,X2,X3,X4,X,)T=(4,3,0,6,0)T8.现有线性规划问题ma x z=-5xj +5 +13七一 项+3尤3 20s t.12%+4X2+10 x3 0先用单纯形法求出最优解，然后分析在下列各种条件下，最优解分别有什么变化？(1)第一个约束条件的右端常数由常数20变为30；(2)第二个约束条件的右端常数由常数9 0变为70；(3)目

63、标函数中冗3的系数由13变 为 8；(4)司 的 系 数 歹 晌 量 由 变 为(5人(5)增加一个约束条件2尤 1 +3 2+5巧 4 5 ；(6)将原来第二个约束条件改变为1 0 xi+5叼+1吗 100解：单纯形法求得最优单纯形表为Xb-5 x5X213“30X40X5b 由X2-11310表用得，20最 优 解X5160-2-4110 为(0,500-2-5020,0),B=p 0、(P i,Ps),B-1=1一4 1,(i)设 仇 波 动 为 4,oIl B1 仇=1 0、一 4 1；(20+4 190 J/2 0+4、=1 1 0-4 4 八0,得-20 A 2.2 5,即 0 仇

64、22.5时最优解不变。所以当从20变 为 30时，最优解已经改变为(0,0,9)op 0俨(20、设”波动为。,由于 屹=1-4 1八 90+4 乂1。+4 八 0,得 为 N 1 0,即匕 2 2 8 0 时最优解不变。所以当坊从90变为70时，最优解已经改变为(0,5,5)。(3)由8=(P i,5)知 为 非 基 变 量 系 数，其变化幅度时，最优解不变。所 以 当 从 13变为8 时，2=8-13=-52,最优解不变。(4)1 H当占系数列向量由(12 J 变 为 时，最优单纯形表为XhX20131020 41表可知，%10-2-411 0 最 优 解5-50-2-50。为（0,20,

65、0）o(5)增 加 约 束 条 件2 6+3超+53 45后，模型变为ma x z=-5玉+5 x2+13x3X|+&+3工3-2012xl+4X2+10 x3 9 02x+3X2+5.0最优单纯形表为Xb-5七5 X213 x30X40X50%6bX3-5/4013/40-1/45/2X527/200-5/4127/640/3X233/1210-5/403/425/2（y-5/200-7/20-23/6由 表 得 最 优 解 为(0,25/2,5/2).条件改变后模型变为ma x z=-5%1+5 x2+13x3一 再 +%+3X3 20st.1 O x,+5X2+1 0 x3 0最优单纯形

66、表为Xb-5/5 X213X30X40%5b-1131020X2150-5-500500-2-50最优 解 为(0,0,0)。9.求最大化线性规划的模型的最初始单纯形表及最优单纯形表如表5-16及5-17所示。(1)填写最优表5-17中空白处的数字。(2)写出原线性规划问题。(3)写出其对偶线性规划模型及其最优值。(4)当方变为方+*其中=(1-1 )，,问丸在什么范围内变化，原最优基不变？(5)目标函数3的系数从一1变为一2,原最优基是否会改变？求出,2=-2时最优值。表5-16最初单纯形表CBXB2%一b 2*0%40%0%b0311100打0*1-12010“0%11-1001/b j2-11000表5-1 7最优单纯形表CBXB2%1%7530 x4050%b0-1-2152121210-1x2,12125解(1)填入数字后，单纯形表为CXB2%_ 1%2lx30 x4OX50尤6b0 x40011-1-2152101/20121210-101-3/20125b j00-3/20-3/2-1/2(2)原线性规划模型为ma x z=2不一st.3%+x2 4-x3 50X1 一