考研数学知识点总结-高等数学

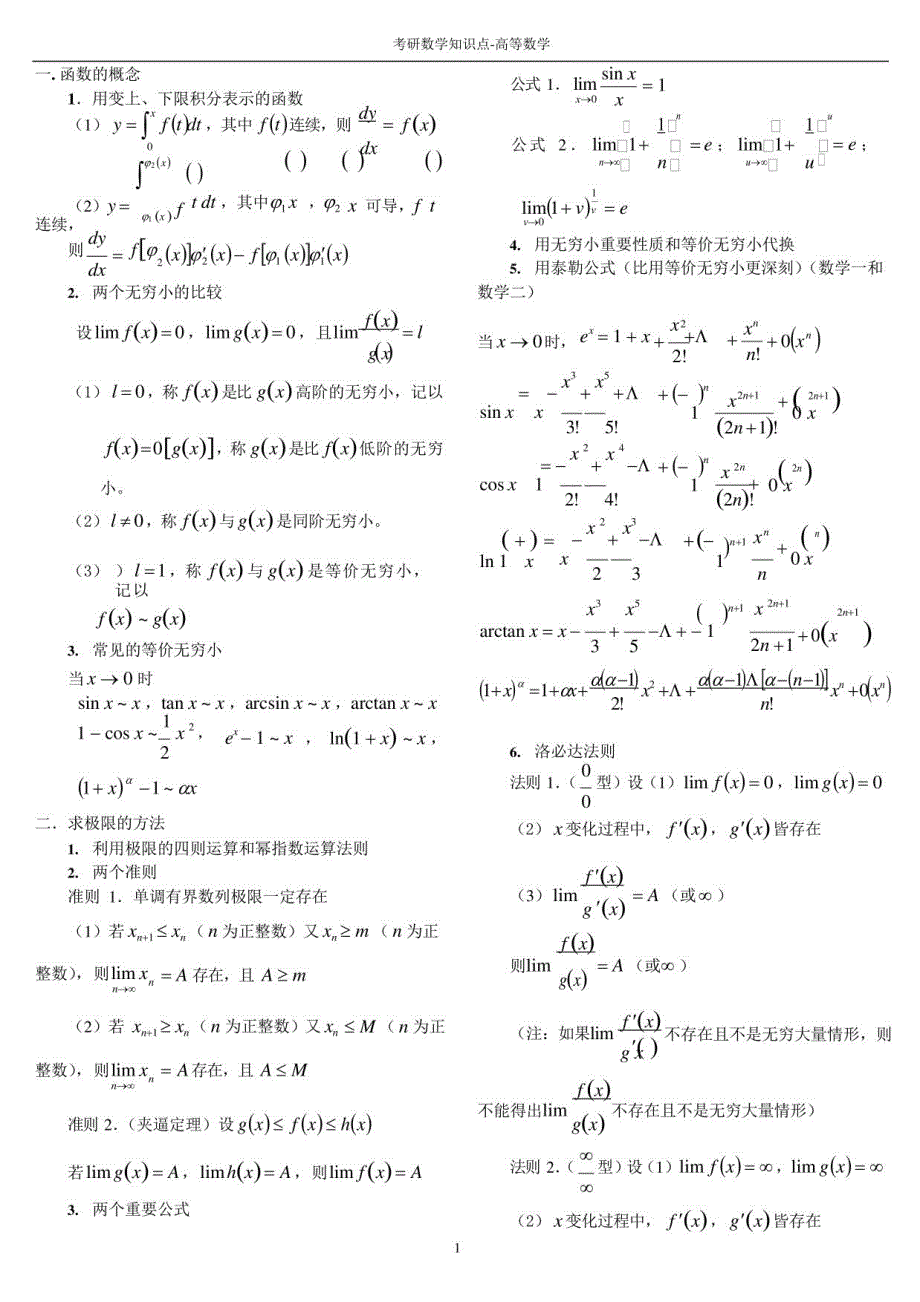
《考研数学知识点总结-高等数学》由会员分享，可在线阅读，更多相关《考研数学知识点总结-高等数学（38页珍藏版）》请在装配图网上搜索。

1、考研数学知识点-高等数学函数的概念1.用变上、下限积分表示的函数(1)y =其中/连续，则 加=/(x)(2)f t d t,其中9|X，(p2 x 可导，/t连续，则 包d x/M(M M (%)-/fe (x)以(X)2.两个无穷小的比较公式 1.1*-0 X i tf公式 2.li mQ|l+_ =e；li m-n fili m(l+v)v=e4 .用无穷小重要性质和等价无穷小代换5.用泰勒公式(比用等价无穷小更深刻)(数学一和数学二)e-1+设li m/(x)=O,li mg(x)=O,且li m且 口=/4 3(1)/=0,称/(x)是比g(x)高阶的无穷小，记以/(x)=O g(x

2、),称g(x)是比/(x)低阶的无穷小。(2)/00,称/(x)与g(x)是同阶无穷小。(3)1=1,称/(%)与g(x)是等价无穷小,记以/C O g(63.常见的等价无穷小当x f 0时si n x x,tan x x,ar c si n x x,ar c tan x x,1 2,、1 -c o sx,x e-1 x,ln(l+x)x,(1 +x)a 1 (XX二.求极限的方法1.利用极限的四则运算和某指数运算法则2.两个准则准 则1.单调有界数列极限一定存在(1)若(为正整数)又x,?加(为正整数)，则li mx“=A存在，且A 2机?：00(2)若尤.e x,(为正整数)又/KM(为正

3、整数)，则li mx“=A存在，且A 4MW 3 0准则2.(夹逼定理)设g(x)/(x b M x)若li mg(x)=A,Ii m/i(x)=A,则li m/(x)=A3.两个重要公式光3 x5(严 x2,1+1ar c tan x-x-1-A +-13 5 2/7 +1(1+染=1+如当心+A+雇必精期+收)6.洛必达法则法则 1.型)设(1)li m/(x)=0,li mg(x)=00(2)无变化过程中，g(x)皆存在f(x)(3)li m z、-A(或8)g(x)f(x)则li m/、=A(或8)f(x)(注：如果li m不存在且不是无穷大量情形，则g.()iXd不能得出li m/、

4、不存在且不是无穷大量情形)法 贝！J 2.(二 型)设(1)li m/(x)=o o ,li m(x)=o o0 0(2)元变化过程中，r(x),g (x)皆存在考研数学知识点-高等数学f(x)(3)li m,、=A(或o o )8(x)则li m=A(或8)7 .利用导数定义求极限+Ax)-f(x)基本公式：li m Ar-0=r G)o 如果存在8 .利用定积分定义求极限基 本 公 式 顺 不 x d x 如果存在三.函数的间断点的分类函数的间断点分为两类:(1)第一类间断点设%是函数y=/(x)的间断点。如果/(x)在间断点X处的左、右极限都存在，则 称X是/(X)的第一类间断0 0点。

5、第一类间断点包括可去间断点和跳跃间断点。(2)第二类间断点第一类间断点以外的其他间断点统称为第二类间断点。常见的第二类间断点有无穷间断点和振荡间断点。四.闭区间上连续函数的性质在 闭 区 间 力 上连续的函数/(X),有以下几个基本性质。这些性质以后都要用到。定 理1.(有界定理)如果函数/(X)在闭区间卜,“上连续，则/(尤)必在。力 上有界。定理2.(最大值和最小值定理)如果函数/(x)在闭区 间 句 上 连 续，则在这个区间上一定存在最大值M和最 小 值m o其中最大值M和最小值，”的定义如下：定义 设/(工0)=加 是区间。,以上某点而 处的函数值，如果对于区间 a,b上的任一点x，总

6、有f(x)0,a w 1)xln ad xd l og “x =(a 0,a w 1)x l na(in x)=-d In x=d xx x(优)Ina (a 0,o w 1)d ax=ax In ad x(a 0,a w 1)2考研数学知识点-高等数学9)金d e =e d x a r cs inx)=一d a r cs in x=ax7 1-%27 i-%2fa r ccos x)=-,7 7 1-%2，1d a r ccos x=i,-rd x7 i-x2(a r ct a nx)=+/c l a r ct a n x =.2d x1 +x()=一d are cot x-d x(J_ _

7、 _1+x2In x +y/x 2+a2=-V 72+a2dl n(x+Vx 2+a 21=.d x /2,2V x+c i，l n(.r+5/x2-a2)l =-d In(x +Jx 2 _ q 2)_ .,否2 .四则运算法则/(x)g(x)=r G)g (x)f/(x)g(x)=f(x)g(x)+f(x)g(x)价=陨)冷 蕾)如)的“0)-J3 .复合函数运算法则设y =/()，u=(p(x),如果p(x)在x处可导，f(u)在对应点“处可导，则复合函数y=/次力 在x处可导，且有d y =d y d u=丹 加)”(x)d x d u d x对应地办=/()疝=/曲0。(1)公由于公

8、式办=不 管”是自变量或中间变量都成立。因此称为一阶微分形式不变性。4 .由参数方程确定函数的运算法则设x =加)，y=件(f)确定函数y=)(x)，其中夕(。，什)存在，且9 (f)w O,贝Jd x o。)二阶导数d y =d如 工 dxXif _ _ _”-3”d x2 d x d t 曹 。F5 .反函数求导法则设y=/(x)的反函数x =g(y),两者皆可导，且则(r(x“0)f (x)J 1 /二阶导数 g (y)=&6*=.Ld y d x 3d x_ r(x)_rW l(x。)(班 加36.隐函数运算法则设y =y(x)是由方程网m)=0所确定，求 的方法如下：把F(x,y)=

9、0两边的各项对尤求导，把y看作中间变量，用复合函数求导公式计算，然后再解出y 的表达式(允许出现y变量)7 .对数求导法则先对所给函数式的两边取对数，然后再用隐函数求导方法得出导数o对数求导法主要用于：暴指函数求导数多个函数连乘除或开方求导数关 于 暴 指 函 数 =/(刈 的 常 用 的 一 种方法3考研数学知识点-高等数学/(X)在X。处可微O/(X)在X。处可导。y =这样就可以直接用复合函数运算法则进行。8.可微与可导的关系(1)在 闭 区 间 句上连续；(2)在开区间(见匕)内可导；9.求阶导数(2 2,正整数)先求出y ,y ,A,总结出规律性，然后写出y(n),最后用归纳法证明。

10、有一些常用的初等函数的阶导数公式(1)y=d y()=e则存在Je(a,b),使得牛 皿/b-a或写成/(。-/(a)=(ab)有时也写成/(JC0+A r)-/(x0)=尸(%+如 力AY(2)y =(0,a w 1)y()=a (l n y(0 6 =co s Qx+,丁口推论1.若/在(。力)内可导，且广(x)三0,则/(x)在(a,8)内为常数。(5)y =n x y()=(-1产(_1)!婷两个函数乘积的n阶导数有莱布尼兹公式()()=*)()(4)()U XV X Z X V Xk=0推 论2 .若/(x),g(x)在(。为)内 皆 可 导，且f(x)=g r(x),则在(a,b)

11、内f(x)=g(_ r)+c,其中 c 为一个常数。三.柯西中值定理(数学四不要)其中小出)!()设函数f(x)和g(x)满足：(1)在闭区间3,口上皆连续；)(X)=v(x)假设“(X)和u(x)都是阶可导。(2)在开区间(a,。)内皆可导；且g(x)W0微分中值定理罗尔定理设函数/(X)满足则存在J w (a,b)使得g(b)-g(aY g，(D(1)在闭区间 a,。上连续；(注：柯西中值定理为拉格朗日中值定理的推广，特殊情形g(x)=X时，柯西中值定理就是拉格朗日中值定(2)在开区间(a,6)内可导;理)f(a)=f(b)四.泰勒定理(泰勒公式)(数学一和数学二)则存在J e(。力)，使

12、得/(J)=0拉格朗日中值定理设函数/(X)满足定 理1.(皮亚诺余项的阶泰勒公式)设/(X)在X。处有阶导数，则有公式/(X)=/(x )+-X )+-x 7)；A+-X )+R(A)0 1!0 2!0 n!0 4考研数学知识点-高等数学G-Xo)其 中 H“(x)=o (x%)(x f X o)称为皮亚诺余项。l i m/邕=W/)前面求极限方法中用泰勒公式就是这种情形，根据不同 情 形 取 适 当 的n ,所 以 对 常 用 的 初 等 函 数 如e”,s i n x,co s x,l n(l +x D(l+x)”(为实常数)等的阶泰勒公式都要熟记。定 理 2 (拉格朗日余项的阶泰勒公式

13、)设/(x)在包含/的区间(a,b)内有+1 阶导数，在a,b上有阶连续导数，则 对x G a,b,有公式()=()+血1 1(_)+曰叫 _ +A+，(/)(-)、()fx f)二门-1 2其 中R (x)=彳;胃p(X 一 看 尸，(J在无0 与龙之间)称为拉格朗日余项。上面展开式称为以与为中心的阶泰勒公式。当x 0=O 时，也称为阶麦克劳林公式。如果l g 7?“(x)=0 ,那么泰勒公式就转化为泰勒级数，这在后面无穷级数中再讨论。导数的应用：一.基本知识1 .定义设函数/(X)在(。/)内有定义，X。是(。力)内的某一点,则如果点看 存在一个邻域，使得对此邻域内的任一点X(X H X

14、o)，总有/(X)/(X o)，则称/G o)为函数/(X)的一个极大值，称 x0为函数/(X)的一个极大值点；的一个极小值，称 X。为函数/(X)的一个极小值点。函数的极大值与极小值统称极值。极大值点与极小值点统称极值点。2 .必要条件(可导情形)设函数/(X)在X。处可导，且 X。为 了(X)的一个极值点，则/,(xo)=O 我们称x满足f x0)=0的%为/(%)的驻点可导函数的极值点一定是驻点，反之不然。极值点只能是驻点或不可导点，所以只要从这两种点中进一步去判断。3 .第一充分条件设/(X)在x处连续，在0 0 ,而在(工 0，%0 +b)内的任一点X 处，有/(x)0，则f(x0)

15、为极大值，与 为极大值点；2 如果在(%)内的任一点x处，有/f(x)0 ,则f(xQ)为极小值，与为极小值点；3 如果在(/一 d,x0)内与(/，/+d)内的任一点x处，/(X)的符号相同，那么/(%)不是极值，无。不是极值点。4 .第二充分条件设函数/(x)在 与 处有二阶导数，且:(x 0)=0,尸(%)#0,则如果点与 存在一个邻域，使得对此邻域内的任一点x(x 声 /)，总有/(x)/(%0)，则称/(%)为函数/(X)当/(/)0时，/(曲)为极小值，与 为极小值点。5考研数学知识点-高等数学二.函数的最大值和最小值y=/(x)在(。,内是凸的。1.求函数/(x)在 上 的 最

16、大 值 和 最 小 值 的 方 法求曲线y=/(x)的拐点的方法步骤是:首 先，求 出/(x)在(。力)内所有驻点和不可导点 第一步：求出二阶导数尸(x)；X,A,x*,其次计算/(%(),A,f(xk),f(a f(b)o最后，比较/(xJ,A其中最大者就是/(x)在1力 上的最大值M；其中最小者就是/(x)在 上 的 最 小 值m 2.最大(小)值的应用问题首先要列出应用问题中的目标函数及其考虑的区间，然后再求出目标函数在区间内的最大(小)值。三.凹凸性与拐点1.凹凸的定义设/(x)在区间/上连续，若对任意不同的两点用,七，恒有兀 上 山 一 1 y(x)+/(x 池 胫 与 当 、xk；

17、第三步：对于以上的连续点，检验各点两边二阶导数的符号，如果符号不同，该点就是拐点的横坐标；第四步：求出拐点的纵坐标。3.斜 渐 的若limX4a则x=a为曲线y=/(x)的一条垂直渐近线。2.水平渐近线若 lim f(x)=b,或 lim f(x)=bXT+00 X T-8则y=。是曲线y=/(x)的一条水平渐近线。国S (%)-=blim /(%)-ax=bX T-8则y=办+8是曲线y=/(x)的一条斜渐近线。五.曲率(数学一和数学二)设 曲 线y=/(x),它 在 点M(x,y)处 的 曲 率k=一工 _ _ _ _ _若A Y 0,则称R=L为点M(x,y)处1+平 卜的曲率半径，在M

18、点的法线上，凹向这一边取一点。，使|AW|=A,则称D为曲率中心，以D为圆心，R为半径的圆周称为曲率圆。不定积分一.基本积分公式a+11.xadx=+C(a l,实常数)如果在(。为)内的每一点x,恒 有/(无)O,aw l)J I n aex d x=ex+C4.j co s xd x=si n x +C5.j si n xd x=-co sx +C6,xd x=t an jc+C7.,e sc2xd x=J 2 d x=-co t x +CJ J s m x8.jt an x s ecx dx =s ecx +C9.jco t x cs cx dr =-cs cx 4-C10.j t an

19、 A ZZV=-I n co s x|+C11.j co t xd x=ln|s i n x|+C12.js ecx dr =ln|s ecx+t an x|4-C13.j es c xd x=ln|cs c x -co t x|+C1一4.r d x.x .zz_=ar cs i n +C Q0)aj-d x 1 x xr(。)15.r =_ ar ct an _+CJ a2+x2 a a“二，留+。(Q)6二.换元积分法和分部积分法1.第一换元积分法(凑微分法)设=尸()+C,又e(x)可导，贝IJ夕(天)J/%)(x)g 7%)刎工)f(u)d u=F(u)+C=F(p(x)+C是非常熟

20、练地凑出微分。常用的几种凑微分形式：(1)j f(ax+b)d x=，J /(+b)d(ar +b)(a 丰 0)(2)jf(ax+b)x,-d x=y a xn+b)d(ax+bt(a#0,#0)(3)J/Q n x)f(n x)d(i n x)(4)尸二&二,尸 婷 三f-fJJ x 1 J/)$=2j 7(4)d G)(6)f(ax)axd x=y(a)d(相)(a 0,a N 1)J.G)e d =J.G)e,)(7)j/(s i n x)co sxd x=J/(s i n x)d(s i n x)(8)j/(co s x)s i nxd x=-j/(co sx)d(co s x)(9

21、)j/(t an j;)s ec2 xd x=J /(t an x)r f(t an x)CI O)J /(co t x)cs c2 xd x=-j/(co t x)j(co t x)1)j/(s ec x)s ec x t an xd x=j/(s ecx)d(s ecx)(1 2)J/(cs cx)cs cx co t x(i x=-j/(cs cx)j(cs cx)(.)(13)J .fcs i n x&=J /(ar cs i n x)d(ar cs i n x)(1 4)，。:公=-J/(cco sx)d(ar cco s x)4)(1 5)J 黑 x)公=J f(ar ct an

22、x)d(ar ct an x)f(ar cco t x)“_ /(ar c co t x)d(ar c co t x)(J 1+/一17考研数学知识点-高等数学这里要求读者对常用的微分公式要“倒背如流”，也就8考研数学知识点-高等数学(17)f ar ct an目in X1 +x2d x=-1 /1 ar ct an 1巨质ar ct an -：18).=J (+Inx川(+yjx a d n x(a 0)()dx=19ylx2-a2jx2-a1)/(l n Q+Jx 2 _ 2)(a 0)(20)=W(x)+C (/(x)#0)X口).2人 2 1然后再作下列三种三角替换之一:根式的形式所作

23、替换三角形示意图(求反函数用)x=a si n t卜y/a2+x2x=a t an ta/2 2y/x-a x=a s ec t上A3,分部积分法-(一)20X口 (/ln(x+2 22.第二换元积分法设(x),v(x)均有连续的导数，则设 x =9(r)可导,且 d(/)w 0 ,若 J(x)dv(x)=(x)v(x)-J v(x)d“(x)J.fM)e(r)r=G(r)+C,或 J(x)M(x)dx =(x)v(x)-J/(x)v(x)dx则_ _ _ _ _ _ _Q _ 使用分部积分法时被积函数中谁看作w(x)谁看作J 9 f(p(t)(/)J r=G(r)+C=G夕 1(x)+CM(

24、x)有一定规律。其中f =，(x)为x=(/)的反函数。第二换元积分法绝大多数用于根式的被积函数，通过换元把根式去掉，其常见的变量替换分为两大类：第一类：被积函数是x与 弧+6或x R 士9或由构成的代数式的根式，例 如y jae+b等。只要令根式板声=，解出x =9。)已经不再有根0式，那么就作这种变量替换x=e r即可。第二类：被积函数含有/4%2+&+。(AHO),如果仍令解出x =0时先化为JA(X_X0)1，A 0 时，先 化 为(1)P P(x)s i n ax,P(x)co s ar 情形，n n nP.(x)为几次多项式，。为常数，要进行次分部积分法，每次均取e s i n c

25、ue,85就为丫。)；多项式部分为u(x)(2)P(x)ln x,P(x)ar cs i n x,(x)ar ct an x 情形，P“(x)为n次多项式取P“(x)为v (x),而I n x,ar cs i n x,ar ct an x为 (x),用分部积分法一次，被积函数的形式发生变化，再考虑其它方法。(3)e。s i n次，eco s fo x情形，进行二次分部积分法后要移项，合并。(4)比较复杂的被积函数使用分部积分法，要用凑微9考研数学知识点-高等数学分法，使尽量多的因子和d x凑成定积分的概念与性质1.定积分的性质 =f xd x(2)/(x)tZr =0(3)L /(x)+k2f

26、2(x)d x=k J (x)右+A 2f f i(x)d x；o ；o ；o (4)f f x d x=f x d x-f x d x(c 也可以在 a,bJa Ja Jc之外)(5)设/(x)g(x)(7 X /?),则/(X)公 W/g(x)dxa a(6)设a。，m f(x)M (a x b),贝Um(b-a)f(x)d x M (b-a)(7)设a b,则 J/(x)i A-f(x d x(8)定 积 分 中 值 定 理 设/(x)在。,句上连续，则存在J e,b ,使定义：我们称 一/粒 为/(x)在 口,同上的积b-aa分平均值(9)奇偶函数的积分性质_|_ f x)d x=0(

27、/奇函数)-aa f(X)d X=2f f(X)d x(/偶函数)|Jox e a,可称为变上限积分的函数定理：(1)若/(x)在 a,同上可积，则F(x)=在 a,句 上连续(2)若/(x)在 上 连 续，则F(x)于(。必在 a,可上可导,且F(x)=f(x)F(x)=p*1()(p(x),(p(x)推广形式：设 力，八 C可导，/(x)连续，则 F(x)=/M(x)M(x)丹臼(x)(x)2.牛顿一莱布尼兹公式设“X)在 上 可 积，“X)为/(x)在 a,句 上任意一个原函数，b也则有方/(X)公=/(丫=F(b)-F(a)(注：若/(x)在 a,句上连续，可以很容易地用上面变上限积分

28、的方法来证明；若/(x)在口上可积，牛顿一莱布尼兹公式仍成立，但证明方法就很复杂)三.定积分的换元积分法和分部积分法1.定积分的换元积分法设/G)在 。,句上连续，若变量替换=C)满足(1)，(f)在 a,(或),a)上连续；(2)(a)=a,=b,且当 a W/万时，(10)周期函数的积分性质设/(x)以T为周期，a为常数，则C f dx =定义：设/(x)在 a,“上可积，则尸(x)=/(/,x)d x二.基本定理1.变上限积分的函数10考研数学知识点-高等数学a 夕(。b,则 bf(x)dx=武(。力a a2.定积分的分部积分法设M(x),u(x)在瓦|上连续，则|uxvx)dx-W(X

29、)V(J:)/,-j或 J uxdvx=w()v(x)/?-j vxdu(x)11考研数学知识点-高等数学定积分的应用.平面图形的面积1.直角坐标系模型 I S|=y2(X)-(x)d x其中 xe a,b模型n S2=广3-再 力其中尤2(y)&i(y)，y c,d 3.参数形式表出的曲线所围成的面积设曲线c的参数方程谿)(at(/)有连续的导数弧长S=优 广6出 击/x而dS=+也称为弧微分2.构坐标系设光滑曲线在a,上有连续导数弧长s =f加e)r+/(晒 四3.参数方程所表曲线的弧长设光滑曲线 c：x=K )(at y(t)在v (a,上有连续的导数曲线C的弧长S=j d t三.特殊的

30、空间图形的体积(一般体积要用二重积分)1.已知平行截面面积的立体体积设空间一个立体由一个曲面和垂直于z轴两平面z =c和z =d所围成，z轴每一点z(c z d )且垂直于z轴的立体截面的面积S(z)为已知的连续函数，则立体体积V 邛(z)d z2.绕坐标轴旋转的旋转体的体积(1)平面图形由曲线y =y(x)(2 0)与直线x =a,x =/?和x轴围成绕x轴旋转一周的体积12V n y 7(x)d x考研数学知识点-高等数学dV =2TT y (y)jy,I绕y轴旋转一周的体积Vv=I n xy(x)d x四.绕坐标轴旋转的旋转曲面的面积(数学一和数学二)(2)平面图形由曲线x =x(y)(

31、2 0)与直线y =c,y =d和y轴围成绕y轴旋际周的体积V=7T x y)d yy Je绕X轴旋转一周的体积设平面曲线C=3位于x轴上方，它 绕x轴一周所A n得旋转曲面的面积为S。1.设 A B的方程为 y =y(x)(a xb)则 S=2 力G)Ji+y(x)2 d x2 .设的极坐标方程为r=r(e),(0 )，(c r (/)力常微分方程二.变量可分离方程及其推广1.变量可分离的方程 方 程 形 式：=P(X)QG)()W O)d x(%(%)力0,M()”o)2.变量可分离方程的推广形式d y Ely 口(1)齐次方程 =/_ d x%令2=,xd y则 一d xd u=+X=d

32、 xr d uJ /(W)-M+c =In|%|+c/()13考研数学知识点-高等数学 户 户(2)一dy =z+、/w0,w0、)dx令 ar by+c=u,则 3 =a+bf()dxr _d_u_=f O=X +Ca+bfi)dy 4 y+q(3)-dx 马 x+b2y+c2j,b 当A=1 情 形，先 求a2见x+hy+c=i i i0孔（a 0）的解 ,“2工 +。2,+。2 二=0令=X-v-y-p则 一 一/舛 纳=/1%1属于齐次I _I 2 2 C l I)口2 2 U方程情形a h当=1 1 =0情形，2%令”b、则 办=/田 /x +仇y+a也-7(.x+b y)+c I

33、1 2口令 =”X+，du dy +J U则7 =4+仇14+。/jax ax _Au+c?属于变量可分离方程情形。三.一 阶线性方程及其推广1.一阶线性齐次方程+P（x）y=0dx2.一阶线性非齐次方程3 PG）y=Q（x）dx用常数变易法可求出通解公式令 y=C（x）e xdx代入方程求出C（x）则得 y=eT叩）心jQ（x）ef始Mdx+c3.贝努利方程 +P（x）y=Q（x）ya（a?t 0,1）dx令 z=y-a把原方程化为+（l-）P（x）z=（1 -a）Q（x）dx再按照一阶线性非齐次方程求解。dy 14.dx Q（y）-P（y）xdx可 化 为 卷+P（）X=Q（）以y为自变量

34、，x为未知函数再按照一阶线性非齐次方程求解。四.全微分方程及其推广（数学一）1.全微分方程P（x,y）dx+Q（x,y）dy=0,满足 。=尸dx dy通解：M（X,y）=C,其中“（x,y）满足 du（x,y）=P（x,y）dx+Q（x,y）dy求 （x,y）的常用方法。第一种：凑全微分法P（x,y）dx+Q（x,y）dy=A=dux,y）把常见的一些二元函数的全微分公式要倒背如流，就很有帮助。%2+y2a（1）xdx-ydy=d-口；2 它也是变量可分离方程，通解公式y=CeTM,（c为任意常数）x-(2)xdx-ydy=dn-2Or-12考研数学知识点-高等数学(3)y d x+xd y

35、 =d y xy)；(4)yd X +X d y=d(Sn ry Y.x y+)由=一心+办立 *处-泌=尸心2 _打：x2-f&7xd y -y d x Uy口(7)_(_ _ _ _ _ _ _=)办y)d y第三种：不定积分法由 普=P（x,y）得OXy d x-xd y x l(9)=JUar c t an ；9X+y y a/c，xd y-y d x,y D(10),.=d ar c t an7；”(x,y)=J P(x,y)d x+C(y)对y求导，得 Q(x,y)=也=N j P(x,y)d x+C1(y),d y d y2一 必，=/i gx y .7-5 21一办一9_户 产

36、).1 2后二(:；2)xd x+y d y 1 1(13 )7-6 =d _ 门Q+y2y l 2/+y2H(14)xd x-y d y =1 1 二；(x2-y2)2-J 2 x2-y2 d(|5)xd x+y d y =/】a r c t a n(x?+y2)L；l +(7-x2-+-y02)-02求出C（y）积分后求出c（y）2.全微分方程的推广（约当因子法）设P（x,y）d x+Q（x,y）d y=0不是全微分方程。d Q d P不满足一=一d x d y但是存在R（x,y）使得 R(x,y)尸(x,y)d x+R(九,y)Q(x,y)办 =0 为全微分方程，_LJ.LJ,口 c a

37、 R Q a RP也即满足=cd x d y第二利I特殊路径积分法（因为积分与路径无关）则R（x,y）称为约当因子，按全微分方程解法仍可求出13考研数学知识点-高等数学R（x,y）P（x,y）dx+R（x,y）Q（x,y）dy=du（x,y）通解y）=C。这种情形，求约当因子是关键。特殊的高阶微分方程14考研数学知识点-高等数学一.可降阶的高阶微分方程方程类型解法及解的表达式通解y=J/M W+W“次y=f(x,y)令y =p ,则y=，原方程=f(x,p)-阶方程，设其解为 P =g(x,G)，即y =g(x,q),则原方程的通解为y =J g(x,G)&+Q。y=f(y,y)令y=，把 看

38、 作y的函数，则,_ d p _ d p d y _ d p _y d x d y d x d y把y ,y的表达式代入原方程，得如=/(J,p)-一阶方程，d y P设其解为p =g(y,C,),即士g(y,C),则原方程的通解为d x f yd，y 浮线性微分方程解的性质与结构我们讨论二阶线性微分方程解的性质与结构，其结论很容易地推广到更高阶的线性微分方程。二阶齐次线性方程y+q G)y =O (i)二阶非齐次线性方程y，+p(x +q(x)y =火力(2)1.若y(x),%G)为二阶齐次线性方程的两个特解，则它们的线性组合GM(X)+C2 y 2(G，为任意常数)仍为同方程的解，特别地，

39、当 口。)工加2(%)(力为常数),也即0 6)与必(无)线性无关时,则方程的通解为 y =C y (x)+C y (x)I I 2 22若必(X),为3为二阶非齐次线性方程的两个特解，则 月(%)-%(X)为对应的二阶齐次线性方程的一个特解。3若歹(X)为二阶非齐次线性方程的一个特解，而y(x)为对应的二阶齐次线性方程的任意特解，则歹(x)+y(x)为此二阶非齐次线性方程的一个特解。4若歹为二阶非齐次线性方程的一个特解，而GM(x)+(x)为对应的二阶齐次线性方程的通解(G，为独立的任意常数)则y =式犬)+C,必(x)+G)是此二阶非齐次线性方程的通解。5设y(x)与(x)分别是y，+p(

40、x)V+q(x)y=f i(x)与y+p(x)y +q(x)y=/2(x)的特解，则M (x)+%(x)是y，+P(+虱=f +八 的特解。三.二 阶和某些高阶常系数齐次线性方程1.二阶常系数齐次线性方程y +p y +qy =O其 中p,q 为常数,特征方程/1 2 +p/l +q =0特征方程根的三种不同情形对应方程通解的三种形式(1)当 =p 2 4 q 0,特征方程有两个不同的实根4，15考研数学知识点-高等数学则方程的通解为y =Ge +C2e x(2)当 =?4q =0,特征方程有二重根4=4则方程的通解为y =(G +。2众.(3)当 =p 2 4 q ()+4 y (-D +A

41、 y(2)+A +p,i y +p“y =0其中夕收=1,2人，)为常数。相应的特征方程V +p V-+p/ln-2+A+p 2 +p =0I 2 n-n特征根与方程通解的关系同二阶情形很类似。(1)若特征方程有八个不同的实根4/U,A，A,则方程通解 y =C eA,x+C/+A +C eAxI 2 n(2)若4为特征方程的左 重实根0 w )则方程通解中含有(q+C 2 x+A +Ckxk-)e(3 )若a /为特征方程的左重共轨复根(2k x+A +D x*_|)s i n .由此可见，常系数齐次线性方程的通解完全被其特征方程的根所决定，但是三次及三次以上代数方程的根不一定容易求得，因此

42、只能讨论某些容易求特征方程的根所对应的高阶常系数齐次线性方程的通解。四.二阶常系数非齐次线性方程方程：+p y +qy =f(x)其中p,夕为常数通解：y=y+GM()+c 2 y 2。)其中G y (x)+C2%(x)为对应二阶常系数齐次线性方程的通解上面已经讨论。所以关键要讨论二阶常系数非齐次线性方程的一个特解如何求？我们根据/G)的形式，先确定特解 的形式，其中包含一些待定的系数，然后代入方程确定这些系数就得到特解y，一常见的/(X)的形式和相对应地y的形式如下：1./(x)=P(x),其中乙(X)为次多项式(1 )若0不是特征根，则 令y =R (x)=aox+a+A +a,x+a其中

43、6。=0,2人，)为待定系数。(2)若0是特征方程的单根，则令y=xR“(x)(3)若0是特征方程的重根，则 令 =2./侨=丹6卜其中勺(x)为次多项式，为实常数若不是特征根，则令=%)产(2)若 是特征方程单根，则令y=x R“(x),、(3)若 是特征方程的重根，则令y =(上.n3 ./(x)=Pn s in p x 或f x)=Pn(x)eaX co s x其 中 匕(x)为次多项式，皆为实常数(1 )若ai(3不 是 特 征 根，则 令y =eaX(x)co s /3x+Tn(x)s in (3x其中 R (x)=佝乂+a 广 +A +a,x+an4(i=0,A,)为待定系数T(x

44、)=b xl+b xnl+A +b x-hn 0 1 w-1 n(i =0,l,A,)为待定系数考研数学知识点-高等数学(2)若 是 特 征 根，则令y =xe R (X)COS(3T(x)sin/3x3.数量积。a-b=|a|fe|-cosa h+02b2+a3b3五.欧 拉 方 程（数学一）f y（）+p 短 尸+A+p W+P 卜=0,IM-1 n其 中p j（i=1,2,A,）为常数称为”阶欧拉方程。令x=e 代入方程，变为r是自变量，y是未知函数的微分方程，一定是常系数齐次线性微分方程。注意下面变换公式：d y _ d y d t _,d y _ 1 d y d y _ d y苏 济

45、 clx d t M 市 x x 力，d2y _d t d Q d y a/口 力口-2ld2y _2td y-2-=Qn=一Ge 一J=e-e d x d xd t n d xQ 力 口 d t n d t2 d t_ 1 d2y d y户产d t-口 c 口其中“人为向量a,匕间夹角 a b为数量也称点乘。a /表 示 向 量a在向量b上的投影，即a-bf=Pr j g4.向量积a x也称为叉乘。门口呻 怦*,卢 a x h的方向按右手法则垂直于a,b所在平面，且i j ka x b=aA a2 a3仇b2 b炉也=0 d x2 d t2向量代数与空间解析几何三.向量的运算a=ai-a2j

46、+a3k=%,a2 M3b=b+b?j+b3k=也 也 也 a x h是向量，a x h =-h x a o|Q X上等 于 以a,b 为邻边的平行四边形的面积。5.混合积：定义（ax/?）c,坐标公式%a2 a3（a,b,c）=仄 b2 byc=C|Z +c2j+c3/:=C19C2,C3几何意义|（。力4 j表 示 以 为 棱 的 平 行 大 面 体的体积。四.两向量间的关系设Q =为“，/=4也 也 1.加法。a+h =a+4,%+%，。3 +“3减法。a-h =a-b,a2 _打，/_ /2,数乘。2a=,然2,加3（4是常数）向量的加、减和数乘运算统称线性运算。关系向量表示向量坐标表

47、示a,b间夹角（0）a bC0SQ 3c。吟地+她+她1 1 2 3 1 1 2 3a与b垂直a-b=0aihl+a2b2+b3b3=017考研数学知识点-高等数学。与b平行a x b=0a a2%“b2 b3二.平面及其方程1.法（线）向量，法（线）方向数。与平面 垂直的非零向量，称为平面 的法向量，通常记成。法向量?,/?的坐标称为法（线）方向数。对 于 给 定 的 平 面，它的法向量有无穷多个，但它所指的方向只有两个。2.点法式方程 已知平面 过M（Xo，y（）,Zo）点，其法向量=A,8,C ,则 平 面 的 方 程 为（）（）（）A x-x0+B y-y0+C z-z0=0或 （r-

48、r0）=0其 中 为=%，M），Zo，r=x,y，z3.一般式方程Ax+By Cz+D=0其 中A,8,C不全为零。无y,z前的系数表示 的法线方向数，=A,B,C是 的 法 向 量。特别情形：Ax+B y+C z=O,表示通过原点的平面。Ax+By+D Q,平行于z轴的平面。A x+）=0,平 行yO z平面的平面。x=0表 示yO z平面。4.三点式方程设 A（x,y,z）,B（x,y ,z ）,C（x,y,z）三1 1 I 2 2 2 3 3 3点不在一条直线上，则 通 过A,8,C的平面方程为X-X|y-M Z-Z|尤2-2%-y Z2-z广 二o七一天 3-1 Z3-Z|设直线 L

49、的一般式方程为*幺 霜 猪5&处 丑!1 则 通 过L的所有平面方程 2 2 2 2为k A x+B y+C z +D）+k A x +B y +C z+D）=0I I 1 1 1 2 2 2 2 2,其中（A/）/（0,0）。6.有关平面的问题两平面为 :A x+8 y+G z+A =0乃2：+C2z+2=0%1与万2间夹角（9）COS0j A：+B：+q z 消；+B；+c：垂直条件A A，2+B B?+G。2=0平行条件为 B2 C2 2口重合条件2 A2 B?G D?设 平 面 的 方 程 为Ax+3y+Cz+O=0,而点为平面 外的一点，则M到平面 的距离d：Ax1+如 +CZj+D

50、VA2+B2+C2三.直线及其方程1.方向向量、方向数与直线平行的非零向量S,称为直线L的方向向量，方向向量的坐标称为方向数。2.直线的标准方程（对称式方程）。尤/_ y y）_ z zol m n其中（Xo，yo，zo）为直线上的点，/,加,为直线的方向数。3.参数式方程5.平面束18考研数学知识点-高等数学X XQ+I tA y =x+J”：z=z0 +n ts =/,/为参变量。4 .两点式设A（x,y,z）,B（x,y,z）为不同的两点，则1 1 I 2 2 2通 过A和B的直线方程为x-xL=y-yL=_ 2-Z j_电一修 必 一%Z 2-Z 5 .一般式 方 程（作为两平面的交线

51、）：*A X+5 y+G z +Q=OA x +3 y +C z+）=O ,方 向 向 量V 2 2 2 2S =A,B,C x A,B,C 1 1 I 2 2 26.有关直线的问题两直线为L .X _ X|_ y _M _z-Z|Z1 机 Ix -占 _ y 必 _ z z?2/2 恤 n24与4间夹角 cos e#+外吗+yllz+m-+n -r+m+n V 1 1 1 V 2 2 2垂直条件/|/2+mxm2+nxn2=0平行条件m _ n_/2 m2%平面的方程为:Ax+B y +Cz+D -0直 线L的方程为：X 7（）=y_%_ Z _ Z oI m nL与 间 夹 角().+Bm

52、+Cn_s ina =_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _J A?+B 2+C 2 d12+/+2L与垂直条件JL i n JiA二 B-CL与 平 行 条 件Al+B m+C鹿=0L与重合条件Al+B m +Cn=0上 有 一 点 在 上多元函数微分学多元函数的偏导数与全微分四.方向导数与梯度(数学一)1.平面情形z=(x,y)在 平 面 上 过 点K(Xo，y o)沿方向1=(co sa,c os p)的方向导数Af ./(0 +1 c os a,y0+t c os /3)-f xa,y 叼=lim_ _ _ _ _ _ _ _ _ _ _ _ _ _

53、 _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _a/、,%)7。tZ =f(x,y)在点Pu(x0,M)处的梯度为口/(%，%)凯/，%):g rad f(x0,y0)二-而方向导数与梯度的关系为 =g rad f(x0,y0-l。八无o，%=|g rad f a,%)c os l(g rad f(xa,y0),/)多元函数微分法复合函数微分法一一锁链公式模型 1.z=/(w,v),u=w(x,y),v=v(x,y)1 9考研数学知识点-高等数学d z=d z.d u+d z 一d vd x d u d x d v d xd z d z d u d z d v=-+

54、-d y d u d y d v d yz=z(x,y)（2）确定尤=x（y,z）则 史 二-刍 二 万 二 8d y F；d z F：（3）确定y =y（Z,X）则 改=-一 改=-可d z F；d x F；多元函数的极值和最值一.求z=f（x,y）的极值*x，y）=o第 一 步 （）求 出 驻 点v 八%y =o模型 3.u=f(x,y,z),y =y(x),z=z(x)在J+/-y (x)+r-z(x)d x x y 2模型 4.w=f(u,v),u=u(x,y,z),v=v(x,y,z).c r,Su r,d v d w _ f +f :治 海海%d w=f+f还有其它模型可以类似处理

55、区，九）（%=1,2,A ,/）第 二 步 令 k=/Ak，以）f Zk，然）-Z y U-%）若*（）则/（蒸，丸）不是极值若*=（）则不能确定（需从极值定义出发讨论）若*（）则/（符，以）是极值进 一 步 若 工：（川，以）0则/（，以）为极小值若 丁 一，九）0则/（%,%）为极大值二.求 多 元（2 2）函数条件极值的拉格朗日乘子法求 =/（%1 ,A ,X”）的极值*9 i（西，A，尤”）=0约束条件*M（m ）M（X 1,A ,X）=0作二.隐函数微分法F=F(占，八，x“,4,A,)=/(.r,A,%)+工人6(占,A,x)设 F(x,y,z)=0(1)确定 z =z(x,y)则

56、=-1产=-Fyd x F!d y F!20考研数学知识点-高等数学吊n=0X)f(x,y)d xV)AM*F 0n:或=9 i(X ,A，Z)=0*M.、f=(p(x,A,x )=0 ml n求 出(无 四,A ,x k=1,2,A ,/)是有可能的条件1 n极值点，一般再由实际问题的含义确定其充分性。这种方法的关键是解方程组的有关技巧。多元函数积分学二.在直角坐标系中化二重积分为累次积分以及交换积分顺序问题模 型/:设有界闭区域D=(x,y)a x b,(p、(x)y 仍3 其中夕i(x),0(x)在 a 上连续，在。上连续。则/(X，y b=J f(x,y)d xd y-(t)/(x,y

57、)d y G)模型：设有界闭区域。=(x,y)c y d,(y)x )在。上连续。关于二重积分的计算主要根据模型/或模型把二重积分化为累次积分从而进行计算，对于比较复杂的区域D,如果既不符合模型/中关于。的要求，又不符合模型 中关于D的要求，那么就需要把D分解成一些小区域，使得每一个小区域能够符合模型/或 模 型 中关于区域的要求，利用二重积分性质，把大区域上二重积分等于这些小区域上二重积分之和，而每个小区域上的二重积分则可以化为累次积分进行计算。在直角坐标系中，两种不同顺序的累次积分的互相转化是一种很重要的手段，具体做法是先把给定的累次积分反过来化为二重积分，求出它的积分区域D,然后根据D再

58、把二重积分化为另外一种顺序的累次积分。三.在极坐标系中化二重积分为累次积分在极坐标系中一般只考虑一种顺序的累次积分，也即先固定。对进行积分，然后再对。进行积分，由于区域。的不同类型，也有几种常用的模型。模型：设有界闭区域。=Q,q)a W e p,g)(0)y p(。)其中9 1(0)，*。)在 a，尸 上连续，/(/c o s ,/s i n 0);i。上连续，贝！|f x,y)d a=j j f(y co s8,y si n e)y d y d eD D=d e j c o s。,7 s i n 8卜d ya(p(e)模 型 /:设有界闭区域D=Q,q)O 64 2兀&(。)4 y 2(p

59、(。)则 J J/(x，y)d b=J J/(x，其中心(,夕2(。)在 上 连 续,21考研数学知识点-高等数学/(x,y)=/(y c o s O,y s i n。)在。上连续，则|J/(x,y)J c r =j j f(y co s8,y si n e)y d y d e=,(/c o s ,/s i n/9 y d yo :(e)模型：设有界闭区域D-(j,6a6/?,0 y4犬0 其中夕(。)在以用上连续，/(x,y)=/(y c o s a y s i n。)在。上连续，则f(x,y)d(y =j j f(/c o s 0,/s i n 0 y d y d 6-曲c o s 3,y

60、 s i n 0)y d y模 型 /：设有界闭区o=(%e)o v e w 2 ,o w”9(e)域f(x,y)=/(y c o s e,y s i n。)在。上连续，贝if(x,y)J c r=|j f(y co s。,y si n)y d y d ev=%a y)-f (乂)d b其 中。为闭曲面s在 孙 平面上投影区域z=/2(x,y)为上半曲面,z =(x,y)为下半曲面。2.空间曲面的面积其 中。为曲 面S在 孙 平面上投影，曲 面S的方程z =z(x,y)三重积分三重积分的计算方法1 .直角坐标系中三重积分化为累次积分(1)设。是空间的有界闭区域，Q =(x,y,z)z (x,y

61、)z z j x,y),(x,y)&D其 中。是 孙 平 面 上 的 有 界 闭 区 域，Z (x,y),Z 2(x,y)在。上连续,函数/(x,y,z)在。上连续,则J J J/a g z)小=J J 如M：；)/(尤，y-Mz(2)设C =(x,y,步夕z 0行;爱 四si段/舐/,y,z)cbcd y d z=JJJ/(psincos,psinsin(p,pcos)p2 snO dpd 0 d(pJQ,然后再根据。把三重积分化为关于p,9,（p的累次积分。曲线积分第一类曲线积分（对弧长的曲线积分）空间情形：空间一条逐段光滑曲线L上定义函数f（x,y,z）,把 曲 线L任 意 分 割 为

62、段，A St，A S2,A ,A S在上任取一 点（4，么,4）,如果对任意分割，任意取点，下列极限皆存在并且相等。1加 律,，$公）k2叫=1（这 里A S火又表示第氏段曲线的弧长，2 =m a x A S）以0则称此极限值为/（x,y,z）在曲线L上的第一类曲线积分，也称为对弧长的曲线积分，记以Jj（x，y,z/s如果曲线L是封闭曲线，也记以，/（x,y,z /S我们只讨论空间情形（平面情形类似）设空间曲线L的参数方程x=x（t）,y =y（t）,z-z（f）,（a?/?）则,（*，z）d S=7（4/）,y（t）,z（t 川 /（/）+3（讲 +上（/）小（假设/G，y,z）和 ），y（

63、r）,z ）皆连续）这样把曲线积分化为定积分来进行计算。二.第二类曲线积分（对坐标的曲线积分）空间情形：设空间一条逐段光滑有定向的曲线L=岫,函数尸（x,y,z）,Q（x,y,z）,R（x,y,z）在L上皆有定义，把L任 意 分 成 段，4a，1 ,A ,A S,在A SA.（1 Z:）上起点坐标为（X*T,yk_f,zk_）,终点坐标（按L的 定 向 决 定 起 点 和 终 点）令=xk xk-,A%=yk,AZA.=zk zk-9（k ）,y=y（f）,z =z（r）,起点A对 应 参 数 为，终点8对应参数为（注 意：现在 和 夕 的 大 小 不 一 定a#）如果P（x,y,z）,Q（x

64、,y,z）,R（x,y,z）皆连续，又 x （f）,y（t）,z G）也都连续，则+P（x,y,z）d x+Q（x,y,z）d y+R（x,y,z）d z=1凡电,削,2（派（/）+。削,削,z（/）y（/）+R 削，削这样把曲线积分化为定积分来计算。值得注意：如果曲线积分的定向相反，则第二类曲线积分的值差一个负号，而第一类曲线积分的值与定向无关，故曲线不考虑定向。三.两类曲线积分之间的关系i.平面情形设乙=岫平面上一个逐段光滑有定向的曲线，=4尸（，X z）cosa+Q（x,y,z）cos/3+R（x,y,z）cosy（Z sJA Bc其中c o s ，c o s /3,cos为曲线弧A3上

65、点（x,y,z）处沿定向A到8方向的切线的方向余弦。四.格林公式关于平面区域上的二重积分和它的边界曲线上的曲线积分之间的关系有一个十分重要的定理，它的结论就是格林公式。定 理1.（单连通区域情形）设孙平面上有界闭区域D由一条逐段光滑闭曲线L所围成的单连通区域。当 沿L正定向移动时区域。在L的左边，函 数P（x,y）,Q（x,y）在。上有连续的一阶偏导数，则有Ld Q d PQI f =混y =9+Q d y组 d e -d y 口 JL定理2.（多连通区域情形）设孙平面上有界闭区域。是（+1）连通区域（也即P（x,y），。（%,）在乙上连续,则有 个“洞”），它的边界L =C0Y C,Y A

66、Y C ,其中C oJ _ P（x,）灿 +Q（x,y）d y=j?（x,y）co sa+Q（x,y）c o s /3 d s%.J RB其中c o s ,c o s/7为曲线弧在点（x,y）处沿定向A到B方向的切线的方向余弦。2.空间情形设 乙=晶 为空间一条逐段光滑有定向的曲线，P（x,y,z）,Q（x,y,z）,H（x,y,z）在 L 上连续，则的定向为逆时针方向，G，A,c.定向皆为顺时针方向,仍符合沿L的正定向移动时区域。在它的左边这个原则。函数P（x,y）,0（x,y）在。上有连续的一阶偏导数,卜尸（司 y,z）dx+。（苍 y,z）dy+R（x,y,z）dzA B则24考研数学知识点-高等数学_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _值。如果对任意分割和任意取点，下列极限皆存在且相等n=f Pd x+Q d y+V f Pd x+Q d y五.平面上第二类曲线积分与路径无关的几个等价条件设尸 P（x,y）,Q（x,y）的分量