线性离散时间控制系统分析一.ppt

《线性离散时间控制系统分析一.ppt》由会员分享，可在线阅读，更多相关《线性离散时间控制系统分析一.ppt（67页珍藏版）》请在装配图网上搜索。

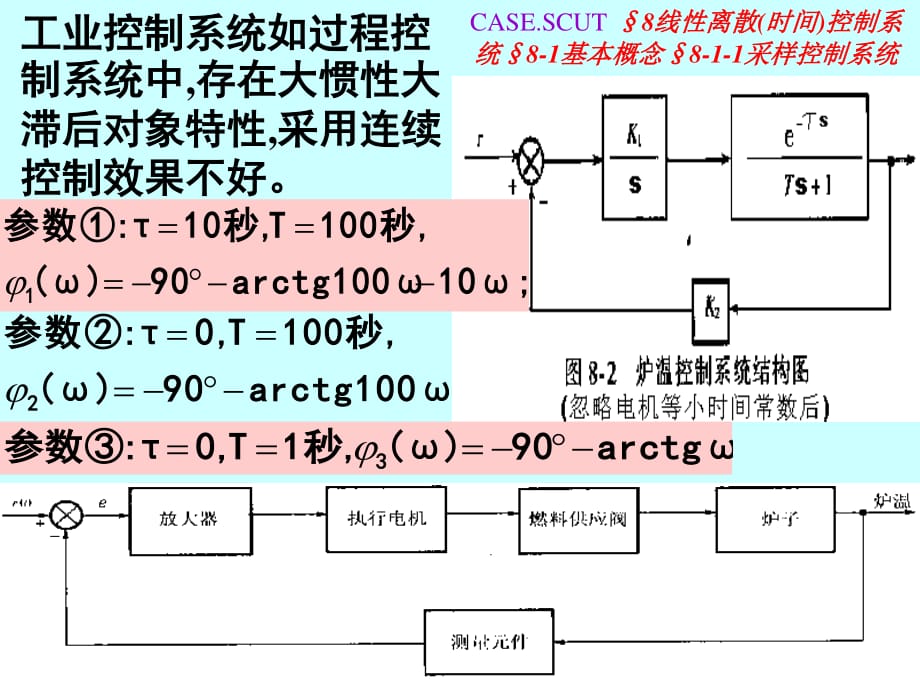
1、CASE.SCUT 8线性离散 (时间 )控制系 统 8-1基本概念 8-1-1采样控制系统 工业控制系统如过程控制系统中 ,存在大惯性大 滞后对象特性 ,采用连续 控制效果不好。 a r c t g 90( )1 秒,T0,:参数 3 1 0 ;a r c t g 1 0 0 90( ) 1 0 0 秒,T1 0 秒,:参数 1 arctg100 ;90( ) 1 0 0 秒,T0,:参数 2 CASE.SCUT 8-1基本概念 8-1-1采样控制系统 .稳态精度很差,很小, 只能K态品质, 要获得好的动 当T 、很大时, 0 故须用离散时间控制 30要获得,KKK 210 2.82.K :

2、参数系统 0.032;K :参数系统 0.018;K :参数系统 0 0 0 CASE.SCUT 8-1基本概念 8-1-1采样控制系统 CASE.SCUT 8-1基本概念 8-1-2数字控制系统 CASE.SCUT 2-6 脉冲传递函数 入的响应;系统对单位理想脉冲输 线性定常0 初始条件时,:脉冲传递函数 dttIS t t t )(; , , )( 00 0 s i n I s i n 2hdtr(t)eR ( j ) 的频谱函数 矩形脉冲 j t 脉冲序列的过程.把连续信号:采样过程 T.正比于采样瞬时值. 且 2 h )I脉冲序列的冲量( 面积 CASE.SCUT 8-2采样过 程和

3、采样定 理 8-2-1采 样过程和理 想脉冲序列 CASE.SCUT 8-2-1采样过程和理想脉冲序列 当充分短促的脉冲加在有惯性对象时 ,对象运动 仅取决于对象本身特性和脉冲冲量 ,而与脉冲具 体形状无关。 故采样控制系统的脉冲序列和数字 控制系统 A/D得的脉冲序列都处理为理想脉冲序 列 : 。( t ) 取代其它脉冲. 为此用I故可认为输出频谱相同 则输出c ( t ) 的频谱1 0 秒) 上,G ( s ) ( 设T 环节形脉冲分别作用到惯性冲量相同但不同的矩 .R ( j )G ( j )C ( j ),G ( j ) R ( j )C ( j ) 0.G ( j )但脉冲频谱虽不同

4、,而在惯性环节带宽外, ,脉冲的幅频谱均接近1不同但I 相同的几种带宽内, 在惯性环节而脉冲频带很宽,窄,由于惯性环节通频带很 CASE.SCUT 8-2-1采样过程 和理想脉冲序列 k skT s s2T s sT s k s s * s ss )ex ( k T )ex ( 2 T)ex ( Tx ( 0 ) )j k X ( s T 1 ( t ) L x s X s s k tjk sk sT T 2e T 1)kT( t(t) s s , )()( txsX L k tjk sk tjk s T 0k ssss ss * ss s x(t)e T 1 e T 1 x(t)(t)x(t

5、) )kT) ( tx(kT)2T) ( tx(2T )T) ( tx(Tx ( 0 ) ( t )(t)x n tj n s n tj n s T n s * s s s x ( t ) e T 1 e T 1 x ( t )( t )x ( t ) )nT( tx ( t )( t )x :0t0,设x ( t ):1 . 采样信号频谱 CASE.SCUT 8-2-2 采样 定理 )j k ( j X)jX ( j T 1 X ( j ) T 1 )jX ( j T 1 )j n X ( j T 1 ( j )X s * s ss s sn s s * 的二倍上限频率 大于或等于原信号 必

6、须2 / T 采样角频率复现, 不失真地把原信号 为:二. 采样定理 m a x ss n s s * )j n X ( s T 1( s )X( t ) xX ( s ) , x ( t ) 设 LL CASE.SCUT 8-2-2 采样 定理 X ( j )T1( j )XX ( j ) ,T1( j )X s * s * .2,1,n0,)jnX(jT1有时,2当 s s maxs 变成阶梯信号。 从而使采样信号到下一采样瞬时, 一直保持0 , 1 , 2 ,n), x ( n T 值( t ) 每采样瞬时采样使采样信号x,工程上常用零阶保持器 s * CASE.SCUT 8-2-3.

7、零 阶保持器 无畸变复现原信号.用一理想低通滤波器可 互不重迭.采样信号频谱中各波形采样定理满足时, SS s ss h 或 G ( j ) / )s i n ( / T ( j )G )e(1 s 1 ( s)G sT h s sT h se s 1 s 1 ( t ) g /2j T s s s /2j T/2j T/2j T j T h s sss s e /2T /2)s i n ( T T j )e(ee j e1 ( j )G CASE.SCUT 8-2-3. 零阶保 持器 )T1(t1(t)(t)g sh CASE.SCUT 8-3 Z变换 8-3-1采样 信号拉氏变换 8-3-

8、2 Z变换定义 k k s * )zx ( k TX ( z )( t ) x x ( t ) ZZ 且为超越函数。个零点,的周期函数. 有无穷多( s ) 为周期j X )ex ( k T)j k X ( s T 1 ( s )X( t ) x s * k skT s k s s * s 为此引入Z 变换。求解难,多个零极点, 有无穷也为s 的超越函数,)ex ( k TG ( s )( s )G ( s ) XC ( s ) k skT s * s zs * k k s lnz T 1 s * X ( s )X ( z ):X ( z ) . 注意( t ) x记( t ) 的Z 变换,X

9、 ( z ) 为x 称若级数收敛,)zx ( k TX ( z )(s)X s Z l n z . T 1则s,e引入z 平面复变量z s sT s 的一级数和式。 则可得Z 变换),瞬时值x ( k T求出x ( t ) 在各采样 z)x(kTX(z):1 . 级数求和法 s k k s CASE.SCUT 8-3-3 Z变换求法 ss s sss T1T t1T kk T22 T1Tt t ez z z)(e1 1 e则1,z)(e若 zezeze1e 0)(e2.x(t)例8 Z Z 1z z z1- 1 1(t)1,z若 为等比级数.,1z1z1z1z1(t) 0,1,2,k1,1(k

10、T)1(t),1.x(t)例8 -1 1 k210 Z Z z z z1 1z4.例8 1 0k kkk Z 2 s 1)(z zT1 ( t ) t Z )3z2zz(zT zkTz2TzTz01 ( t ) t 1 ( t )t3 . x ( t )例8 432 s k s 2 s 1 s 0 Z 21 1 321432 1)(z 1 ) 1z 1 ( dz d ) z1 z ( dz d )zz(z dz d 3z2zz CASE.SCUT 8-3-3 Z变换求法 n 1i Ts i n 1i i i si ez zA 则X ( z ) , ss A N(s) M(s) 设X ( s )

11、 :2 . 部分分式法 ss s s ss aTaT2 aT aT aT0T e)ze(1z )ez(1 ez z 1z z ez z ez z X(z) as 1 s 1 a)s(s a X(s) 5.例8 1)z( 2 c o s Tz z s i n T ez z 2j 1 ez z 2j 1 s i n t js 1/(2j) js 1/(2j) s s i n t 6.例8 s 2 s j Tj T 22 ss Z L CASE.SCUT 8-3-3 Z变换求法 CASE.SCUT 8-3-3 Z变换求法 2s1s 2)(s1)(s ss si sTsT Tsi 2 1i ez z

12、2)1 ) ( s(s 3)(s ez z 2)1 ) ( s(s 3)(s ez z )sX(ResX ( z ), 2)1 ) ( s(s 3s 7 . X ( s )-例8 ez z X ( s )s(s ds d 1)!(m 1 limX ( z ) s i i i sT m i1m 1m i1i l iss ez z)sR e s X (则X ( z ),为X ( s ) 的单重极点s设 n 1i Tsii si 则 的 X(s);s)(s ds d 1)!(m 1 lima:的留数为 处s则X ( s ) 在,s极点重个各为m. 设X ( s ) 含 i i i i m 1m 1m

13、 i ss 1 iii l 设X ( s ) 阶数为n .:3 . 留数计算法 CASE.SCUT 8-3-3 Z变换求法 8-3-4 Z变换 的基本定理 X(z)z)kTx(t:2 . 迟后定理 (z)Xa(z)Xa(t)xa(t)xa :四. 1 . 线性定理 k s 22112211 Z Z 2aT aT s assT2 )e(z ezT ez z a)(s 1 ds d 1 ) !(2 1 X ( z ) s s s 2 a)(s sss ss ss 3T2TT2 2TT 2TT e)ze(ez )2e(ezz ez z ez 2z X ( z ) 7.-续例8 a 为二重极点,sa)

14、(s 1X(s),te8.x(t)-例8 2at ; CASE.SCUT 8-3-4 Z变换的基本定理 ss s ss s 2aT s aT2 s aT aT s 2aT s aT at ec o s T2zez s i n Tze 1)ze( 2 c o s T)(ze s i n Tze s i n t e Z )X(zex(t)e:4 . 复位移定理 saTat Z 1z 1 1z z z)T 1 ( t9.例8 X ( z )z)kT x ( t:2 . 迟后定理 1 s k s Z Z )zx(mTX(z)z)kTx(t :3 . 超前定理 1k 0m m s k s Z 1)z(

15、2 c o s Tz z s i n T s i n t 1 0 .例8 s 2 s Z CASE.SCUT 8-3-4 Z变换的基本定理 1 0 . 2 0 80 . 4 1 61 0 . 7 9 2 0 . 2 0 80 . 4 1 6 zz 0 . 7 9 2 z lim 0 . 2 0 8 )0 . 4 1 6 z1 ) ( z(z 0 . 7 9 2 z 1 1 . 已知X ( z )例8 2 2 1z 2 2 1 ) X ( z )(zlim)x( 1z ) X ( z)z(1lim 1 ) X ( z)(zlim)x( 1 1z 1z X(z) z 1z lim x(t)lim)

16、x(kTlim 1z t s k X ( z)l i mx ( 0 ) z :5 . 初值定理 则单位圆外无极点,点,单位圆上无二重以上极 原点为圆心的设X ( z ) 在以z 平面:6 . 终值定理 CASE.SCUT 8-3-5 Z反变换 例 8-12 )4T1 5 0 ( t)3T7 0 ( t)2T3 0 ( t)T1 0 ( t(t)x 150,)x(4T70,)x(3T30,)x(2T10,)x(T0,x(0)可知: ssss * ssss 0.)x ( k T0 时,对应。设k可有无穷多个x ( t ) 故一X ( z )样瞬时的值,仅求得x ( t ) 在各采 X ( z )

17、,故通过 ,函数在各采样瞬时的值X ( z ) 仅含连续时间由于x ( t ) 的Z 变换 s 1 Z ).kT由其系数即可求得x (式,形式的无穷幂级数展开 整冪得到商为关于z),式M ( z ) 长除N ( z分母z 的多项式. 列直 ) 分别为分子式中M ( z ) 、N ( zM ( z ) / N ( z ) ,设X ( z ):1 . 长除法 s 1 4 s 3 s 2 s 1 s 0 4321 2 )zx ( 4 T)zx ( 3 T)zx ( 2 T)zx ( Tx ( 0 ) z 1 5 0 z7 0 z3 0 z1 0 z列直式长除得X ( z ) 23zz 1 0 z 2

18、)1 ) ( z(z 1 0 z 1 2 . X ( z )例8 X ( z) x ( k )x ( k T 1s Z:(t)求原采样函数x * 0 . 6 40 . 8 zz 0 . 1 4 3 )z ( z1 . 1 2 0 . 7 5z 1 . 5 zX ( z ) 2 查z 变换表再求和.后将其每项乘上z , 然分分式,X ( z ) / z 展开成部都有一个z 因子. 先将 一般Z 变换函数从变换表可看出,:2 . 部分分式法 0 , 1 , 2 ,k,21010 x ( k T ),2z1 0 z1z1 0 zX ( z ) k 2z 10 1z 10 2)1)(z(z 10 z

19、X(z), 2)1)(z(z 10z1 3 . X ( z )例8 0 . 6 40 . 8 zz 0 . 1 4 3 )1 . 1 2 ( z 0 . 7 5z 1 . 5 0 . 4 81 . 2 4 z1 . 5 5 zz 1 . 0 82 . 2 0 z2 . 6 2 z z X ( z ) 0 . 4 81 . 2 4 z1 . 5 5 zz 1 . 0 8 z2 . 2 0 z2 . 6 2 z 1 4 . X ( z )例8 223 2 23 23 CASE.SCUT 8-3-5 Z反变换 例 8-13 例 8-14 c/acos sin arctga r c c o s ,),

20、sin(ka sin 1 )(a) ( za(z c)z(z a2 a zz c)z(z k 22 11 ZZ CASE.SCUT 8-3-5 Z反变换 例 8-14续 )69.660sin(k(0.8) sin69.6 1.12 (0.75)1.5 (z)X(z)X)x(kT 69.6,60 0.5,0.8,0.64a0.143,c k k 21s 1 Z ( z )X( z )X0 . 6 40 . 8 zz 0 . 1 4 3 )1 . 1 2 z ( z0 . 7 5z 1 . 5 zX ( z ) 212 CASE.SCUT 8-3-5 Z反变换 3.留数法 R e s X ( z)

21、 z)x ( k T 1k s c 1k s c s c 1k dzX(z)z 2 j 1 )2 j x ( k T z dz )x(kTdzX(z)z 左侧。平面s( s ) 全部极点也在s则X 直线左侧,s 平面s若X ( s ) 全部极点在 1 * 1 为半径圆内.er对应z 平面原点为圆心 直线左侧s,eeeez 1s ssss T 1 jTTj )(TsT 1 s 3k s 2k s 1k k 0k s 1k1k )zx ( k T)zx ( 2 T )zx ( Tx ( 0 ) z z)x ( k TzX ( z ) z CASE.SCUT 8-3-5Z反变换 例 8-15,例 8

22、-16 1 单极点留数。) 等于z时，x ( k T2 , 3 ,k 1 俩单极点留数和；0 与z) 为zx ( T 1 单极点留数和；0 的二重极点和zx ( 0 ) 为z s s 0 , 1 , 2 ,k,21010 2)1 ) ( z(z 10z 2)1 ) ( z(z 10z 2)1 ) ( z(z 10z Res)x ( k T k k k s 2z 1z 1k 2)(z 1)(zz 2)1)(z(z 10z15.X(z)例8 1)z ( z e)ze(11 6 . X ( z )例8 /TT/TT ss R e s X ( z ) z)x ( k T 1k s 时不是极点。2 ，3

23、 ，1 时的单极点；kk 0 时的二重极点；0 为k的单极点。z1 始终是X ( z ) zz 1k CASE.SCUT 8-3-5 Z反变换 例 8-16 1k1-k zz 1)z(z e)ze(11 6 . X ( z )例8 /TT/TT ss 时不是极点。2 ，3 ，k 1 时的单极点；k 0 时的二重极点,0 为kz 的单极点;1 始终是X ( z ) zz 1k 1 1)z ( z e)ze(1 )x ( k T:2 , 3 ,k /TT/TT s ss 1z1)(z 0 1)(zz e)ze(1 1)(zz e)ze(1 dz d x ( 0 ) 2 /TT/TT 2 /TT/T

24、T ss ss 1z 0z 2 1)(z z /TT /TT/TT /TT/TT s s ss ss e1 1)z ( z e)ze(1 1)z ( z e)ze(1 )x ( T 1z 0z 1)(z z )2,3,1 ( 当k)x(kT,e1)x(T0,x(0) s/TTs s 1n 1k ssss n 0k )kT(nT T 1 s n 0k ssss kT1)T)g(nr(kT1)Tc(n e T 1 )r(kT)kT)g(nTr(kT)c(nT ss )g(0)r(nT1)T(ngnT1)Tr(n )2T)g(nTr(2T)T)g(nTr(T)r(0)g(nT ssss ssssss

25、s n 0k ssss )kT) g ( n Tr ( k T)c ( n T 0k ss * )kT) ( tr ( k T(t)r ;连续部分脉冲响应函数 设g ( t ) 为:一. 差分方程 t / T1 e T 1 1Ts 1g ( t ), 1Ts 11 7 . G ( s )例8 CASE.SCUT 8-4离散 (時間 )控制系統數學模型 kT1)T(n T 11n 0k s s ss e T 1 )r(kT 1)T1 7 续. c ( n例8 CASE.SCUT 8-4离散控制糸統的數學模型 例 8-17 1)r(ne(1c(n)e1)c(ne(12)c(n 1(t)e(1 1)

26、s(Ts 1 g(t), 1)s(Ts 1 G(s): 18 例8 /TT/TT/TT t/T sss 1L 1 ) Tr ( nT1)c ( n Te ss/TT s 1)Tr(n T 1 e T 1 )r(kTe 1)Tr(n T 1 e T 1 )r(kT s n 0k )kT(nT T 1 s /TT s n 0k kT1)T(n T 1 s ss s ss CASE.SCUT 8-4-1,2差分 方程和求解 例 8-19 0 , 1 , 2 ,n,2)(1)( C ( z ) Zc ( n ) nn1 分方程。分方程也为n 阶线性差 相应差则构成离散系统时,节, 线性环若系统连续部分

27、为n 阶 ).Z 反变换得c ( n T求解得C ( z ) ,为z 的代数方程, 化差分方程c(m)zC(z)zk)超前定理Z c ( n 先用:程二. Z 变換法解差分方 s 1k 0m mk 1c ( 1 )0,已知c ( 0 )0,2 c ( n )1)3 c ( n2)1 9 . c ( n例8 2z z 1z z 23zz z C(z):代入初始条件得 02C(z)zc(0)3zC(z)zc(1)c(0)zC(z)z 2 22 CASE.SCUT 8-4-1,2差分方 程和求解例 8-20 1 , 2 ,n,21c ( n ) 1n 0c(1)0,c(0)已知: 0n0, 0n1,

28、 u(n)2c(n) 1)3c(n2)20.c(n例8 无法查表. 但, 2z 1 1z 1 23zz 1 C(z) 12)C(z)3z(z:得Z 变换并代入初始条件 2 2 0 , 1 , 2 ,n,21 2z z 1z z z C ( z ) z c ( 0 ) z C ( z ) 1)c ( nz c ( 0 ) ,z C ( z )1 ) c ( n ,2 2z z ,1 1z z n11 11 n1n1 ZZ ZZZ ZZ (s)( s ) GR )jkG(s T 1 (s)R (s)RjkG(s T 1 * k s s * k * s s (s)G(s)R)er(kTG(s)C(s

29、) * 0k skT s s k s s * )j k R ( s T 1( t ) r( s )R k s * s s k s s * )j k (s)Rj k G ( s T 1 )j k C ( s T 1 ( t ) c( s )C R ( z ) G ( z ) ( s )G( s )R ( s )CC ( z ) l n z T 1 * l n z T 1 s * l n z T 1 s * ss s R(z) C(z)G(z) CASE.SCUT 8-4-3脉冲传递函数 1.定义 CASE.SCUT 8-4离散控制糸統的數學模型 8-4-3脉冲传递函数 1.定义 。只能得采样时刻

30、的信息 函数利用线性环节脉冲传递 传函) 。理想开关组合体的脉冲 节与脉冲传递函数( 线性环 称线性环节的函数的Z 变换, 脉冲响应G ( z ) 是线性环节的 R ( z ) G ( z ) , ( s )G( s )R ( s )CC ( z ) l n z T 1 * l n z T 1 s * l n z T 1 s * ss s 理想开关输入的Z 变换 线性环节输出的Z 变换 R ( z ) C ( z ) G ( z ) )()()()( * sGtgtgzG 1 LZZZ CASE.SCUT 8-4-3脉冲传递函数 2. 开环系统的脉冲传递函数 例 8-21,22,23 ss 2

31、T3T 2 ez z ez 2z G ( z ) 2s 1 3s 2 65ss 1s . G ( s ) 23 例8 G ( z )部分分式G ( s ) /TT s ez z T 1 G ( z ):查表 1 / Ts 1 / T 1Ts 1 . G ( s ) 21 例8 s10Tez z 1z z G(z) 10s 1 s 1 10)s(s 10 .G(s) 22 例8 CASE.SCUT 8-4-3脉冲传递函数 3. 环节串联时的脉冲传递函数 (z)GG ( s ) ( s ) GGG ( z ) :图( b ) 21 21 1 Z 脉冲传函乘积。 则总脉冲传函为各环节有理想开关分隔,

32、 若环节间几个环节串联, G ( z )( z )( z ) GG R ( z ) C ( z ) ( z ) R ( z )( z ) GG ( z ) D ( z )GC ( z ):图( a ) 12 12 2 CASE.SCUT 8-4-3脉冲传递函数 3. 环节串联时的脉冲传递函数例 8-24 s10T 1 ez z 1z z 10s 1 s 1 Z s1 0 T 21 ez 1 0 z 1z z ( z )( z ) GGG ( z ):( a ) 10s 10( s )G, s 1( s )2 4 . G例8 21 1 0 )s ( s 10 ( s ) ( s ) GG( z

33、)GGG ( z ):( b ) 1 21 1 21 Z Z ( z )G z 1z ( z )Gz( z )G )T(tg( t ) gG ( z ) 22 1 2 s22 ZZ CASE.SCUT 8-4-3 脉冲传递函数 4.有 零阶保持器的开环 系统 s ( s )G z 1z 01 Z (s)Ge(s)G(s)Ge(1(s)( s ) GG 2sT22sT21 ss ( s ) Ge( s ) G ( s ) Ge( s )G ( s ) ( s ) GG( z )GGG ( z ) 2 sT1 2 1 2 sT 2 1 21 1 21 s s ZZ Z Z ( s ) Ge)T(t

34、g( s ) ,G(t)g 2sT1s2212 s CASE.SCUT 8-4-3脉冲传递函数 4.有零阶保持器的开环系统例 8-25 0.3681.368zz 0.2640.368z ez z 1z z 1)(z z z 1z (z)G z 1z G(z) 2 T22 s s T2 s 2 22 0 2 s ez z 1z z 1)(z zT ( z )G 1s 1 s 1 s 1 1)(ss 1 s ( s )G ( s )G 1s2 5 . T例8 CASE.SCUT 8-4-3-5.离散控制系 统闭环脉冲传递函数例 8-26 0 . 0 0 7z 1 . 0 2 z 0 . 9 0 5

35、z 1 . 0 2 z ez 1 . 0 2 z ez 1 . 0 2 z G H ( z ) , 5s 1 . 0 2 0.1s 1 . 0 2 5s 5 0.1s 1 G ( s ) H ( s ) ss 5T0.1T E(z)GH(z)Y(z) E(z)G(z)C(z) Y(z)R(z)E(z) y(t)r(t)e(t) 0 . 9 0 5z z ez zG ( z ), 0.1s 12 6 . G ( s )例8 s0.1T (z) GH(z)1 G(z) R(z) C(z) G(s)H(s)GH(z) 1 Z CASE.SCUT 8-4-3-5.离散控制系 统闭环脉冲传递函数 例 8

36、-27 0 . 9 0 5z 0 . 9 5 ) 0 . 9 0 5z 1 0 z 1z 1 0 z ( z 1z G ( z ) ) 0 . 1s 10 s 10 )(e(1 0 . 1s 1 s e1 G ( s ) sT sT s s ( z ) ( z ) G H ( z )G1 ( z ) G ( z )G R ( z ) C ( z ) z)( z ) G H ( z ) E (GY ( z ) Y ( z )R ( z )E ( z ) )( z ) G ( z ) E ( zGC ( z ) c c c c ; 1z bz (z)G s b (s)G 27.例8 c c (z)

37、HGG1 (z)( z ) R GG(z)D ( z ) GC(z), (z)HGG1 (z)RG(z)D(z)DD(z) 12 12 2 12 1 21 (z)GH(z)G1 (z)G(z)G( z ) c c CASE.SCUT 8-4-3-5.离散控制系统闭环脉冲传递函数例 8-27,28 ; 0 . 0 0 7z 0 . 0 4 1 0 . 9 0 5z 2 . 0 4 1 z 1z 2z z 1z G H ( z ) ) 5s 0 . 0 4 1 0 . 1s 2 . 0 4 1 s 2 )(e(1 5s 1 0 . 1s 1 s e1 G ( s ) H ( s ) 2 7 续.例

38、8 sT sT s s (z)RG( s ) R ( s ) G(z)D( z ) ,HGGD ( z ) (z)例2 8 . D 1112121 Z CASE.SCUT 8-4-3脉冲传递函数表 8-2典型离散控制系统的结构图及输出 C(z) CASE.SCUT 8-4-3脉冲传递函数 表 8-2典型离散控制系统的结构图及输出 C(z) CASE.SCUT 8-4-3脉冲传递函数 表 8-2典型离散控制系统的结构图及输出 C(z) CASE.SCUT 8-4-3脉冲传递函数 表 8-2典型离散控制系统的结构图及输出 C(z) CASE.SCUT 8-4-4 差分方程与 脉冲传递函数 1.差分

39、方程与脉冲传递函数 关系 :均为离散控制糸统数学 模型 ,相互可转换。 例 8-20从例 8-17求得的差分 方程求脉冲传函 /TT /TT s s ez z T 1 R(z) C(z) G(z) zR(z) T 1 C(z)ezC(z) 1)r ( n T 1 c ( n )e1)c ( n 1Ts 1 G ( s ) /TT s CASE.SCUT 8-4-4差分方程与 脉冲传递函数 例 8-30从例 8-18求得的差分方程求脉冲传函 0 . 2 6 4 r ( n )1)0 . 3 6 8 r ( n 0 . 3 6 8 c ( n )1)1 . 3 6 8 c ( n2)c ( n /

40、TT/TT2 /TT /TT/TT/TT2 ss s sss e)ze(1z )ez(1 R ( z ) C ( z ) G ( z ) ) z R ( z )e(1C ( z )e) z C ( z )e(1C ( z )z 1) r ( ne(1c ( n )e1) c ( ne(12)c ( n 1)s ( T s 1 G ( s ) /TT/TT/TT sss 0.264)R(z)(0.368z0.368)C(z)1.368z(z 0.3681.368zz 0.2640.368z R(z) C(z) 31.G(z)例8 2 2 CASE.SCUT 8-4-4差分方程与 脉冲传递函数 不

41、会产生跳变。统输出信号在采样时刻 系阶保持器时,或连续环节前串联了零 0时sG(s)lim即时, 点比零点个数多2个当连续环节G ( s ) 极 s 行为；不符合实际物理系统的 1)Tr(n T 1 )c(nTe 1)Tc(n ez z T 1 G ( s ) ss /TT s/TT s s , 现象。 输出值产生不连续上,在离散时间n T 点个数不多于2 时,当G ( s ) 极点比零 s 系统的条件2 . 应用Z 变换法分析 0.1c ( 0 ):注意,1 . 5 5 3 z 1 . 5 0 3 z1 . 3 6 8 zz1 1z z ez z G ( z ) R ( z )C ( z )

42、 1sT1 s ,T1 ( t ) ,设r ( t ) , ez z T 1 G ( z ) :关组合体例一惯性环节与理想开 3 210 1 s /TT s )2T(t)T(tt1 )T(t* s2TsT* 0n s * ss s ss eee C ( s ) c ( t ) e 1s 1 1s 1 ( s )R 1s 1 C ( s ) ee1( t ) r( s )R )nT( t( t )另r CASE.SCUT 8-4-4差分方程与 脉冲传递函数 CASE.SCUT 8-5离散控制系 统稳定性分析 一 .离散控制系统稳定的充要条 件 :输出 C(z)的所有极点都位于 Z平面以原点为圆心

43、的单位圆内。 系统不稳定。重极点,若c ( z ) 有模为1 的 1R ( z )( t ) ,r ( t ) R ( z ) D ( z ) M ( z ) C ( z ) ll 1k n kks 1k k k pc)c ( n T, pz zc D ( z ) M ( z )C ( z ) 0 系统稳定;)c ( n Tl i m则1,p若 snk 系统不稳定;c(nT)lim则1,若C ( z ) 有一极点模 n 系统临界稳定;单极点,若C ( z ) 有模为1 的 CASE.SCUT 8-5离散 控制系统稳定性分析 圆内。Z 平面原点为圆心单位也即C ( z ) 极点位于 R(z) G

44、H(z)1 G(z) C(z) GH(z)1 G(z) R(z) C(z) ( z ) G H ( z )1 G ( z )C ( z ):1R ( z )( t ) ,设r ( t ) 左半s平面。(s)所有极点应位于C 0,)c(nTlimc(t)lim有 若系统稳定,C(z)(s)C * s nt ez * ssT 1,z则平面,( s ) 极点位于左半s即C0,若,ee eezj ,s *jTT j )(TsT ss ss CASE.SCUT 8-5离散系统 稳定性分析 离散控制系统稳定的充要条件为 :系统的特征方程 1+GH(z)=0的根都 在 z平面以原点为圆心的单位圆内。 1 1

45、w 1w z ,1w1w有 0,若R e w ,1w 1w令z:据二. R o u t h 稳定判 1;1w 1wz,1w1w有0,若R e w 1; 1w 1w z ,1w1w有 0,若R e w 039 1w 1w 1 1 9 1w 1w 1 1 7 1w 1w 45 , 1w 1w 令z0,391 1 9 z1 1 7 z4 5 z3 2 . D ( z )例8 23 23 CASE.SCUT 8-5离散控制 系统稳定性分析 例 8-32 w变换后 ,z平面以原点为圆心的单 位圆内部恰为左半 w平面 . Routh判据 :将 D(z)=1+GH(z)=0式 w变换为 p(w)=0式 ,列

46、写 Routh表 , 若 p(w)=0系数均为正数 ,且 Routh 表第一列元素均为正数 ,则 p(w)=0 所有根均位于左半 w平面 ,D(z)=0 所有根均位于 z平面以原点为圆心 的单位圆内 ,离散控制系统稳定。 。该离散控制系统不稳定0,aaa但不满足a0,其系数a 0402w2ww即p ( w ) 0321i 23 CASE.SCUT 8-5 离散控制系统稳定 性分析 例 8-33 1k0:03 . 8 )( 0 . 1 k)w0 . 2 k( 0 . 2w0 . 1 kp ( w ) 11121 0 . 9z zk 1z zk ez zk 1z zk( z )G 11 0 . 0

47、 1 T 11 1 s 00 . 9 )1 ) ( z(z 0 . 1 k1G ( z )1G H ( z )1 1 0 . 0 1s k s k 0 . 0 1 )s ( s 0 . 0 1 k ( s )G ( s )Ge 0 . 0 1 )s ( s e0 . 0 1 k 1)s ( 1 0 0 s ek G ( s ) 111 1 1 10s 10s 1 10s 1 0.9)1)(z(z 0.1k 0.9z zk 1z zkz(z)GzG(z) 1111 1 1 0)0 . 1 k( 0 . 91 . 9 zz0 . 1 k0 . 9 )1 ) ( z(zD ( z ) 121 CAS

48、E.SCUT 8-5离散控 制系统稳定 性分析 例 8-34 系统稳定.1,0 . 9 7 20 . 4 1 90 . 8 7 7z0 . 0 0 6 ,根模z 0,j 0 . 4 1 9 )0 . 8 7 7j 0 . 4 1 9 ) ( z0 . 8 7 70 . 0 0 6 ) ( z(z 0 . 0 0 60 . 9 5 4 z1 . 7 5 9 zz 22 2,31 23 0 . 0 0 7 )0 . 9 0 5 ) ( z(z 0 . 0 3 50 . 1 5 3 z 0 . 0 0 7z 0 . 0 4 1 0 . 9 0 5z 2 . 0 4 1 z 1z 2z z 1zG H

49、 ( z ) 0 导出0 . 0 0 7 )0 . 9 0 5 ) ( z(z 0 . 0 3 50 . 1 5 3 z1z z1( z ) G H ( z )G1由D ( z ) c )5s0 . 0 4 10 . 1s2 . 0 4 1s2)(e(15s 10 . 1s 1se1G ( s ) H ( s ) sT sT s s CASE.SCUT 8-5离散控制系统稳定性分析三 .Jury稳定判据 为实数.a0,a,zazazazaD ( z ) innn221100 CASE.SCUT 8-5离散控制系统稳定性分析三 .Jury稳定判据 为实数.a0,a,zazazazaD ( z )

50、 innn221100 CASE.SCUT 8-5离散控制系统稳定性分析 三 .Jury稳定判据 例 8-35 00 . 0 0 20 . 0 8 z0 . 4 z1 . 3 6 8 zzD ( z ) 234 0;2 . 6 9D ( z )1)(0;0 . 1 1 4D ( z ) 1z41z 0.512;c0.993c 0.083;b1b1;a0.002a 20 3040 系统稳定.均满足, 所有约束条件 CASE.SCUT 8-5离散控制系统稳定性分析 三 .Jury稳定判据 例 8-36 系统不稳定.2 在单位圆外,z0.5,z 00.5)2)(z(z 0.25)z2)(z(z法2

51、. D ( z ) 31,2 2 2 00 . 52 . 2 5 z3zzD ( z ) 23 系统不稳定.不满足稳定条件, 0,0.25法1 . D ( z ) 1z p1zp K1 极点时,z当G ( z ) 含一个以上G(z),lim1K式中, G(z)单位反馈时G H ( z ) , GH(z)1 R(z) 1)(zlim)e(nTlim)e( 1z s n CASE.SCUT 8-6离散 控制系统稳态误差分析 z ) 有关信号形式大小及GH( 差和输入一. 采样瞬时的稳态误 GH(z)1 R(z)(z)R(z)E(z), GH(z)1 1 R(z) E(z)(z) ee 差度二. 离

52、散控制系统的无 1z zrR ( z )1 ( t ) ,r1 . 阶跃输入r ( t ) 0 0 p 0 1z 00 1z 0 1z K r G(z)lim1 r G(z)1 zrlim G(z)1 1)z/(zr1)(zlim)e( CASE.SCUT 8-6离散控 制系统稳态 误差分析 例 8-38 态误差为0 。 使阶跃输入的稳 积分校正的引入, ( z ) G H ( z )G1 1 R ( z ) E ( z )( z )3 8 . 例8 c e 0 . 0 0 7 )0 . 9 0 5 ) ( z(z 0 . 0 3 50 . 1 5 3 zG H ( z ); 1z zR (

53、z )1 ( t ) ,r ( t ) 0, 0 . 0 0 7 )0 . 9 0 5 ) ( z(z 0 . 0 3 50 . 1 5 3 z 1)(z bz 1 z l i m ( z )zl i m 1z z ( z )1 ) (zl i m1 ) E ( z )(zl i m)e( 1z e 1z e 1z1z CASE.SCUT 8-6离散控制系统稳态误差分析 a 0 2 2 s 1z 0 32 s0 1z K a G ( z ) 1) ( z T 1 l i m a G ( z )1 1)1 ) / 2 ( zz ( zTa 1)(zl i m)e( vs1zv K1 极点时,z当

54、G ( z ) 含二个以上1 ) G ( z ) ,(zT1l i m式中K 2 s0 0 1)(z zTv R ( z ) 1 ( t )tv2 . 斜坡输入r ( t ) v 0 s 1z 0s0 1z 2 s0 1z K v 1 ) G ( z )(z T 1 lim v G ( z ) 1 ) 1(z Tv lim G ( z )1 1)z / ( zTv 1)(zlim)e( 3 s02 0 1)2(z 1)z(zTaR ( z )1 ( t ) ,ta 2 1)3 . 抛物线输入r ( t CASE.SCUT 8-6离散控制系统稳态 误差分析 1 极点个数.即为G ( z ) 含z

55、 G ( s ) 积分环节个数相同, 极点个数G ( z ) 与G ( s ) 的 .K时, 1 极点z当G ( z ) 含三个以上 a ).)e(,有关( T周期T 1 极点个数、采样含z z)误差与输入形式、G ( 系统稳态由上分析可知, ss CASE.SCUT 8-6离散控 制系统稳态 误差分析 例 8-37 CASE.SCUT 8-6离散控制 系统动态性能分析 )p(z 1z 1 D(z) M(z) lima pz za 1z z D(1) M(1) 1z z D(z) M(z) C(z) i pz i n 1i i i i 1)( z ) z / ( z( z ) R ( z )C

56、(z) 1)z/(zR(z)1(t),设r ( t ) 1,2,i1,pm . 设系统稳定，则n )p(s )z(s a b azaza bzbzb D(z) M(z) 设( z ) i n 1i i m 1j j n m 0 1n 1n n n 0 1m 1m m m 衰减愈快。 对应瞬态分量,，p 减，对应瞬态分量按指数衰 i 同.对应瞬态分量形式也不 在单位圆内位置不同,( t ) 的瞬态分量. p反变换为c 第二项( t ) 稳态分量;为c) / D ( 1 ) ,第一项反变换为M ( 1 pz za 1z z D ( 1 ) M ( 1 ) C ( z ) i * * n 1i i

57、i CASE.SCUT 8-6离散控制 系统动态性能分析 0)pl n ( T 1 式中： ea)p(a)( n Tc 为正实数p( 1 ) i s n T i n iisi i s 衰减越快越小,pn 为偶数时取正值) .( n 为奇数时取负值, 振荡过程瞬态分量是正负交替的,)p(a)( n Tc 为负实数p( 2 ) i n iisi i CASE.SCUT 8-6离散控制系统动态性能分析 振荡,衰减的振荡过程, ) 瞬态分量为c o s ( n pa2 epeaepea papa )( n Tc)( n Tc:相应瞬态分量 i ii n ii jnn i j i jnn i j i n 1i1i n ii s1isi iiii 的模和幅角. 1)D ( z ) ( z )pM ( z ) ( z 分别为和a也是共轭复数, ea对应系数a为一对共轭复数,epp(3) i ii pz i ii j i1ii, j ii CASE.SCUT 8-6离散控制系统动态性能分析 尤其不要靠近负实轴.左半圆, 布在靠近原点处. 而不要分 分分布在单位圆内右半部 可能脉冲传递函数极点应尽 闭环为使系统动态品质好, 减振荡。瞬态分量为正负交替衰2,k, 瞬态分量单调衰减；,k0,。振荡,k, 2 / 样周期数为k一个振荡周期包含的采 i ii i