线性代数第4章习题课

《线性代数第4章习题课》由会员分享，可在线阅读，更多相关《线性代数第4章习题课（11页珍藏版）》请在装配图网上搜索。

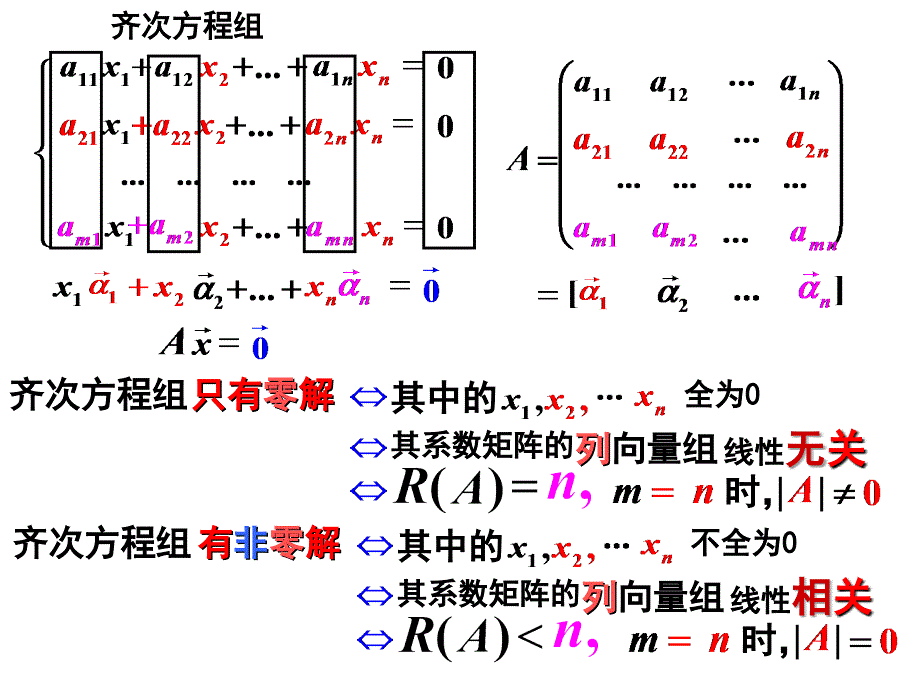
1、齐次方程组齐次方程组齐次方程组齐次方程组齐次方程组齐次方程组齐次方程组齐次方程组有有有有非非非非零零零零解解解解不全为不全为不全为不全为0 0 0 0其中的其中的其中的其中的其系数矩阵的其系数矩阵的其系数矩阵的其系数矩阵的列列列列向量组向量组向量组向量组线性线性线性线性相相关关时，时，时，时，齐次方程组齐次方程组齐次方程组齐次方程组只有只有只有只有零零零零解解解解全为全为全为全为0 0 0 0其中的其中的其中的其中的其系数矩阵的其系数矩阵的其系数矩阵的其系数矩阵的列列列列向量组向量组向量组向量组线性线性线性线性无无关关时，时，时，时，非齐次非齐次非齐次非齐次线性线性线性线性方程方程方程方程组组

2、组组 有解有解有解有解存在存在存在存在一组实数一组实数一组实数一组实数使使使使向量组向量组向量组向量组与向量组与向量组与向量组与向量组等价等价等价等价系数矩阵系数矩阵增广矩阵增广矩阵有唯一解有唯一解 有无穷多解有无穷多解无解无解 111111111111页（页（页（页（10101010）若若若若且三条且三条且三条且三条不同不同不同不同直线直线直线直线交于一点，交于一点，交于一点，交于一点，则矩阵则矩阵则矩阵则矩阵只有一个解只有一个解即即即即与与与与的秩满足的秩满足的秩满足的秩满足 课本课本课本课本112页页 2 2（3 3）设设设设是是是是矩阵矩阵矩阵矩阵,(A)(A)时时时时 非齐次线性方程

3、组非齐次线性方程组非齐次线性方程组非齐次线性方程组有解有解有解有解(B)(B)时时时时 非齐次线性方程组非齐次线性方程组非齐次线性方程组非齐次线性方程组有唯一解有唯一解有唯一解有唯一解(C)(C)时时时时 非齐次线性方程组非齐次线性方程组非齐次线性方程组非齐次线性方程组有解有解有解有解(D)(D)时时时时 非齐次线性方程组非齐次线性方程组非齐次线性方程组非齐次线性方程组有无穷多个解有无穷多个解有无穷多个解有无穷多个解选选选选（A A）时时时时(B)(B)错错错错例如例如例如例如无解无解无解无解(C)(C)错错错错例如例如例如例如无解无解无解无解(D)(D)错错错错例如例如例如例如无解无解无解无

4、解齐次线性方程组齐次线性方程组齐次线性方程组齐次线性方程组的通解的通解的通解的通解 若若若若则则则则的基础解系中的基础解系中的基础解系中的基础解系中个向量个向量个向量个向量有有有有其其其其通解通解通解通解为为为为 是任意常数是任意常数是任意常数是任意常数非齐次线性方程组非齐次线性方程组非齐次线性方程组非齐次线性方程组 解的性质解的性质解的性质解的性质的任何两个解的任何两个解的任何两个解的任何两个解则则则则是对应的是对应的是对应的是对应的齐次齐次齐次齐次线性线性线性线性方程组方程组方程组方程组则则则则非齐次线性方程组非齐次线性方程组非齐次线性方程组非齐次线性方程组的通解的通解的通解的通解的的的的

5、通解通解通解通解为为为为 的任何一个的任何一个的任何一个的任何一个特解特解特解特解的通解的通解的通解的通解115115115115页页页页13.13.13.13.设设设设 n n n n元元元元非齐次非齐次非齐次非齐次线性方程组线性方程组线性方程组线性方程组是它的是它的是它的是它的是对应的是对应的是对应的是对应的齐次齐次齐次齐次线性方程组线性方程组线性方程组线性方程组证明证明证明证明 ：（：（：（：（1 1 1 1）（2 2）的通解为的通解为的通解为的通解为证证证证 （1 1 1 1）的的的的基础解系基础解系基础解系基础解系根据条件根据条件根据条件根据条件的的的的nr nr nr nr 个个个

6、个解，解，解，解，根据根据根据根据线性线性线性线性无无无无关，关，关，关，线性线性线性线性无无无无关关关关,记记记记111111111111页页页页1 1 1 1（7 7 7 7）的一个的一个的一个的一个基础解系基础解系基础解系基础解系R(A)=r,R(A)=r,R(A)=r,R(A)=r,只有只有只有只有nr nr nr nr 个个个个 线性无关线性无关线性无关线性无关的解向量的解向量的解向量的解向量是是是是容易证明容易证明容易证明容易证明结论正确结论正确结论正确结论正确分析：分析：分析：分析：（2 2 2 2）的通解为的通解为的通解为的通解为其中其中其中其中通解通解通解通解11211211

7、2112页页页页2 2 2 2（8 8 8 8）选选选选(B(B)114114114114页页页页6 6 6 6通解通解通解通解个线性个线性个线性个线性无无无无关的解关的解关的解关的解114114114114页页页页7.7.7.7.设设设设三三三三元元元元非齐次非齐次非齐次非齐次线性方程组线性方程组线性方程组线性方程组满足满足满足满足所求的通解所求的通解所求的通解所求的通解的的的的基础解系基础解系基础解系基础解系中中中中是是是是Ax=0Ax=0的的的的2 2 2 2个个个个含有含有含有含有3-1=23-1=2个个个个线性无关的线性无关的线性无关的线性无关的解向量解向量解向量解向量线性无关的线性

8、无关的线性无关的线性无关的解向量解向量解向量解向量且它的三个解向量且它的三个解向量且它的三个解向量且它的三个解向量系数矩阵系数矩阵系数矩阵系数矩阵的的的的秩为秩为秩为秩为1 1，115115115115页页页页14141414 设设设设是是阶方阵阶方阵,51515151页页页页(10)(10)(10)(10)是是阶方阵阶方阵,则则53535353页页页页(10)(10)(10)(10)设设的伴随矩阵的伴随矩阵的秩的秩为为则则或或若若则则故故且且选选 或或或或或或或或或或或或且且 且且 设设 是是阶方阵阶方阵,115115页页页页9 9题题题题110110页例页例页例页例9 9是是阶非零方阵阶非

9、零方阵,求求及及设设设设是是阶方阵阶方阵,116116页页页页1515且且且且证明证明证明证明证证证证由由由由得到得到得到得到根据根据根据根据 110110页例页例页例页例9 9，得到得到得到得到根据根据根据根据88888888页页页页21212121得到得到得到得到故故故故 结论正确结论正确结论正确结论正确113113113113页页页页4 4 4 4（2 2 2 2）取何值时，取何值时，方程组方程组方程组方程组有有有有解解解解？解解解解求求求求其其其其通通通通解解解解，或或或或方程组有无穷多个方程组有无穷多个方程组有无穷多个方程组有无穷多个解解解解.通解为通解为通解为通解为通解为通解为通解为通解为