高等数学课件：1-5 函数的连续与间断

《高等数学课件：1-5 函数的连续与间断》由会员分享，可在线阅读，更多相关《高等数学课件：1-5 函数的连续与间断（54页珍藏版）》请在装配图网上搜索。

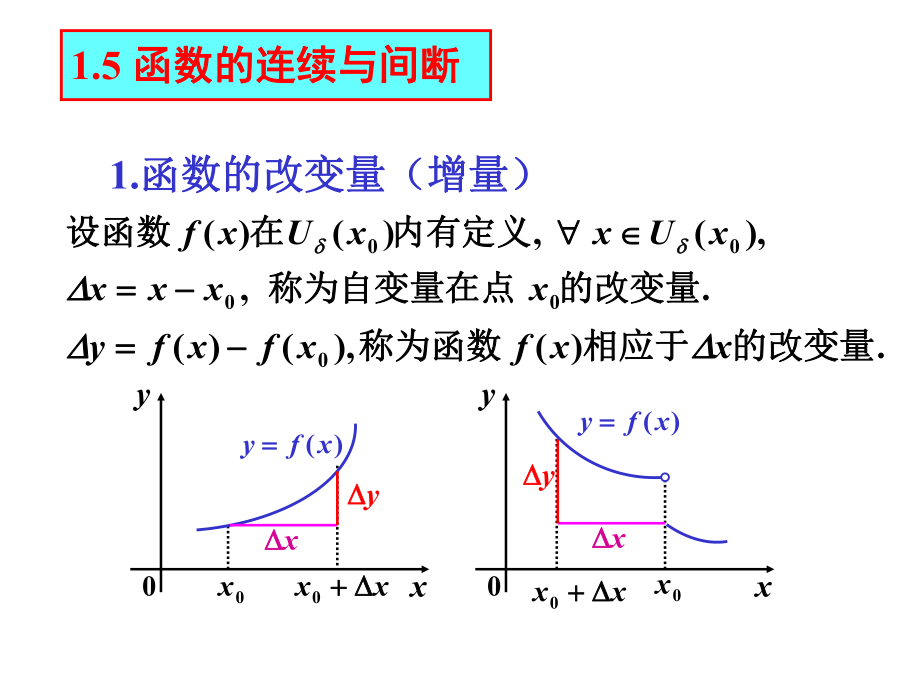
1、1.5 函数的连续与间断函数的连续与间断1.函数的改变量（增量）函数的改变量（增量）.,),(,)()(0000的改变量的改变量称为自变量在点称为自变量在点内有定义内有定义在在设函数设函数xxxxxUxxUxf .)(),()(0的改变量的改变量相应于相应于称为函数称为函数xxfxfxfy xy00 xxx 0)(xfy x y xy00 xxx 0 x y)(xfy 2.连续的定义连续的定义定定义义 1 1 设设函函数数)(xf在在)(0 xU 内内有有定定义义,如如果果当当自自变变量量的的改改变变量量x 趋趋向向于于零零时时,对对应应的的函函数数的的改改变变量量y 也也趋趋向向于于零零,即

2、即0lim0 yx 或或 0)()(lim000 xfxxfx,那那末末就就称称函函数数)(xf在在点点0 x连连续续,0 x称称为为)(xf的的连连续续点点.,0 xxx 设设),()(0 xfxfy ,00 xxx 就是就是).()(00 xfxfy 就是就是改变量式改变量式定义定义 1*1*设函数设函数)(xf在在)(0 xU 内有定义内有定义,如果如果函数函数)(xf当当0 xx 时的极限存在时的极限存在,且等于它在且等于它在点点0 x处的函数值处的函数值)(0 xf,即即 )()(lim00 xfxfxx 那末就称函数那末就称函数)(xf在点在点0 x连续连续.*1定定义义.)()(

3、,0,000 xfxfxx恒有恒有时时使当使当极限式极限式定定义义 ,)(0及其邻域有定义及其邻域有定义在点在点设函数设函数xxf.)(0处连续处连续在点在点则称则称xxf例例1 1.0,0,0,0,1sin)(处连续处连续在在试证函数试证函数 xxxxxxf证证,01sinlim0 xxx,0)0(f又又由定义由定义2知知.0)(处连续处连续在在函数函数 xxf),0()(lim0fxfx 3.单侧连续单侧连续;)(),()(lim,()(0000处处左左连连续续在在点点则则称称且且内内有有定定义义在在若若函函数数xxfxfxfxaxfxx .)(),()(lim,),)(0000处处右右连

4、连续续在在点点则则称称且且内内有有定定义义在在若若函函数数xxfxfxfbxxfxx .)()(,0,0000 xfxfxxx恒有恒有时时使当使当.)()(,0,0000 xfxfxxx恒有恒有时时使当使当定义定义 定义定义 ,)(0及其左邻域有定义及其左邻域有定义在点在点设函数设函数xxf.)(0处左连续处左连续在点在点则称则称xxf,)(0及其右邻域有定义及其右邻域有定义在点在点设函数设函数xxf.)(0处右连续处右连续在点在点则称则称xxf定理定理.)()(00处既左连续又右连续处既左连续又右连续在在是函数是函数处连续处连续在在函数函数xxfxxf)(lim)(lim)(lim(xfAx

5、fAxfaxaxax 根根据据)(lim)()(lim)()(lim(00000 xfxfxfxfxfxxxxxx 例例2 2.0,0,2,0,2)(连续性连续性处的处的在在讨论函数讨论函数 xxxxxxf解解)2(lim)(lim00 xxfxx2),0(f)2(lim)(lim00 xxfxx2 ),0(f 右连续但不左连续右连续但不左连续,.0)(处不连续处不连续在点在点故函数故函数 xxf)(xf：讨讨论论函函数数例例10,1 xex 0,0 x 0,sin xxx 处处的的连连续续性性。在在0 x,)(sinlim)(lim001 00 fxxxfxx处处不不连连续续。在在故故0 x

6、xf)(),(lim)(lim00 100fexfxxx 不右连续不右连续,解：解：处处左左连连续续；在在0 xxf)(例7：设 f(x)=考察在x=1处的连续性。1 ,11 1xx,x2)1(lim)(lim11 xxfxx例例7题解：题解：f(x)在在x=1处有定义，且处有定义，且f(1)=1。但是：。但是：处处间间断断。在在1)(1)1(2)(lim2)1(lim)(lim111 xxffxfxxfxxx注：可以重新定义：f(1)=2使得 f(x)在x=1时连续。所以x=1称为该函数的可去间断点。4.连续函数与连续区间连续函数与连续区间在区间上每一点都连续的函数在区间上每一点都连续的函数

7、,叫做在该区间上叫做在该区间上的的连续函数连续函数,或者说函数在该区间上连续或者说函数在该区间上连续.,)(,),(上连续上连续在闭区间在闭区间函数函数则称则称处左连续处左连续在右端点在右端点处右连续处右连续并且在左端点并且在左端点内连续内连续如果函数在开区间如果函数在开区间baxfbxaxba 连续函数的图形是一条连续而不间断的曲线连续函数的图形是一条连续而不间断的曲线.,:,连连续续即即，的的集集合合记记为为上上连连续续的的函函数数全全体体形形成成闭闭区区间间RbaffbaCbaCba oxy),(yxx ab)(xfy 例如例如,.),(内是连续的内是连续的有理函数在区间有理函数在区间则

8、有则有且且因为有理函数因为有理函数,0)(,)()()(0 xQxQxPxf)(lim)(lim)(lim000 xQxPxfxxxxxx)()(00 xQxP).(0 xf 例例如如：多多项项式式函函数数)()(lim00 xPxPxx 因为因为是连续的是连续的在在,),(01)(axaxaxPnn 例例3 3.),(sin内内连连续续在在区区间间函函数数证证明明 xy证证),(x任取任取xxxysin)sin()2cos(2sin2xxx ,1)2cos(xx.2sin2xy 则则,0,时时当当对任意的对任意的 ,sin 有有,2sin2xxy 故故.0,0 yx时时当当.),(sin都是

9、连续的都是连续的对任意对任意函数函数即即 xxy）上上连连续续。，在在（类类似似的的可可证证，xcos）上上连连续续。，在在（证证明明函函数数例例 xexf)(2).1ln()1ln(11 xex 0 xe),0(),1ln(),1ln(mineUx时时，则则取取处处连连续续。在在0)(0 xxf）上上也也连连续续。，在在（同同理理可可证证指指数数函函数数 xa.0处处连连续续在在证证明明：先先证证 xex,),10(,00 eex解不等式解不等式不妨设不妨设1lim00 eexx),1(),(0000 xxxxxeeeex,1limlim0000 uuxxxxxeexe处连续，处连续，在在由

10、由,lim00 xxxxee .0处处连连续续在在xex4、函数的间断点、函数的间断点:)(0条条件件处处连连续续必必须须满满足足的的三三个个在在点点函函数数xxf;)()1(0处处有有定定义义在在点点xxf;)(lim)2(0存在存在xfxx).()(lim)3(00 xfxfxx).()(),()(,00或或间间断断点点的的不不连连续续点点为为并并称称点点或或间间断断处处不不连连续续在在点点函函数数则则称称要要有有一一个个不不满满足足如如果果上上述述三三个个条条件件中中只只xfxxxf .振荡间断点振荡间断点无穷间断点；无穷间断点；第二类间断点第二类间断点跳跃间断点；跳跃间断点；可去间断点

11、；可去间断点；第一类间断点第一类间断点函数的间断点函数的间断点是第一类间断点是第一类间断点点点0 x 都存在都存在和右极限和右极限的左极限的左极限函数函数)()()(00 xfxfxf是第二类间断点是第二类间断点点点0 x 至少有一个不存在至少有一个不存在和右极限和右极限的左极限的左极限函数函数)()()(00 xfxfxf1.跳跃间断点跳跃间断点.)(),0()0(,)(0000的跳跃间断点的跳跃间断点为函数为函数则称点则称点但但存在存在右极限都右极限都处左处左在点在点如果如果xfxxfxfxxf 例例4 4.0,0,1,0,)(处的连续性处的连续性在在讨论函数讨论函数 xxxxxxf解解,

12、0)0(f,1)0(f),0()0(ff.0为函数的跳跃间断点为函数的跳跃间断点 xoxy2.可去间断点可去间断点.)()(),()(lim,)(00000的可去间断点的可去间断点为函数为函数义则称点义则称点处无定处无定在点在点或或但但处的极限存在处的极限存在在点在点如果如果xfxxxfxfAxfxxfxx 例例5 5.1,1,11,10,1,2)(处的连续性处的连续性在在讨论函数讨论函数 xxxxxxxfoxy112xy 1xy2 解解,1)1(f,2)1(f,2)1(f2)(lim1 xfx),1(f.1为为函函数数的的可可去去间间断断点点 x如例如例5中中,2)1(f令令.1,1,1,1

13、0,2)(处连续处连续在在则则 xxxxxxf跳跃间断点与可去间断点统称为第一类间断点跳跃间断点与可去间断点统称为第一类间断点.特点特点.,0但但是是函函数数不不连连续续处处的的左左、右右极极限限都都存存在在函函数数在在点点 xoxy112注意注意 可去间断点只要改变或者补充间断处函可去间断点只要改变或者补充间断处函数的定义数的定义,则可使其变为连续点，这种过程称则可使其变为连续点，这种过程称为对函数的连续延拓为对函数的连续延拓.,0,sin 是可去间断点是可去间断点点点例：函数例：函数 xxxy.0 .0 ,1;0,sin)(处连续处连续该函数在该函数在 xxxxxxf:补充定义后补充定义后

14、,sinlim1sinlimsinlim000 xxxxxxxxx 3.第二类间断点第二类间断点.)(,)(00的第二类间断点的第二类间断点为函数为函数则称点则称点在在右极限至少有一个不存右极限至少有一个不存处的左、处的左、在点在点如果如果xfxxxf例例6 6.0,0,0,1)(处的连续性处的连续性在在讨论函数讨论函数 xxxxxxf解解oxy,0)0(f,)0(f.1为函数的第二类间断点为函数的第二类间断点 x.断断点点这这种种情情况况称称为为无无穷穷间间例例7 7.01sin)(处的连续性处的连续性在在讨论函数讨论函数 xxxf解解xy1sin,0处没有定义处没有定义在在 x.1sinl

15、im0不存在不存在且且xx.0为第二类间断点为第二类间断点 x.断断点点这这种种情情况况称称为为的的振振荡荡间间注意注意 不要以为函数的间断点只是个别的几个点不要以为函数的间断点只是个别的几个点.,0,1)(是无理数时是无理数时当当是有理数时是有理数时当当xxxDy狄利克雷函数狄利克雷函数在定义域在定义域R内每一点处都间断内每一点处都间断,且都是第二类间且都是第二类间断点断点.,)(是无理数时是无理数时当当是有理数时是有理数时当当xxxxxf仅在仅在x=0处连续处连续,其余各点处处间断其余各点处处间断.o1x2x3xyx xfy ,1,1)(是无理数时是无理数时当当是有理数时是有理数时当当xx

16、xf在定义域在定义域 R内每一点处都间断内每一点处都间断,但其绝对值处但其绝对值处处连续处连续.判断下列间断点类型判断下列间断点类型:例例8 8.0,0,0,cos)(,处连续处连续在在函数函数取何值时取何值时当当 xxxaxxxfa解解xxfxxcoslim)(lim00 ,1)(lim)(lim00 xaxfxx ,a,)0(af),0()0()0(fff 要要使使,1时时故当且仅当故当且仅当 a.0)(处连续处连续在在函数函数 xxf,1 a小结小结1.函数在一点连续必须满足的三个条件函数在一点连续必须满足的三个条件;3.间断点的分类与判别间断点的分类与判别;2.区间上的连续函数区间上的

17、连续函数;第一类间断点第一类间断点:可去型可去型,跳跃型跳跃型.第二类间断点第二类间断点:无穷型无穷型,振荡型振荡型.间断点间断点(见下图见下图)可去型可去型第一类间断点第一类间断点oyx跳跃型跳跃型无穷型无穷型振荡型振荡型第二类间断点第二类间断点oyx0 xoyx0 xoyx0 x1.5.2连续函数的运算连续函数的运算定理定理1 1.)0)()()(),()(),()(,)(),(000处也连续处也连续在点在点则则处连续处连续在点在点若函数若函数xxgxgxfxgxfxgxfxxgxf 例如例如,),(cos,sin内内连连续续在在 xx.csc,sec,cot,tan在在其其定定义义域域内

18、内连连续续故故xxxx即：三角函数在其定义域上处处连续。即：三角函数在其定义域上处处连续。四则运算的连续性四则运算的连续性反函数与复合函数的连续性反函数与复合函数的连续性定理定理2 2 严格单调的连续函数必有严格单调的连严格单调的连续函数必有严格单调的连续反函数续反函数.例如例如,2,2sin上单调增加且连续上单调增加且连续在在 xy.1,1arcsin上也是单调增加且连续上也是单调增加且连续在在故故 xy;1,1arccos上单调减少且连续上单调减少且连续在在同理同理 xy.,cot,arctan上单调且连续上单调且连续在在 xarcyxy反三角函数在其定义域内皆连续反三角函数在其定义域内皆

19、连续.）上连续。）上连续。，在（在（）上连续，）上连续，在（在（0log xaax反三角函数、对数函数在其定义域上连续。反三角函数、对数函数在其定义域上连续。.)()(的图形相同的图形相同与其反函数与其反函数函数函数yxxfy 定理定理3 3).(lim)()(lim,)(,)(lim000 xfafxfaufaxxxxxxx 则有则有连续连续在点在点函数函数若若证证,)(连续连续在点在点auuf.)()(,0,0成立成立恒有恒有时时使当使当 afufau,)(lim0axxx 又又,0,0,00时时使当使当对于对于 xx.)(,)(,)(,)(00000也连续也连续在点在点则复合函数则复合函

20、数连续连续在点在点而函数而函数且且连续连续在点在点设函数设函数xxxfyuuufyuxxxxu 特别的，特别的，.)(成立成立恒有恒有 auax将上两步合起来将上两步合起来:,0,0,00时时使当使当 xx)()()()(afxfafuf .成立成立 )()(lim0afxfxx ).(lim0 xfxx 意义意义.)(.2的理论依据的理论依据变量代换变量代换xu 1.在函数连续时，极限符号在函数连续时，极限符号 可以可以与函数符号与函数符号 互换互换;lim0 xx f例例1 1.)1ln(lim0 xxx 求求.1)1(limln10 xxx eln 解解例如例如,),0()0,(1内连续

21、内连续在在 xu,),(sin内连续内连续在在 uy.),0()0,(1sin内连续内连续在在 xy连续，连续，连续，连续，xueexxfuxln,)(ln 在定义域上连续在定义域上连续 x)1ln(1lim0 xxx xxx)1ln(lim0 xxx10)1ln(lim 连续连续uyln,ln,)(ln连续连续连续，连续，axueeaxfuaxx .在定义域上连续在定义域上连续xa例例2 2.1lim0 xexx 求求.1)1ln(lim0yyy 原式原式解解,1yex 令令),1ln(yx 则则.0,0yx时时当当yyy10)1ln(1lim 同理可得同理可得xaxx1lim0 aalnl

22、n1 aaxeaxxlnln1limln0 xeaxx1limln0 xexax1limln0 0,1)1(lim0 axxax例：求例：求,0,0,1)1(时时当当解：令解：令xxa axxax )1ln(1lnlim0 1lim0 xx xxax1)1(lim0 ,11ln)1ln(xa ,1ln)1ln(xa ,1ln)1ln(,ax两边取对数两边取对数,1)1(ax 1)1(ax令令0,0 时时x,11)1(lim0 axxax)0(1)1(xaxxa初等函数的连续性初等函数的连续性三角函数及反三角函数在它们的定义域内是三角函数及反三角函数在它们的定义域内是连续的连续的.)1,0(aa

23、ayx指数函数指数函数;),(内单调且连续内单调且连续在在)1,0(log aaxya对数函数对数函数;),0(内单调且连续内单调且连续在在定理定理5 5 基本初等函数在定义域内是连续的基本初等函数在定义域内是连续的.xy ,),0(内连续内连续在在 ,不同值不同值讨论讨论(均在其定义域内连续均在其定义域内连续)定理定理6 6 一切初等函数在其一切初等函数在其定义区间定义区间内都是连内都是连 续的续的.定义区间是指包含在定义域内的区间定义区间是指包含在定义域内的区间.1.初等函数仅在其定义区间内连续初等函数仅在其定义区间内连续,在在其定义域内不一定连续其定义域内不一定连续;例如例如,1cos

24、xy,4,2,0:xD这些孤立点的邻域内没有定义这些孤立点的邻域内没有定义.,)1(32 xxy,1,0:xxD及及在在0点的邻域内没有定义点的邻域内没有定义.),1上连续上连续函数在区间函数在区间注意注意注意注意2.初等函数求极限的方法初等函数求极限的方法代入法代入法.例例3 3.1sinlim1 xxe求求1sin1 e原式原式.1sin e例例4 4.11lim20 xxx 求求解解解解)11()11)(11(lim2220 xxxxx原式原式11lim20 xxx20.0 所以所以连续连续因为函数因为函数,)(xf)lim()()(lim000 xfxfxfxxxx ”交换次序。”交换

25、次序。”可与符号“”可与符号“求极限时，极限号“求极限时，极限号“fxx0lim的的连连续续性性。讨讨论论函函数数例例 0,21010sin)(42xxexxxxxfx；是初等函数，处处连续是初等函数，处处连续）上，）上，解：在（解：在（xxxfsin)(0 续；续；也是初等函数，处处连也是初等函数，处处连）上，）上，在（在（xexfx21)(02 122lim21lim)(lim00200 xxxexfxxxxx处处，在在点点1sinlim)(lim00 xxxfxx),0(1)(lim0fxfx 在定义域上处处连续。在定义域上处处连续。)(xf.)(lim)(lim,)(lim,0)(li

26、m5)(lim00000BxvxxxvxxxxxxAxuxuBxvAxuxx ）（则则设设例例 )()(lim0 xvxxxu解解：.lnBAAeB ABeln )(ln)(lim0 xuxvxxe )(ln)(0limxuxvxxe )(0)(lnlimxvxuxxe )(lnlim)(lim00 xuxvxxxxe 的连续性的连续性根据指数函数根据指数函数te例例如如，1 exxxxxxsinlimsin100)sin1(lim xxxxxsinsin10)sin1(lim xxxxxsinsin10)sin1(lim xxx10)sin1(lim xxxxxx100coslimcosli

27、m 例：例：xxxxx1cos1cos101cos1lim xxxxx1cos1cos101cos1lim xxx101cos1lim .10 e的的连连续续性性。：讨讨论论例例nnnxxxf2211lim)(4时时，解解：当当1 x;111lim22 nnnxx时时，当当1 x;111lim22 nnnxx时时，当当1 x。011lim22 nnnxx)(xf 即即1,1 x 1,0 x 。1,1 x 1)(lim,1)(lim11 xfxfxx1)(lim,1)(lim11 xfxfxx续续。时时间间断断，在在其其他他地地方方连连在在1)(xxf连续函数的和差积商的连续性连续函数的和差积商

28、的连续性.复合函数的连续性复合函数的连续性.初等函数的连续性初等函数的连续性.定义区间与定义域的区别定义区间与定义域的区别;求极限的又一种方法求极限的又一种方法.两个定理两个定理;两点意义两点意义.反函数的连续性反函数的连续性.小结小结思考题思考题 若若)(xf在在0 x连连续续，则则|)(|xf、)(2xf在在0 x是是否否连连续续？又又若若|)(|xf、)(2xf在在0 x连连续续，)(xf在在0 x是是否否连连续续？思考题解答思考题解答)(xf在在0 x连续，连续，)()(lim00 xfxfxx)()()()(000 xfxfxfxf 且且)()(lim00 xfxfxx )(lim)

29、(lim)(lim0002xfxfxfxxxxxx)(02xf 故故|)(|xf、)(2xf在在0 x都连续都连续.但反之不成立但反之不成立.例例 0,10,1)(xxxf在在00 x不不连连续续但但|)(|xf、)(2xf在在00 x连连续续一、一、填空题：填空题：1 1、指出指出23122 xxxy 在在1 x是第是第_类间类间断点；在断点；在2 x是第是第_类间断点类间断点.2 2、指出指出)1(22 xxxxy在在0 x是第是第_类间类间断点；在断点；在1 x是第是第_类间断点；在类间断点；在1 x是第是第_类间断点类间断点.二、二、研究函数研究函数 1,11,)(xxxxf的连续性，

30、并画出函数的连续性，并画出函数 的图形的图形.练练 习习 题题三、三、指出下列函数在指定范围内的间断点，并说明这些指出下列函数在指定范围内的间断点，并说明这些间断点的类型，如果是可去间断点，则补充或改变间断点的类型，如果是可去间断点，则补充或改变函数的定义使它连续函数的定义使它连续.1 1、1,31,1)(xxxxxf在在Rx 上上 .2 2、xxxftan)(,在在Rx 上上 .四、四、讨论函数讨论函数 nnnxxxf2211lim)(的连续性，若有间断的连续性，若有间断点，判断其类型点，判断其类型.五、试确定五、试确定ba,的值的值,使使)1)()(xaxbexfx，（1 1）有无穷间断点

31、）有无穷间断点0 x；（2 2）有可去间断点）有可去间断点1 x.一、一、1 1、一类、一类,二类；二类；2 2、一类、一类,一类一类,二类二类.二、二、,),1()1,()(内连续内连续与与在在 xf1 x为跳跃间为跳跃间 断点断点.三、三、1 1、1 x为第一类间断点；为第一类间断点；2 2、,2为可去间断点为可去间断点 kx )0(kkx为第二类间断点为第二类间断点.0,12,tan)(1xkkxxxxf ),2,1,0(k,练习题答案练习题答案),2,1,0(2,02,tan)(2 kkxkkxxxxf.四、四、1,0,01,)(xxxxxxf1 x和和1 x为第一类间断点为第一类间断

32、点.五、五、(1)(1);1,0 ba (2)(2)eba ,1.一、一、填空题：填空题：1 1、43lim20 xxx_.2 2、xxx11lim0_.3 3、)2cos2ln(lim6xx _._.4 4、xxx24tancos22lim _.5 5、tett1lim2_.6 6、设、设,0,0,)(xxaxexfx 当当 a_时，时，)(xf在在 ),(上连续上连续.练练 习习 题题7 7、函数函数61)(24 xxxxxf的连续区间为的连续区间为 _._.8 8、设设 时时当当时时当当1,11,2cos)(xxxxxf确定确定 )(lim21xfx_;)(lim1xfx_._.二、二、

33、计算下列各极限：计算下列各极限：1 1、axaxax sinsinlim；2 2、xxxcot20)tan31(lim；3 3、1)1232(lim xxxx；三、三、设设 0),ln(0,10,)(22xxxbxxxaxf已知已知)(xf在在 0 x处连续，试确处连续，试确 定定a和和b的值的值.四、四、设函数设函数)(xf在在0 x处连续，且处连续，且0)0(f,已知已知)()(xfxg，试证函数，试证函数)(xg在在0 x处也连续处也连续.一、一、1 1、2 2；2 2、21；3 3、0 0；4 4、0 0；5 5、)11(212 e；6 6、1 1；7 7、),2(),2,3(),3,(；8 8、22,0,0,不存在不存在.二、二、1 1、acos；2 2、1 1；3 3；21e.三、三、eba ,1.练习题答案练习题答案