弦的横向振动解析ppt课件

《弦的横向振动解析ppt课件》由会员分享，可在线阅读，更多相关《弦的横向振动解析ppt课件（29页珍藏版）》请在装配图网上搜索。

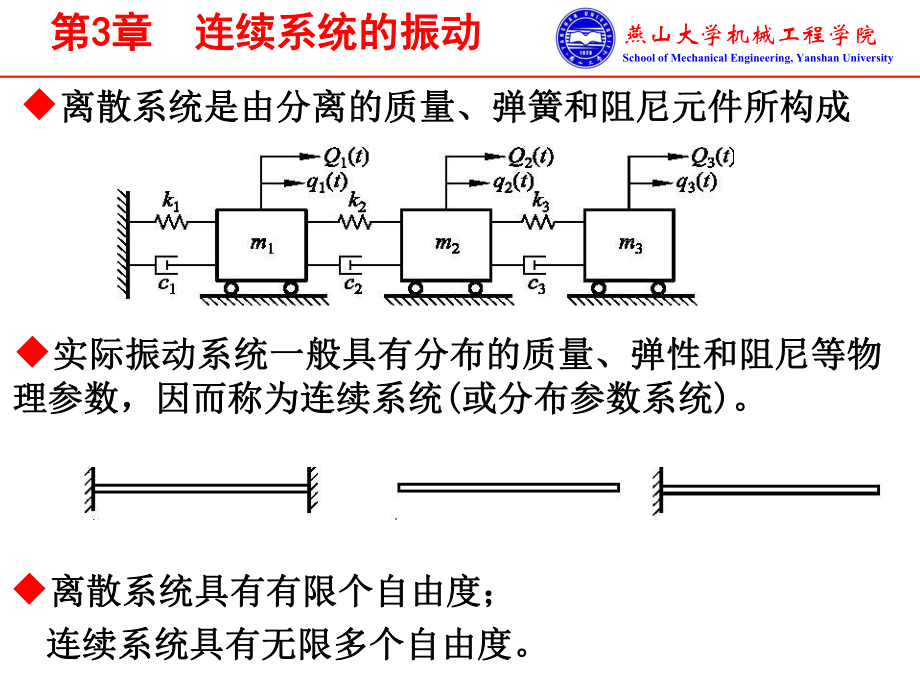
1、燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能离散系统是由分离的质量、弹簧和阻尼元件所构成离散系统是由分离的质量、弹簧和阻尼元件所构成第第3 3章章 连续系统的振动连续系统的振动离散系统具有有限个自由度；离散系统具有有限个自由度；连续系统具有无限多个自由度。连续系统具有无限多个自由度。实际振动系统一般具有分布的质量、弹性和阻尼等物实际振动系统一般具有分布的质量、弹性和阻尼等物理参数，因而称为连续系统理参数，因而

2、称为连续系统(或分布参数系统或分布参数系统)。燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能在数学上，离散系统的运动方程为方程数目与自由度在数学上，离散系统的运动方程为方程数目与自由度数目相等的二阶常微分方程组；数目相等的二阶常微分方程组；连续系统需要用时间和坐标的函数来描述它的运动状连续系统需要用时间和坐标的函数来描述它的运动状态，因此连续系统运动方程是偏微分方程。态，因此连续系统运动方程是偏微分方程。若把一

3、个连续系统离散为一个有限单元的集合，便成若把一个连续系统离散为一个有限单元的集合，便成了离散系统。反之，离散系统的极限情况就是连续系统。了离散系统。反之，离散系统的极限情况就是连续系统。离散系统是连续系统的近似描述，这也说明连续系统具离散系统是连续系统的近似描述，这也说明连续系统具有无限多的自由度。有无限多的自由度。燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能离散系统和连续系统具有相同的动力特性。连续系统的振

4、动理离散系统和连续系统具有相同的动力特性。连续系统的振动理论在概念方面严格地与离散系统相似；分析计算的过程也相似：论在概念方面严格地与离散系统相似；分析计算的过程也相似：(1)(1)建立系统运动微分方程建立系统运动微分方程 离散系统离散系统:常微分方程组常微分方程组;连续系统连续系统:偏微分方程组。偏微分方程组。(2)(2)求固有频率、振型、正则振型求固有频率、振型、正则振型离散系统离散系统:根据特征方程求固有频率、确定振型向量；根据正交性根据特征方程求固有频率、确定振型向量；根据正交性 确定正则振型向量。确定正则振型向量。连续系统连续系统:根据边界条件求固有频率、确定振型函数；根据正交性根据

5、边界条件求固有频率、确定振型函数；根据正交性 确定正则振型函数。确定正则振型函数。(3)(3)求正则坐标下的响应求正则坐标下的响应离散系统离散系统:正则坐标数为系统自由度数。正则坐标数为系统自由度数。连续系统连续系统:正则坐标数为无限个。正则坐标数为无限个。(4)(4)求原广义坐标下的响应求原广义坐标下的响应燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能连续系统的偏微分振动方程只在一些比较简单的特殊连续系统的偏

6、微分振动方程只在一些比较简单的特殊情况下才能求得解析解。例如均匀的弦、杆、轴和梁等情况下才能求得解析解。例如均匀的弦、杆、轴和梁等的振动问题。的振动问题。实际问题往往是复杂的，并不能归结为简单的连续系实际问题往往是复杂的，并不能归结为简单的连续系统情形，因而常常需要离散化成有限自由度系统进行计统情形，因而常常需要离散化成有限自由度系统进行计算或利用各种近似方法求解。算或利用各种近似方法求解。实际工程中常用的有限元法是将连续系统离散化的实实际工程中常用的有限元法是将连续系统离散化的实用有效方法之一。用有效方法之一。在研究连续系统的振动时，假设材料是均匀连续的和在研究连续系统的振动时，假设材料是均

7、匀连续的和各向同性的，并在弹性范围内服从虎克各向同性的，并在弹性范围内服从虎克(ook)ook)定理，定理，这些都是建立连续这些都是建立连续线性线性系统振动理论的前提。系统振动理论的前提。燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能简单的连续系统振动演示简单的连续系统振动演示燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近

8、平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能 设有一根细弦张紧设有一根细弦张紧于两固定点之间，弦长于两固定点之间，弦长为为L。两固定点连线方。两固定点连线方向取为向取为x x轴，与轴，与x x轴垂直轴垂直的方向取为的方向取为y y轴，如图轴，如图所示。所示。弦的单位长度质量为弦的单位长度质量为(x)，在横向分布力在横向分布力f(x,t)作用下作作用下作横向振动，张力为横向振动，张力为T(x,t)，跨长为，跨长为L，弦，弦x处的横向位移处的横向位移函数为函数为y=y(x,t)。3.1 3.1 弦的横向振动弦的横向振动燕山大学机械工程学院Scho

9、ol of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能 取微段弦线单元体取微段弦线单元体dx。假设弦作微小横向振动，假设弦作微小横向振动，则由牛顿定律得则由牛顿定律得 22d,ddsindsinyxfx txtTTxxTxx在微振动条件下，有在微振动条件下，有 xytansinxyTxxxyxyxTxxyxyTxt,xftyxddddd222222燕山大学机械工程学院School of Mechanical Engineering,Yanshan

10、 University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能式中式中xyTxxyxTxyT22xyTxxxyxyxTxxyxyTxt,xftyxddddd222222式中，不计式中，不计dx的二次项，的二次项，两边同时除两边同时除以以dx，整理，整理得得 xyxTxyTt,xfty2222燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能式中：

11、式中：=(x)，T=T(x,t)，y=y(x,t)。22,(0)yyTf x txLtxx弦的横向振动偏微分方程弦的横向振动偏微分方程弦横向振动的数学模型弦横向振动的数学模型弦横向振动的边界条件：两端处位移为零，即弦横向振动的边界条件：两端处位移为零，即 0,0tLyty上式为偏微分方程的边界值问题。上式为偏微分方程的边界值问题。22,(0)0,0yyTf x txLtxxyty L t燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发

12、挥中小学图书室育人功能假设：弦单位长度质量假设：弦单位长度质量(x)=常数；常数；弦内张力弦内张力T可视可视为常量；为常量；横向位移横向位移y(x,t)为小量为小量。如果如果f(x,t)=0，则弦的，则弦的自由振动微分方程为自由振动微分方程为 22222xyatyTa 弦横向振动数学模型简化为弦横向振动数学模型简化为 a表示弹性波沿弦向的传播速度。表示弹性波沿弦向的传播速度。上式通常称为上式通常称为波动方程。波动方程。2222,(0)0,0yyTf x txLtxyty L t 22,0,0yyTf x ttxxyty Lt 燕山大学机械工程学院School of Mechanical Eng

13、ineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能 连续系统的自由振动问题同离散系统的自由振动连续系统的自由振动问题同离散系统的自由振动问题在处理上可以用相同的方法；问题在处理上可以用相同的方法；观察弦的自由振动同样可以发现存在着同步运动观察弦的自由振动同样可以发现存在着同步运动的特征，即在运动中弦线位移的一般形状不随时间改变，的特征，即在运动中弦线位移的一般形状不随时间改变，但一般形状的幅度是随时间而改变的；但一般形状的幅度是随时间而改变的；运动中弦的各点同时到达最大幅值，又同时

14、通过平运动中弦的各点同时到达最大幅值，又同时通过平衡位置；衡位置；用数学的语言讲，描述弦振动的位移函数用数学的语言讲，描述弦振动的位移函数y(x,t)在在时间和空间上是分离的。时间和空间上是分离的。燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能上述边界值问题的解上述边界值问题的解可以写成下面的形式可以写成下面的形式 tFxYtxy,22222ddddFtYxYxaFttx Y(x)表示弦的振动位形，只表示弦的振

15、动位形，只取决于变量取决于变量x；F(t)表示弦的振动规律，只表示弦的振动规律，只取决于时间取决于时间t。22222xyaty将上式代入自由振动的波动方程将上式代入自由振动的波动方程 22222xyatyTa 22222dd1dd1xxYxYattFtF燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能 22222dd1dd1xxYxYattFtF左端只依赖于左端只依赖于t，右端只依赖于，右端只依赖于x，要使其对任

16、意的，要使其对任意的t和和x都都成立，必然等于同一常数。用成立，必然等于同一常数。用-2表示这个常数，得表示这个常数，得 222222dd1dd1xxYxYattFtF由该式得到如下由该式得到如下两个方程两个方程 0dd222tFttF 222d00dY xY xxLxa关于时间变量关于时间变量t的常微分方程。的常微分方程。关于空间变量关于空间变量x的常的常微分方程。微分方程。将偏微分方程转化为两个二阶常微将偏微分方程转化为两个二阶常微分方程！分方程！分离变量法。分离变量法。燕山大学机械工程学院School of Mechanical Engineering,Yanshan Universit

17、y为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能关于时间变量关于时间变量t的的常微分方程常微分方程 0dd222tFttF sincossinF tAtBtCt方程的通解为方程的通解为 式中：式中：A，B(或或C，)为积分常数。由两个初始条件为积分常数。由两个初始条件y(x,0)和和 来确定。来确定。0,xy 燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室

18、育人功能关于空间变量关于空间变量x的常微分方程的常微分方程 xExDxYcossin式中：式中：D，E为积分常数。由边界条件为积分常数。由边界条件y(0，t)和和y(L，t)来确定来确定。显然，显然，D=0不是振动解。不是振动解。上式通解为上式通解为0,sin0EDLsin0La弦振动的特征方程弦振动的特征方程 222d0,0dYxYxxLxa称为振型函数称为振型函数0sin0DL 00LYY ,0,=0,=0y x tY x F tyty Lt，燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国

19、特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能由特征方程，可求得无由特征方程，可求得无限多阶固有频率：限多阶固有频率：1,2,rrarTrLL第第1阶固阶固 频率频率 1称为基频，或基谐波；称为基频，或基谐波；高阶固有频率高阶固有频率 r(r=2，3，)称为高次谐波。称为高次谐波。高次谐波是基谐波的整数倍。高次谐波是基谐波的整数倍。对应于无限多阶固有频率，有无限多阶固有振型函数对应于无限多阶固有频率，有无限多阶固有振型函数 sincos1,2,rrrYxDxExr1,2,rrrraLE=0 因为振型只确定系统中各点振因为振型只确定系统中各点振动幅度的相对值

20、，其表达式无动幅度的相对值，其表达式无需带常数因子需带常数因子D，取，取D=1。sin1,2,rrY xxrL燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能离散系统的固有振型是以各质点之间的振幅比来表示离散系统的固有振型是以各质点之间的振幅比来表示的；的；当离散系统的质点数趋向于无穷时，各质点振幅就成当离散系统的质点数趋向于无穷时，各质点振幅就成为为x的连续函数，即为连续系统中的振型函数的连续函数，即为连续系统

21、中的振型函数Y(x)；离散系统所描绘的固有振型只是连续系统振型函数离散系统所描绘的固有振型只是连续系统振型函数Y(x)所表达的真实振型的近似解。所表达的真实振型的近似解。燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能弦的自由振动可以表示为各阶固有振动的叠加，即有弦的自由振动可以表示为各阶固有振动的叠加，即有 11,sincossinrrrrrrrrry x tYx F tAtBtxL对应于第对应于第r阶固有频率

22、，弦的固有振动为阶固有频率，弦的固有振动为 xLrtBtAtFxYtxyrrrrrrrsincossin,11,cossinsinrrrrrrrrrry x tF trYxAtBtxttL燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能弦自由振动对初始条件的响应弦自由振动对初始条件的响应设设t=0的初始条件为的初始条件为 ,0,0()y xy xf xg xt 1111,sincossin,cossinsinrr

23、rrrrrrrrrrrrrrrrry x tY x F tAtBtxLy x tF trY xAtBtxttL 11,0sin,0sinrrrrrry xBxfxLy xrAxg xtL燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能初始条件初始条件表示为表示为 11,0sin,0sinrrrrrry xBxfxLy xrAxgxtL由三角函数的由三角函数的正交性，有正交性，有 LsrLsrxLxsLxr 0 2

24、 0dsinsin 0 02sind1,2,1 2sindLrLrrr xBfxxLLrr xAg xxLL张紧弦的自由振动，除张紧弦的自由振动，除了基频振动外，还可以了基频振动外，还可以包含谐波振动。在振动包含谐波振动。在振动中各种谐波的出现与否中各种谐波的出现与否以及出现的相对大小取以及出现的相对大小取决于激励条件。决于激励条件。燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能例例1 如图所示的两端固定的弦。

25、求振如图所示的两端固定的弦。求振动的前三阶固有频动的前三阶固有频率和相应的固有振型，并作出振型图率和相应的固有振型，并作出振型图。11sinTYxxLL 2222sinTYxxLL 3333sinTYxxLL实例实例解：固有频率和振型函数为解：固有频率和振型函数为 1,2,rr arTrLL sin1,2,rrY xxrL燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能系统各阶固有频率值系统各阶固有频率值由低到高

26、成倍增长，相由低到高成倍增长，相应振型波形逐渐增多；应振型波形逐渐增多；振幅为零的点称为节振幅为零的点称为节点，节点数随阶次的增点，节点数随阶次的增加而逐一增加，第加而逐一增加，第n阶阶固有振型有固有振型有n-1个节点。个节点。燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能 0 2 0d,1,2,dddddLrsrsLrsrYx Yxxr sYxYrTxxx 例例-2 考虑均匀弦在考虑均匀弦在x=0和和x=L处

27、固定的特征值问题，证处固定的特征值问题，证明特征函数明特征函数Yr(x)和和Ys(x)满足正交性关系：满足正交性关系：式中式中 rs为克朗尼格符号。为克朗尼格符号。1(),1,2,0()rsrsr srs燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能把振型把振型 代入上式，得代入上式，得 sin1,2,rrr xY xDrL 222 0 02012sind1 cosd2sin 21122LLrrLrr xr x

28、DxDxLLr x LDxrL21,2,rDrL正则振型函数为正则振型函数为 2sin1,2,rrYxxrLL(1)(1)振型函数正则化振型函数正则化 2 0d11,2,LrYxxr解：解：燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能(2)(2)对分布质量的正交性对分布质量的正交性 0 0 002dsinsind1coscosdsin/sin/1/0 1 LLrsLLrsr xs xYx YxxxLLLrsx

29、rsxxLLLrsx Lrsx LLrsLrsLrsrs燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能 0 02ddddd2coscosd22,1,2,LrsLrsrsrsrsrrsYxYrTxxxrsr xs xTxL L LLLrsLTL L LT rT sLLr s (3)(3)对张力的正交性对张力的正交性 2sinrrYxxLL燕山大学机械工程学院School of Mechanical Enginee

30、ring,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能注意：注意：在本例中，在本例中，特征函数为特殊的三角函数。特征函数为特殊的三角函数。特征特征函数函数Yr(x)满足的正交关系式仅仅是普通三角函数正交满足的正交关系式仅仅是普通三角函数正交性的重复。然而，在本质上特征函数的正交性具有性的重复。然而，在本质上特征函数的正交性具有一般一般性性(即振型函数为一般函数时，也满足正交性条件即振型函数为一般函数时，也满足正交性条件)。根据所学过的离散系统振动理论，离散系统同样具有根据所学过的离散系统振动理

31、论，离散系统同样具有振型的正交性，同样有一组固有频率和固有振型来表示振型的正交性，同样有一组固有频率和固有振型来表示系统的特征。离散系统的固有频率和固有振型是有限集；系统的特征。离散系统的固有频率和固有振型是有限集；而连续系统的固有频率和固有振型是无限集。除此以外，而连续系统的固有频率和固有振型是无限集。除此以外，离散系统和连续系统的相似性是完备的。离散系统和连续系统的相似性是完备的。燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥

32、中小学图书室育人功能例例3 设张紧弦在初始时刻将中点拨至图示位置，然后设张紧弦在初始时刻将中点拨至图示位置，然后无初速地释放，求弦的自由振动。无初速地释放，求弦的自由振动。解：令解：令h表示弦在中点的位移，表示弦在中点的位移，初始条件是初始条件是 2 02,0,21 2,00hx LxLy xf xhx LLxLy xg xt故有故有 01 2sind01,2,Lrrr xAg xxrLL燕山大学机械工程学院School of Mechanical Engineering,Yanshan University为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能弦的自由振动可以表达为弦的自由振动可以表达为 tTLLxtTLLxtTLLxhtxy 5cos5sin251 3cos3sin91 cossin8,2设设r=2n+1，上式可以写成，上式可以写成 tTLnLxnnhtxynn 12cos12sin1218,022为奇数为偶数rrhrr 18 02122 2 0 2 0 dsin12dsin22dsin2LLLLrxLxrLxhxLxrLhxLxLxrxfLB