圆锥曲线讲义

《圆锥曲线讲义》由会员分享，可在线阅读，更多相关《圆锥曲线讲义（18页珍藏版）》请在装配图网上搜索。

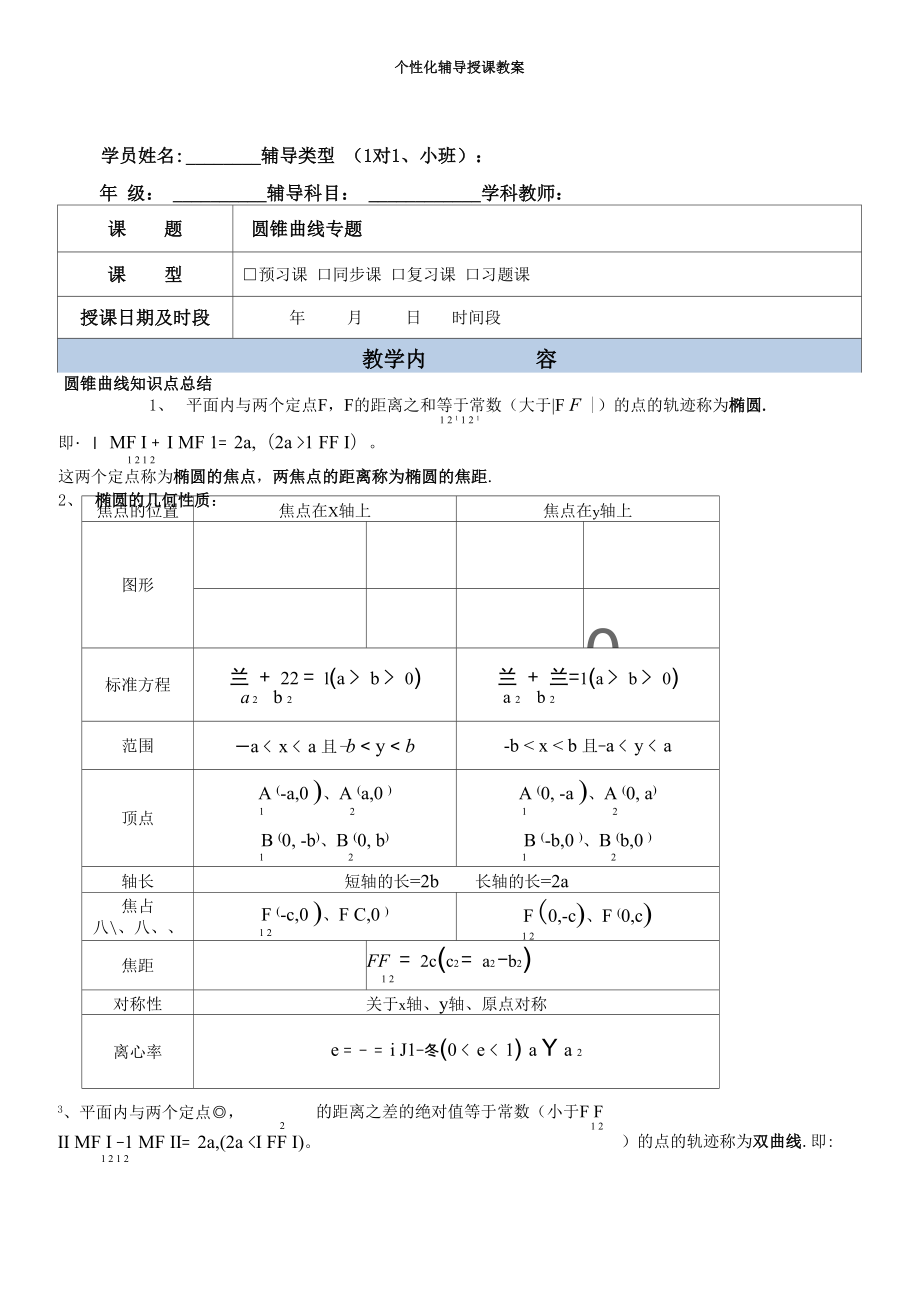
1、个性化辅导授课教案）的点的轨迹称为双曲线.即:学员姓名:辅导类型 （1对1、小班）：年 级：辅导科目：学科教师：课题圆锥曲线专题课型预习课 口同步课 口复习课 口习题课授课日期及时段年月日时间段教学内容圆锥曲线知识点总结1、平面内与两个定点F，F的距离之和等于常数（大于|F F |）的点的轨迹称为椭圆.1 2 1 1 2 1焦点的位置焦点在X轴上焦点在y轴上图形0，标准方程兰 + 22 = l(a b 0)a 2b 2兰 + 兰=1(a b 0)a 2b 2范围一a x a 且-b y b-b x b 且-a y a顶点A (-a,0 )、A (a,0 )12B (0, -b)、B (0, b

2、)12A (0, -a )、A (0, a)12B (-b,0 )、B (b,0 )12轴长短轴的长=2b长轴的长=2a焦占八、八、F (-c,0 )、F C,0 )1 2F(0,-c)、F (0,c)1 2焦距FF = 2c(c2 = a2 -b2)1 2对称性关于x轴、y轴、原点对称离心率e = - = i J1-冬(0 e 1 FF I）。1 2 1 2这两个定点称为椭圆的焦点，两焦点的距离称为椭圆的焦距.2、椭圆的几何性质：3、平面内与两个定点，2的距离之差的绝对值等于常数（小于F F1 2II MF I -1 MF II= 2a,(2a 0,b 0)a 2b 2y2 - X2 = 1

3、(a 0, b 0) a 2b 2范围x a , y e Ry a , x e R顶点A (-a,0 )、A (a,0 )1 2A (0, -a )、A (0, a)12轴长虚轴的长=2b实轴的长=2a焦占八、八、F (-c,0 )、F (c,0 )1 2F(0,-c)、F (0,c)1 2焦距FF = 2c (c 2 = a 2 + b 2)1 2对称性关于x轴、y轴对称，关于原点中心对称离心率e = J 徉(e 1)a a 2渐近线方程y = 叭ay = -x b5、实轴和虚轴等长的双曲线称为等轴双曲线.6、平面内与一个定点F和一条定直线l的距离相等的点的轨迹称为抛物线.定点F称为抛物线的

4、焦点，定直 线l称为抛物线的准线.7、抛物线的几何性质:y 2 = 2 pxy 2 = 一 2 pxx 2 = 2 pyx 2 = 一 2 py标准方程(p 0)(p 0)(p 0)(p 0)图形Xk ; jn j圭顶点(0,0 )对称轴x轴y轴焦占八、八、F匕,01 2丿F f 一 匕,01 2 /F f 0, P1 2丿F f 0,-上I 2 /准线方程Px =-2x =匕2y =-匕2y =匕2离心率e = 1范围x 0x 0y 0）上，焦点为F，则|PF|二x + ；0 011 o 2若点P（x , y ）在抛物线X2 = 2py （p 0）上，焦点为F，则|PF| = y +仝o 0

5、1o 21. 值范围。圆锥曲线的方程与性质常用结论A. 常见结论：X 2 y 2x 2y 21与椭圆一 +厂=1 （ab0）共焦点的椭圆方程可设为：+= 1a 2 b 2a 2 + kb 2 + k中心在原点，坐标轴为对称轴的椭圆、双曲线方程可设为唧卡亠勞2=1（mo,nO）x 2 y 2 -x 2y 22. 与厂=1共渐近线的双曲线方程=九（九H 0 ）.a 2 b 2a 2b 2x 2 y 2x 2y 2与7 = 1有相同焦点的双曲线方程一=1 （ k 0)顶点0的两条互相垂直的弦，则直线AB恒经过定点 S 见B. 直线与曲线方程的位置关系：1方法一是方程的观点，即把曲线方程和直线的方程联

6、立成方程组，利用判别式来讨论位置关系.(1) 相交：心直线与椭圆相交；人沁二直线与双曲线相交，但直线与双曲线相交不一定有心=0，当直线与双曲线的渐近线平行时， 直线与双曲线相交且只有一个交点，故A0是直线与双曲线相交的充分条件，但不是必要条 件；A、 n直线与抛物线相交，但直线与抛物线相交不一定有A A ，当直线与抛物线的对称轴平行时， 直线与抛物线相交且只有一个交点，故A也仅是直线与抛物线相交的充分条件，但不是必 要条件(2) 相切：心直线与椭圆相切；心=0直线与双曲线相切；A =直线与抛物线相切；(3) 相离:心 0(x1,y1) ,B(x2,y2)，则 x + x = 2(a + p)，

7、又 y1=x1-a,y2=x2-a,11 2 2 1 2 1122x x = a 2v 1 2.I AB I二(x x )2 + (y y )2 ：2(x + x )2 4x x =、. 8p(p + 2a)1212121 20 I AB I 0, /.0 v8p(p + 2a) 2p,解得：-匕a-匕24x + xx =12 = a + p ,32设AB的垂直平分线交AB与点Q，令其坐标为(x3,y3)，则由中点坐标公式得:y = 2 = (x1 一 a)+ (x2 一 )= p.322所以所以 |QM|2=(a+p-a)2+(p-0)2=2p2.又 MNQ 为等腰直角三角形，所以 | QM

8、| = |QN|=2 P ,NAB丄丨 AB I -1 QN I二以 p-1 AB 122即ANAB面积的最大值为U2P 2。（5）求曲线的方程问题1.曲线的形状已知这类问题一般可用待定系数法解决。典型例题已知直线L过原点，抛物线C的顶点在原点，焦点在x轴正半轴上。若点A（-1，0）和点B（0，8）关于L 的对称点都在C上，求直线L和抛物线C的方程。分析：曲线的形状已知，可以用待定系数法。设出它们的方程，L： y=kx（kM0）,C:y2=2px（p0）设A、B关于L的对称点分别为A/、B/，则利用对称性可求得它们的坐标分别为：k 2 -12kA/ (,-k 2 +1 k 2 +1，B （ -

9、16k-,8（k2）。因为A、B均在抛物线上，代入，消去p，得：k2-k-1=0.解得:k 2 +1 k 2 +11 +岛2、骑所以直线L的方程为:y= 土5 x,抛物线C的方程为y2= 半 x.2.曲线的形状未知求轨迹方程典型例题已知直角坐标平面上点Q （2, 0）和圆C： x2+y2=1,动点M到圆C的切线长 与|MQ |的比等于常数九（九0）,求动点M的轨迹方程，并说明它是什么曲线。 分析:如图，设MN切圆C于点N,则动点M组成的集合是：P=M|MN|=九|MQ|， 由平面几何知识可知：|mn|2=|mo|2-|on|2=|mo|2-1,将m点坐标代入，可得: （九 21）（X2+y2）

10、4 九 2x+（1+4 九 2）=0.当九=1时它表示一条直线；当九工1时，它表示圆。这种方法叫做直接法。（6）存在两点关于直线对称问题在曲线上两点关于某直线对称问题，可以按如下方式分三步解决：求两点所在的直线，求这两直线的交点, 使这交点在圆锥曲线形内。（当然也可以利用韦达定理并结合判别式来解决）典型例题已知椭圆C的方程，试确定m的取值范围，使得对于直线，椭圆C上有不同两点关于直线对称。分析：椭圆上两点，代入方程，相减得k=，p=代入得又由解得交点。交点在椭圆内，则有，得（7）两线段垂直问题圆锥曲线两焦半径互相垂直问题，常用来处理或用向量的坐标运算来处理。典型例题已知直线的斜率为，且过点，抛

11、物线，直线 与抛物线C有两个不同的交点（如图）。（1）求的取值范围;为何值时，A、B与抛物线C的焦点连线互相垂直。（2）直线的倾斜角分析：（1）直线代入抛物线方程得，得（2）由上面方程得，焦点为，得 2 n症0 = arctan 或日=兀一 arctan -2或2B:解题的技巧方面在教学中，学生普遍觉得解析几何问题的计算量较大。事实上，如果我们能够充分利用几何图形、韦达定理、 曲线系方程，以及运用“设而不求”的策略，往往能够减少计算量。下面举例说明：（1）充分利用几何图形解析几何的研究对象就是几何图形及其性质，所以在处理解析几何问题时，除了运用代数方程外，充分挖掘 几何条件，并结合平面几何知识

12、，这往往能减少计算量。典型例题 设直线与圆相交于P、Q两点，0为坐标原点，若，求的值。解： 圆过原点，并且，是圆的直径，圆心的坐标为又在直线上，即为所求。评注：此题若不充分利用一系列几何条件：该圆过原点并且，PQ是圆的直径，圆心在直线上，而是设再由和韦达定理求，将会增大运算量。评注：此题若不能挖掘利用几何条件，点M是在以OP为直径的圆周上，而利用参数方程等方法，计算量将很大，并且比较麻烦。二. 充分利用韦达定理及“设而不求”的策略我们经常设出弦的端点坐标而不求它，而是结合韦达定理求解，这种方法在有关斜率、中点等问题中常常用到。典型例题已知中心在原点O,焦点在 轴上的椭圆与直线相交于P、Q两点，

13、且，求此椭圆方程。解：设椭圆方程为，直线与椭圆相交于P两点。由方程组消去后得由，得又P、Q在直线上,(1)把（1）代入，得化简后，得，得把（2）代入，得，解得代入（4）后，解得，得所求椭圆方程为评注：此题充分利用了韦达定理及“设而不求”的策略，简化了计算。三. 充分利用曲线系方程利用曲线系方程可以避免求曲线的交点，因此也可以减少计算。典型例题 求经过两已知圆和0的交点，且圆心在直线：上的圆的方程。解：设所求圆的方程为：即，其圆心为C（）又C在直线 上，解得，代入所设圆的方程得为所求。评注：此题因利用曲线系方程而避免求曲线的交点，故简化了计算。四、充分利用椭圆的参数方程椭圆的参数方程涉及到正、余

14、弦，利用正、余弦的有界性，可以解决相关的求最值的问题.这也是我们常说的 三角代换法。X 2 y 2 r典型例题P为椭圆一 +=1上一动点，A为长轴的右端点，B为短轴的上端点，求四边形0APB面积的最a 2 b 2大值及此时点P的坐标。五、线段长的几种简便计算方法 充分利用现成结果，减少运算过程的方程，方程的两根设为，判别式为,则代入圆锥曲线方程中，得到型一般地，求直线与圆锥曲线相交的弦AB长的方法是：把直线方程J A门+ k 2 ，若直接用结论，能减少配方、开方等运算过程。I a I例求直线被椭圆所截得的线段AB的长。 结合图形的特殊位置关系，减少运算在求过圆锥曲线焦点的弦长时，由于圆锥曲线的定义都涉及焦点，结合图形运用圆锥曲线的定义，可回避复杂 运算。例 、 是椭圆的两个焦点，AB是经过 的弦，若，求值I F A I + I FB I2 2 利用圆锥曲线的定义，把到焦点的距离转化为到准线的距离例 点A (3, 2)为定点，点F是抛物线的焦点，点P在抛物线上移动，若取得最小值，求点P的坐标。