第五章 时间序列的模型识别

《第五章 时间序列的模型识别》由会员分享，可在线阅读，更多相关《第五章 时间序列的模型识别（25页珍藏版）》请在装配图网上搜索。

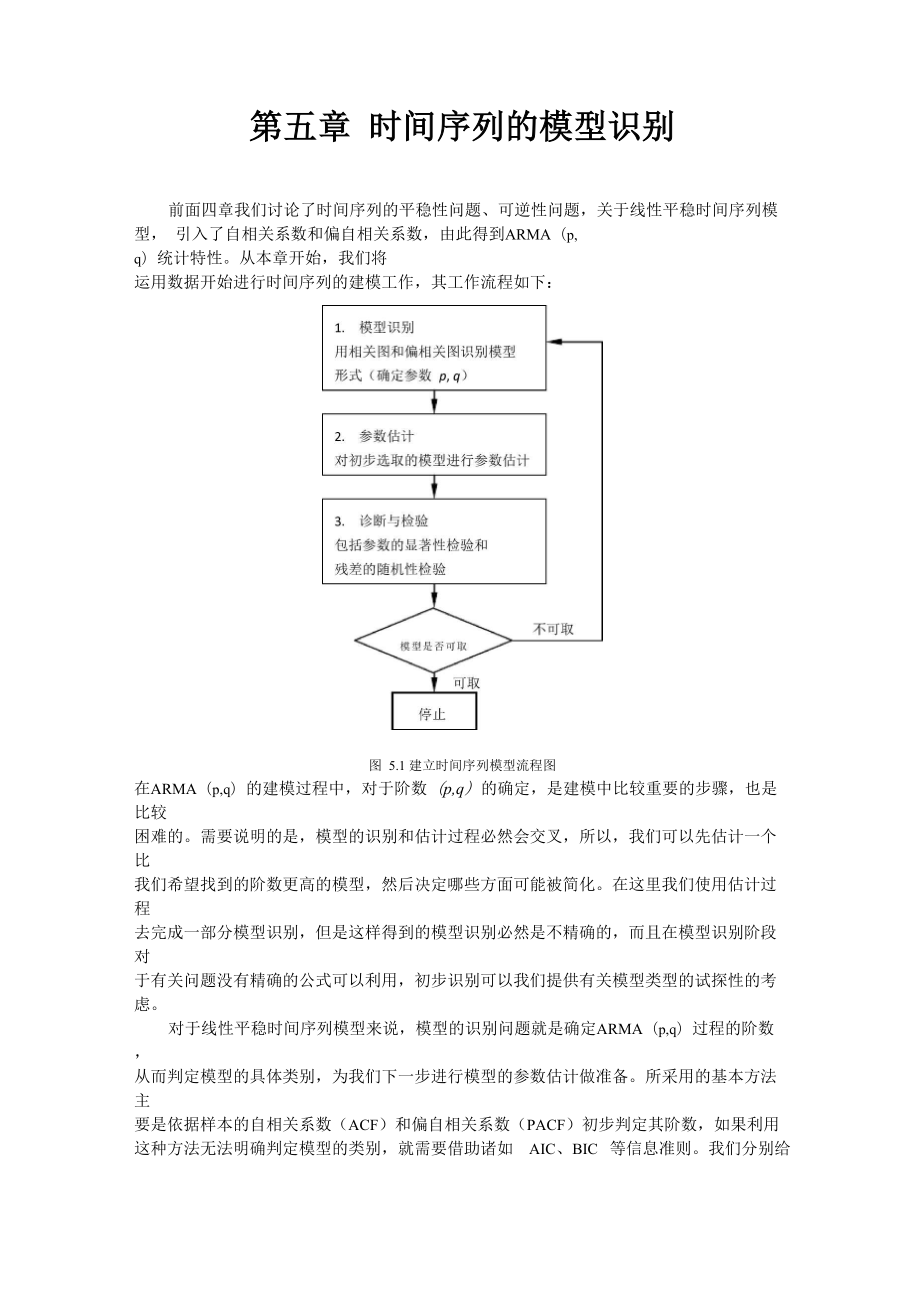
1、第五章 时间序列的模型识别前面四章我们讨论了时间序列的平稳性问题、可逆性问题，关于线性平稳时间序列模型， 引入了自相关系数和偏自相关系数，由此得到ARMA（p, q）统计特性。从本章开始，我们将 运用数据开始进行时间序列的建模工作，其工作流程如下：图 5.1 建立时间序列模型流程图在ARMA（p,q）的建模过程中，对于阶数（p,q）的确定，是建模中比较重要的步骤，也是比较 困难的。需要说明的是，模型的识别和估计过程必然会交叉，所以，我们可以先估计一个比 我们希望找到的阶数更高的模型，然后决定哪些方面可能被简化。在这里我们使用估计过程 去完成一部分模型识别，但是这样得到的模型识别必然是不精确的，

2、而且在模型识别阶段对 于有关问题没有精确的公式可以利用，初步识别可以我们提供有关模型类型的试探性的考 虑。对于线性平稳时间序列模型来说，模型的识别问题就是确定ARMA（p,q）过程的阶数， 从而判定模型的具体类别，为我们下一步进行模型的参数估计做准备。所采用的基本方法主 要是依据样本的自相关系数（ACF）和偏自相关系数（PACF）初步判定其阶数，如果利用 这种方法无法明确判定模型的类别，就需要借助诸如 AIC、BIC 等信息准则。我们分别给 出几种定阶方法，它们分别是（1）利用时间序列的相关特性，这是识别模型的基本理论依 据。如果样本的自相关系数（ACF）在滞后q+1阶时突然截断，即在q处截尾

3、，那么我们 可以判定该序列为MA（q）序列。同样的道理，如果样本的偏自相关系数（PACF）在p处截 尾，那么我们可以判定该序列为AR（p）序列。如果ACF和PACF都不截尾，只是按指数衰 减为零，则应判定该序列为ARMAgq）序列，此时阶次尚需作进一步的判断；（2）利用数 理统计方法检验高阶模型新增加的参数是否近似为零，根据模型参数的置信区间是否含零来 确定模型阶次，检验模型残差的相关特性等；（3）利用信息准则，确定一个与模型阶数有关 的准则函数，既考虑模型对原始观测值的接近程度，又考虑模型中所含待定参数的个数，最 终选取使该函数达到最小值的阶数，常用的该类准则有AIC、BIC、FPE等。实际

4、应用中， 往往是几种方法交叉使用，然后选择最为合适的阶数（p,q作为待建模型的阶数。5.1 自相关和偏自相关系数法在平稳时间序列分析中，最关键的过程就是利用数据去识别和建模，根据第三章讨论的 内容，一个比较直观的方法，就是通过观察自相关系数（ACF）和偏自相关系数（PACF） 可以对拟合模型有一个初步的识别，这是因为从理论上说，平稳AR、MA和ARMA模型的 ACF 和 PACF 有如下特性：模型（序列）AR(p)MA(q)ARMA(p,q)自相关系数（ACF）拖尾q 阶截尾拖尾偏自相关系数（PACF）p阶截尾拖尾拖尾但是，在实际中ACF和PACF是未知的，对于给定的时间序列观测值x，x, ,

5、x，我们1 2 T需要使用样本的自相关系数0 和偏自相关系数对其进行估计。然而由于0 和 kkk. . .k均是随机变量，对于相应的模型不可能具有严格的“截尾性”，只能呈现出在某步之后 kk围绕零值上、下波动，因此，我们需要借助0 和的“截尾性”来判断P 和b 的 kkkkkk截尾性，进而由此可以给出模型的初步识别。首先，我们需要给出样本的自相关系数p 和 k 偏自相关系数 的定义。kk设平稳时间序列X 的一个样本x, x。则样本自协方差系数定义为t 1 T(5.1)V 二 1T (x x)C- x ) 1 k T 1k T jj+ky： 1kT1kk其中x =1 X为样本均值，则样本自协方差

6、系数& 是x 的自协方差系数y 的估T jktkj=1计。样本自相关系数定义为p=VjV0，|k| T 1（5.2）是X 的自相关系数P 的估计。tk作为X 的自协方差系数y 的估计，根据数理统计知识，样本自协方差系数还可以 tk写为Y =1 尸 C 一 x)C 一 x)1 k T -1k T 一 k i jj+k(5.3)Y =Y , 1ko,考查e ,e ，ekkp+l,p+1p+2, p+2p+M, p+M八1八中落入 或e Po时,0， 0， ， 0中满足不等式p0+1,p0+1p0+2, p0+2p0+M,p0+Mkk的个数占总数 M 的 68.3或 95.5，则可以认定ekk 在p

7、o处截尾，由此可以初步判定序列X 为AR(p )模型。t0对于样本的自相关系数p ，由第二章的Bartlett公式,k对于q 0,1 + 2 p 2 j j=1进一步地，当样本容量T充分大时，p 也满足 k6 N(0,l;T)k5.8)5.9)类似于(5.6)或者(5.7)式，对于每一个q 0，检查P，P ，.q+1q+2中落入或者|pJ /T V8289 Q 0.89 68.3%，故该时间序列初步判定为AR（1）模型。1 _ 1v T 273_ 0.0605 的有 9 个，例5.2某时间序列数据（T=273）的样本自相关系数和偏自相关系数计算数据如下：表 5.2 某时间序列数据的样本自/ 偏

8、自相关系数样本自相关系数样本偏自相关系数k/Xpkk/Xpkk/Xekkk/Xkk10.8290.4610.8290.1920.45100.642-0.68100.0130.047110.633-0.1211-0.014-0.26120.4540.0612-0.035-0.41130.165-0.02130.026-0.3614-0.1160.18140.057-0.1515-0.3070.2015-0.0680.1680.04由上表知，样本自相关函数叫呈拖尾状，而从15个偏自相关系数的绝对值来看，除必，6显著地异于零之外，其余13个中绝对值不大于229 _ 0.692 q 68.3%，故该时

9、间序列初步判定为AR（2）模型。例5.3 某车站1993-1997年个月的列车运行数量数据共60个，见表5.3，试对该序列给出初步的模型识别。k12345678910观测值k观测值k观测值k观测值k观测值k观测值1196.8111206.5211238.9311261.6411183.0511306.01181.3121204.0221267.5321274.5421228.0521209.01222.6131234.1231200.9331196.4431274.0531248.01229.3141146.0241245.5341222.6441218.0541208.01221.51513

10、04.9251249.9351174.7451263.0551231.01148.4161221.9261220.1361212.6461205.0561244.01250.2171244.1271267.4371215.0471210.0571296.01174.4181194.4281182.3381191.0481243.0581221.01234.5191281.5291221.7391179.0491266.0591287.01209.7201277.3301178.1401224.0501200.0601191.0表5.3某车站1993-1997年个月的列车运行数量数据（单位：千列

11、千米）图5.3， 5.4分别为原始数据和平稳化以后（第8章将给出具体平稳化方法）数据的散点图。图 5.3 列车运行数量数据 图 5.4 平稳化列车运行数量数据 经过计算，其前20 个样本自相关系数和偏自相关系数如下表5.4平稳化列车运行数量数据样本自/偏自相关系数样本自相关系数样本偏自相关系数k/XPkk/Xpkk/X0kkk/X0kk1-0.68511-0.0361-0.68511-0.13020.341120.1562-0.243120.1393-0.19313-0.1653-0.139130.13640.042140.0384-0.20814-0.1845-0.068150.0015-0

12、.31315-0.12060.19916-0.02760.04616-0.0127-0.221170.1437-0.030170.19680.18518-0.1308-0.037180.0259-0.130190.0049-0.00219-0.143100.037200.02110-0.04220-0.073由上表知，样本自相关函数呈拖尾状，而从20个自相关系数的绝对值来看，样本自相kk关系数在最初的2阶明显的大于2倍标准差范围，即(-0.26, 0.26),而后95%以上的 k样本自相关系数0k都落在(-0.26, 0.26)内，并且由非零样本自相关系数衰减为在零附近小 值波动的过程非常突然

13、，这时通常视为自相关系数P 截尾，故该时间序列初步判定为 kMA(2)或 MA(3)模型。5.2 F 检验法利用F分布进行假设检验是实践中经常使用的统计检验方法，在回归分析中，往往用F 检验来考察两个回归模型是否有显著差异，因此常被用来判定ARMA模型的阶数。考虑如下线性回归模型y = a X +a X + + a X + 8(5.10)1 1 2 2 n nY = (y,y,y )t为N个独立的随机观察值，X = (X ,X，,X )T , i = 1,2,r为 1 2Nii 1i 2iNr个回归因子，8二(8 ,8，,8 ) T为模型残差。设&是模型(5.7)中参数 1 2 Na - Q,

14、a ,a )t的最小二乘估计，为了检验其中后面s个元素对因变量的影响是否显 12 r著，设去掉此S个因素的线性回归模型为5.11)y a X + a X + + a X + 81122r - sr - s其中模型(5.11)的参数a 的最小二乘估计为&。因此，检验模型(5.10)与(5.11)是否有 显著差异等价于检验原假设，即H :a a a 0(5.12)0r -s+1r -s+2r是否成立。为此，考虑上述两个模型的残差平方和Q0与Q,于是有Q =(y -a X -a X a X )(5.13)0 t 1 1t2 2 tr rtt12Q =(y aX aX a X )(5.14)1t 1

15、1t2 2tr -s r -s,tt1借助回归分析中残差平方和的分布结论：Q2X2(N - r)，Q与Q - Q相互独立,0 0 1 0 且当原假设H为真时，Q - Qa2x2(s)，因此有：0 1 05.15)5.16)Q1 - Qo /-QF(s,N - r) s N - r据此构造统计量F Q1-Qo /2s N -r对于预先给定的显著性水平a ,由附录F分布表查出满足P(尸讥)a(517)若F F (s,N - r)，则拒绝原假设Ho，即后面s个因素对因变量的影响是显著的；若 a0F F (s,N - r)，则接受原假设也，即这s个因素对因变量的影响是不显著的，表明模型 ao(5.11

16、)是合适的。521 AR(p)模型定阶的F准则1967年，瑞典控制论专家K.J.Astr&m教授将F检验准则用于对时间序列模型的定阶。 设X (1tN)是零均值平稳序列的一段样本。并用模型AR(p)X =0 X +0 X +0 X +(5.18)t1 t12 t2p tpt进行拟合。根据模型阶数节省原则(parsimony principle),采取由低阶逐步升高的“过拟合”办法。先对观测数据拟合模型AR(p)(p=1, 2,.),用递推最小二乘估计其参数0 .(1 j 化就拒绝假设H0，即AR(p-1)是不适合模型；若F F，这表明F检验显著，表明AR(1)模型是不适用的，应改用AR模型。计

17、算得 aF=3.86则H0不成立，模型阶数仍有上升的可能；否则H0成立，即ARMA(p-1，q-1)是合适的模型。5.3 信息准则法5.3.1FPE 准则法前面两节中模型的定阶都采用统计检验手段，在给定显著性水平a下作假设检验，带 有一定的人为性和主观性。而FPE、AIC和BIC准则都避免上述的缺陷。1969年，日本统 计学家赤池(Akaike)提出了一种识别AR模型阶数的最终预报误差准则(Finial Prediction Error)，简称FPE准则。其基本思想是用模型一步预报误差的方差来判定自回归模型的阶数 是否适用，一步预报误差的方差愈小，就认为模型拟合愈好。设随机序列X所适合的真实模

18、型为AR(p)，即X =0 X +0 X +0 X +8t 1 t -12 t - 2p t - pt其中E( ) = 0， E(82)= Q2。设0的估计值为0. (1W i W p)。用X表示时刻的 ttiit一步预报值，则有幺(1) =6 X +0 X +0 X(5.23)t1 t- 12 t- 2p -t p可以证明一步预报误差的方差为pEX- X (1)2 沁(1 +)b 2(5.24)t+1tn可以证明，当样本总量n充分大时有EQ2沁(1 - J2(5.25)n上式表明 2/(1 -匕)是C 2的无偏估计。在式(5.21)中用无偏估计来代替 2便可得到nEX-文(1)2 沁(1 +

19、 匕)(1 -上)-1 2(5.26)t+1 tn n因而将 FPE 准则定义为FPEp入 n + p = 0 2-n - p5.27)n + p其中可以看出，系数随着p的增大而增大，而当阶数由低阶至高阶增加时，AR(p)n-p模型残差方差& 2开始是随着p的增大而减小，但当p超过序列X/勺真正模型阶数p之 后，& 2就不会再减少了，这时工上将起主导作用。最终，使FPE取最小值的那个p就 n- pp可以判定为模型的最佳阶数。根据经验，当样本点数n=100200时取预先设定的样本上限L =；当n=50100ln 2nn时，取L = 3 如果FPE的数值从p=1就开始上升，则可以判定模型阶数p=1

20、。若FPE的值随p增 pp加而一直下降，则很可能是由于实际数据序列不宜采用AR序列来描述。如果在某一p的FPE值下降很快，以后又有缓慢地下降，则可以将这个p值作为模型的阶。如果随p的增 p加FPE的值上、下剧烈跳动，取不出最小值，这很可能是由于样本数据长度n太小引起的, p可增大样本长度后再进行定阶。例55 根据某实测数据序列拟合的AR(p)(p=l,2,.,10)模型的02和FPE结果如下pp表所示：表 54拟合各阶AR(p)模型的0 2和FPEpPp八O 2PFPEP01.72031.720310.50970.520220.47900.498930.47280.502740.47080.5

21、10950.47050.521160.47050.531870.46790.539980.46640.549390.46640.5607100.44530.5465由表中可以看出，曲2随着p的增加持续下降，但是FPE在p=2时取得最小值，这提 pp示着模型取为AR(2)较合适。5.3.2 AIC 准则法AIC准贝9 (An information criterion)是由日本统计学家赤池弘次(Akaika)在1973年提出 的。该准则既考虑拟合模型对数据的接近程度，也考虑模型中所含待定参数的个数，适用于 ARMA (包括AR和MA)模型的检验，下面我们对AIC准则理论给出一般性的介绍。设n维随

22、机向量X的概率密度属于函数族f (冲)，屮，f (冲)与f (-；0)之间的Kullback-Leibler 指标定义为d(屮0 ) = A(屮0 )-A(O0 )(5.28)其中A(屮 O)二 EO(-2ln f (X冲)二 J-2ln(f (X冲)f (X;O)dX(5.29)Rn是f (；屮)相对于f (;0 )的Kullback-Leibler指标，根据Jensen不等式有：d (屮 0) = J - 2ln(Rnf (X ;y) f (X ;0)f (X ;0 )dX-2ln J (f (X)f (X;0)dX-2ln J f (X ;屮)dXRn5.30)=0其中的等号当且仅当f

23、(X ；屮)=f (X ;0 )时成立。假设所有观测X , X，,X来自一参数向量为0二(PQ2)的ARMA过程，真实的阶1 2 n数为(p,q)，令0二(p，&2)为0基于X ,X，X的极大似然估计，Y,Y,丫为该过1 2 n 1 2 n程的样本实现，贝-2lnL (P,d2) = -2lnL (P,&2) + &-2S (P)-n(5.31)YXY其中：l( ,e ,& 2)=寸(2兀&2)“r r 强2& 20n1匕(学Ij=1jrj1& 2 二 n-is($,0)s(&,e) = r(X X )2/r=1j jj1j=1r =E(X X )2/& 2nn +1n +1这样，Ee(MP)

24、= E卩&2(-2lnLy(P，&2)=E(2lnL (p，&2) + EP ,& 2X-n5.32)在大样本逼近的情形下，EP，& 2(2( p + q + 1)nn pq25.30)从而，2lnL (p，&2) + 2(p + q +1)n/(n p q 2)是 Kullback-Leibler 指标E (A(eP)xe的渐进无偏估计。前面的推导是建立在真实阶数为(P，q)的基础上的，因而可以选择能够极 小化如下AICC(P)函数的(P，q)，或者极小化等价AIC(P)统计量的(P，q):AICC (P ) := 2ln L (P,S (P)/n)+2(p+q+1)n/(n pq2)(5.

25、31)XXAIC(P):=2lnL (P，S (P)/n)+2(p+q+1)(5.32)XXAICC(P)和AIC(P)也可以定义为以& 2的估计值代替公式中的SX(P )/n的形式，因为当 设定&2 = S (P)/n时，AICC(P)和AIC(P)同时极小化。X对 于 自 回 归 模 型 来 说 ， AIC 存 在 着 过 拟 合 p 的 倾 向 ， 惩 罚 因 子 2(p + q + 1)n /(n p q 2)和2(p + q +1)在n T 时是渐进等价的，但AICC统计量对 高阶模型会有更极端的惩罚效果，这将抵消AIC的过拟合倾向。从上述可以看出， AIC 准则的一般形式可表为:A

26、IC=-2ln (模型最大似然度)+2 (模型独立参数个数)(5.33)将其具体运用到AR(p)模型的定阶时，设观测数据序列X为零均值平稳序列，其中的一组样本数据为x ,x ,x，设定一个拟合模型的最高阶数L,则AR(k)模型AIC定阶1 2 T步骤如下：(1) 计算样本自协方差系数/ (0kL)和样本自相关系数P (0kL)kk(2) 利用递推算法计算偏相关函数0 (ljklkL)kj(3) 令&2 =70 7(5.34)k 0 kj jj=1其中& 2是AR(k)模型残差方差，记k2kAIC (k) = In & 2 + - k T(0 k L)5.35)在1kL范围内，如果当k=p时，A

27、IC(k)取得最小值，则适用的模型为AR(p)。533 AIC准则用于ARMA(p, q)模型的定阶根据取得的观测数据样本X , X , X，计算出拟合残差方差& 2的估计值& 2，设定1 2 N拟合模型的最高阶数L,在0pL，0qL范围内，计算AIC(p，q) = In & 2 + 2( p q + D(5.36)kN如果当p=p0，q=q0时，AIC(p，q)取到最小值，则表明适用的拟合模型为ARMA(p, q)。 如果时间序列均值不为零(卩北0)，则均值应作为一个独立参数进行估计，此时有AlCp, q) = ln & 2 + 2(卩 + ； + 2)(5.37)kN由此可见，AIC准则函

28、数通常由两项构成。第一项体现了模型拟合的好坏，它随阶数的 增大而至小；第二项体现了模型参数的多少，它随阶数的增大而变大。取二者的最大值意味 着上述两个量的一种平衡。从k=0开始逐新增加模型阶数AIC(k)的值是下降的，因为此时 起决定性怍用的是第一项，即模型残差方差。当阶数k达到某一值k0时，AIC(k)达到最小, 然后，随着阶数 k 继续上升，残差方差下降甚微。起决定性作用的是第二项，从而 AIC(k) 的值随k而增长。此外，使用AIC准则需要注意以下几个问题：(l) AIC准则要求预先设定模型阶数的最大范围L。根据经验可知，阶数上限取、帀,N/10,logN均可。在比较AIC大小的过程中，

29、如果已接近阶数上限仍不能确定AIC 的极小点，则应加大上限，继续进行比较。(2) AIC 准则要求参数由最大似然无法解释，但当序列不服从正态分布时计算表明该 准则对于最小二乘法估计也仍然适用(3) AIC准则是模型优化的一种宏观度量，但不宜机械地以绝对最小值来选择模型阶数， 而是要在所对应的模型进行多次比较后，确定合理的模型阶数以及相应参数。例56 根据某观测数据序列(T=176)拟合出若干个AR(p)模型，其模型参数估计值、 残差方差值以及AIC值如下表所示。表5.7某序列模型的AIC定阶结果参数值AR(p)模型AR(1)AR(2)AR(3)AR(4)AR(5)010.80861.33061

30、.28971.28531.2851八2-0.64550.56110.59950.5994八03-0.06350.02480.0231八04-0.06840.0649八05-0.0027cf 2418.17243.92242.94241.80241.80AIC1074975.4976.7977.9979.9根据模型定阶的AIC准则，由上表中AIC的数值可以看出，最合适上述观测数据序列 的模型结构应是二阶自回归模型，即 AR(2):X -1.3306X -0.6455X =tt1t2t5.3.4 BIC 准则法理论上已经证明，AIC方法不能给出相容估计。也即当样本容量T fg时，采用AICAkai

31、ke(1976 年)和5.38)方法定出的模型阶数估计值，并不能依概率收敛到真值。对此E .J.Haman(1979年)等学者又提出了 BIC准则BIC 准则函数的定义如下BIC(p) = log 2 + p log T若某一阶数 p 满足0BIC(P ) = min BIC(p)(5.39)01 p 2，因此AIC达到极小时所对应的阶数(Po)往往比BIC准则相应定出的阶数(P：)高，即p P00这说明对同一数据序列进行拟合，用AIC准则往往比用BIC准则确定的阶数高。此外，还 可以定义其他类型的准则函数，如BIC(p) = logc 2 + CP log T(5.40)其中 c 为给定常数

32、。必须指出，定义不同的准则函数，其目的是为了对拟合残差与参数个数之间进行不同的 权衡，以体现研究者对残差与阶数两者重要性的不同侧重。当然，用不同准则挑选出的最优 模型，其渐进性质是不同的。例如当样本数据N充分大时，用AIC准则挑选的最佳模型 的阶数往往是过相容的，也就是说，选定的阶数往往比真实模型的阶数高。而用 BIC 准则 确定的最佳模型往往是相容的，也就是说，选定的阶数往往比较接近真实模型的阶数。在实际问题中，对不同阶数模型得到的准则函数值，往往不是理想的下凸函数，而是总 的趋势符台下凸函数变化规律，同时具有随机起伏，有时可能出现准则函数值达到某值后 没有明显的增长趋势，而是随机地起伏摆动

33、。遇到这种情况，如果适当地增加式(5.40)中 常致c，可使准则函数值在后一段有较明显的增长趋势。习题五5.1设X 为零均值平稳序列，给定长度T = 100的样本，计算得样本自协方差系数如下，t试求样本偏自相关系数的估计，并对序列服从哪种模型进行识别。(1) 吟=1.4，吟=0.77，V =0.41，吟=0.2，吟=0.06，V =-0.05，V =-0.140123456(2) V =198， V =0.41， V =-125， V =-0.71， V =0.61， V =0.65， V =-02701234565.2已知某序列X (T = 96)的样本自相关系数和偏自相关系数如下，试对序列

34、X 给出tt初步的模型识别。样本自相关系数样本偏自相关系数kPkkzpkkz0kkkzkk10.42811-0.04810.42811-0.08620.29112-0.19720.13112-0.18830.188130.07030.029130.13540.04214-0.0574-0.09314-0.00250.08715-0.00650.08615-0.04860.048160.1526-0.001160.17070.002170.1417-0.038170.07180.046180.11780.04518-0.04690.085190.06590.08519-0.066100.004200.08510-0.083200.113