第二章变分原理

《第二章变分原理》由会员分享，可在线阅读，更多相关《第二章变分原理（38页珍藏版）》请在装配图网上搜索。

1、第二章变分原理变分原理是力学分析中重要数学工具之一，能量法、有限元法、加权残值法等力学方法都是以变分原理为数学工具的。变分法的早期思想是 Johann Bernoulli在1696年以公开信的方式提出最速降线命题，并在1697年进行了解决。关于变分法的一般理论是Euler于1774年、Lagrange于1762年共同奠基的，我们称之为Euler-Lagrange变分原理。1872年Betti提出了功的互等定理。1876年意大利学者 Castigor提出了最小功原理。德国学者Hellinger于1914年发表了有关不完全广义变分原理，后来美国学者 Reissner发表了与Hellinger相类似

2、的工作，此工作被称之为 Hellinger-Reissner变分原理。我国学者钱令希于1950年发表余 能原理”论文。我国学者胡海昌于1954年发表了有关广义变分原理的论文，日本学者鹫津久一郎(Washizu)于1955年发表了与有胡海昌相类似的工作，此工作被称之为胡-鹫变分原理。1956年Biot建立了热弹性力学变分原理。1964年钱伟长提出用 Lagranger乘子构造广义分原理的方法。1964年Gurtin提出了线弹性动力学变分原理。1967年意大利学者 Tonti提出了四类变量的广义变分原理，在这类变分原理中，位移、应变、应力及Beltrami应力函数都是变分变量。2.1历史上著名的变

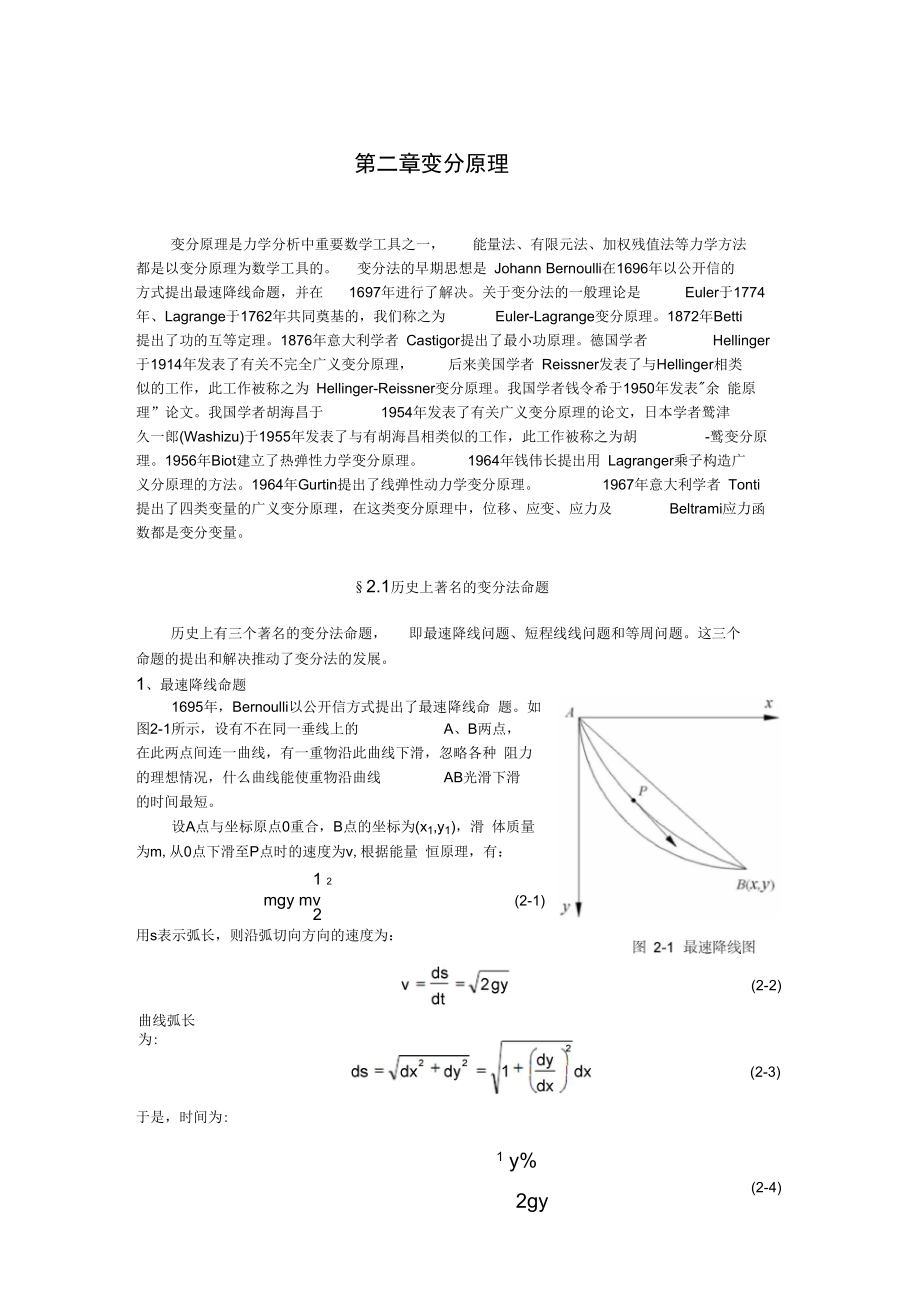
3、分法命题历史上有三个著名的变分法命题，即最速降线问题、短程线线问题和等周问题。这三个命题的提出和解决推动了变分法的发展。1、最速降线命题1695年，Bernoulli以公开信方式提出了最速降线命 题。如图2-1所示，设有不在同一垂线上的A、B两点，在此两点间连一曲线，有一重物沿此曲线下滑，忽略各种 阻力的理想情况，什么曲线能使重物沿曲线AB光滑下滑的时间最短。设A点与坐标原点0重合，B点的坐标为(x1,y1)，滑 体质量为m,从0点下滑至P点时的速度为v,根据能量 恒原理，有：1 2mgy mv(2-1)2用s表示弧长，则沿弧切向方向的速度为：(2-2)曲线弧长为:(2-3)于是，时间为:1

4、y%2gy(2-4)下降时间为:TX00(2-5)经过求解，最速降线为圆滚线，其参数方程为：Cxsi nv2Cy 二 1 - cos，(2-6)2、短程线命题设x,y,z =0是如图2-2所示的曲面，在此曲面上有 A、B两点，试问如何连接可使 此曲面上A、B两点间的距离最短。设A点的坐标为A xi, yi, zi、B点的坐标为Bx2,y2,Z2，在曲面上A、B两点的曲线长度为：I dxX2其中，y = yx,z=zx是满足曲面x, y, z = 0的约束条件。3、等周命题等周命题为在长度一定的闭合曲线中，什么曲线围成的面积最大。(2-7)图2-2短程线设所给曲线的参数方程为 x = xs,y

5、= ys，因这条曲线是封闭的，在这条曲线的始端和末端，有x So二xsi,yso = y s。该曲线周长为:ds(2-8)由于该曲线封，根据格林公式:dY dX dxdy =- Xdx Ydydx dx(2-9)该曲线所围成的面积为:1j1“1JJdxdy =- 川1+1 dxdy = q(xdy-ydx)= JQ 2Q2? ss12汕ds(2-10)于是等周问题可以归纳为在满足x sd =xsi,ys)= ys和式(2-8)条件下，从所有可能函数中选择一对函数使面积最大。2.2泛函的概念在函数论中，自变量 x对应着另一变量y，则变量y称为自变量x的函数y(x)。假如 自变函数y(x)对应着另

6、一个函数丨ly(x),则丨I ly(x)称为泛函。函数是变量与变量之间 的关系，泛函是变量与函数之间的关系。泛函是函数的函数，是函数的广义函数。通过微分学和变分学对比，可理解变分特性。2.2.1微分和变分函数y(x)的自变量x的增量 x是 x = x-x1，当x是独立变量时，x的微分等于x的 增量，即ex -.x ；泛函丨【ly(x) 的自变函数c的增量在它很小时称为变分，用：y(x)或简单地用:.y表示。变分:.y等于y(x)与跟它相接近、并通过边界的另一个函数y1(x)之差，即 y(x) = y(x)-y1(x)。特别指出的是，变分y(x)不是常值，而是通过边界条件的函数。两个自变函数相接

7、近的意义可有不同的理解，最简单的理解是在任意X值上y(x)和y, (x)之差很小，即：y(x)-%(x)(2-11)这种接近称零阶接近度，如图2-3所示。很明显，这时之差 y (x) - y, (x)不一定是微量。如果满足零阶接近，同时满足自变函数的斜率也很接近，即：y(x) yi(x)乞； (2-12) y (x) - yi(x)乞；POx图2-4 一阶接近度这种接近称一阶接近度，如图2-4所示。图2-3零阶接近度依次类推，k阶接近度要求零阶至k阶导数之差都很小。6y = y(x)-yi(x)“6yy1(x)-yi1(x)s(2-14)y2 = y2(x) y；(x) 0时-(x ：x) 0

8、， 此时可称y(x)是可微，相应有：Ly =dy = A(x) = x = y dx 巴二佃卫二A(x) dxxD x也可以说，对于可微函数，函数的微分是函数增量的主部分，即线性项。 函数的第二定义是设；是为一小参数，将 y(x 凡x)对；求导数，即dy(x + x)x + Mx )y(x 汇x )y * 忙x i-)x(x ： _x) :；当；趋近于零时y(x+x)= y (x)x(2-17)(2-18)(2-19)这就说明，y(x ：汇x)在；=0处对:的导数等于y(x)在x处的微分。；称为拉格朗日乘子， 此法称为拉格朗日乘子法。泛函的变分也有类似的两个定义。第一个定义：自变函数y(x)的

9、变分:y(x)所引起的泛函的增量，即：:二二二y(x) 、y(x) I ly(x) I(2-20)类似地，其可展开为线性项和非线性项- = Ly(x),、 y(x) J - ly(x),、y(x) 1、Ymax(2-21)其中L是对:y(x)的线性泛函项，而 1是非线性泛函项，是 :y(x)的同阶或高阶微量，当 、：y(x) 0时：ymax 0，同时也趋近于零，这时泛函的增量等于、：y(x)的线性部分Ly(x).y(x) 1,叫做泛函的变分，用匸来表示。、二二二0 -二 ly(x) 、y(x)ly(x) I- Ly(x),、y(x) 1(2-22)所以泛函的变分是泛函增量的主部，而且这个主部对

10、于函数变分：y(x)来说是线性的。第二个定义：泛函变分是y(x) ny(x) 1对；在；=0处的示导值。泛函的增量用微小参数:表示为：二=二 2( x) ；、y( x)二-y( x)二Ly：x,；、 y(x)- y(x),y】(；x)maxy因为泛函导数是:/ ly(xp ； y(x)对；的导数在；=0时的值，于是有y( x)；、.y(x)L 淙 y( x) ； y( x), y (Xa)dzczy(x),；、. y(x)；、. m%x (x) cz因为线性项Ly(x), ；、： y(x) I对、:y(x)是线性的，故L y(x), ；、. y(x) I - ；Ly(x),、. y(x) 1并

11、且当；.一.0 时_y(x), ；、： y(x) 1 0，: ymaxr 0，得二 y(x)丄曲y(x) J - L y(x),、y(x) 1 cz由此得拉格朗日的泛函变分定义为二=y(x)亠 M y(x) I 门0 = Ly(x),、y(x) .1c y (x)(2-24)(2-25)(2-26)(2-27)2.2.2变分运算规则d(x)普dyi(x)dx= y(x) _y1(x)=、dy(x)-dx(2-28)dUy(x)警dx_ dx因此，变分和导数 的运算可换，变分的导数等于导数的变分。dx同理有：(2-29)L y(x) l - y(x)L y(x)丨 _ yn (x)其它运算规则如

12、下：(2-30)1 、(二二 2)= 二1二22 .2)-仁二23、(二昇二？)=(二 2、； 一二二 2)/二 24-二门二宀二5、(yn)*y)nX2X26 、 dxdxXXi(2-31)2.2.3极大极小一一极值问题与函数的极大、极小问题相类似，泛函也有极大、极小问题。如果任何一条接近自变函数的变分:y(x)是x的函数，于是可以用x求导数y二yo(x)的曲线y(x)的泛函值11 y(x) 1不大(或不小)于y(x)的泛函11 :yo(x)，即二二二y(x)二二一yo(x) _0(或-0),则泛函|丨j(x)在曲线y(x)上达到极大(或极 小)值，而且在 y =y0(x)上泛函的一阶变分等

13、于零由.=0(2-32)因为函数接近度有零阶和高阶之分，所以变分分为强变分和弱变分。对于y(x) - y0 (x) 名的零阶接近度的变分称为强变分，这样得到的极值叫强极值。如果是一阶接近度，即y(x) - y(x)1(2-38)x2:F:F令二=x( y y)dx(2-39)x:y:y2_x2;：2F2：乍 ；：2F 25 = J |=y) +2=v5y6y + =衍)dx为: y：y: y这时式(1.3.6 )可以写成.一=厂 1 .2_ (2-40)2!其中、二，上一,称为一阶变分，二阶变分等。 根据式(2-34)的泛函极值条件，=0,即x2 _F : F ( y y)dx=O(2-41)

14、wcycy关于泛函的一阶变分式(2-39)或式(2-41)可由导数的概念获得。令F(x,y,z)是自变量x,y,z的函数，则其全导数为(2-42)cF3F3FdF (x, y, z) dx dy dzexdycz令泛函 F(x, y, y是函数y(x)的函数。假如F不仅与y有关，同时与其导数有关，这时 泛函一阶变分自变函数可视为y(x)和其导数y(x)的函数。因此可以把微分符号 d用变分符号：来代替，而、；x=：0，因泛函的变分只与 y(x)和y(x)的变分有关，故泛函变分为cFcFF 二、.y、. y假如泛函含有y,y,y，则:F:F 6F(x, y,y , y )=6y+,5y+, 6yc

15、ycycy(2-43)(2-44)对式(2-42 )的第二项进行分部积分，得(2-45):主、y =壬、y：2- x2 Q(兰)、y dx:y 7x11 Ldxfy把上式代入式(2-42)中，得Xi.:F:y罟(M)、ydx辽皿“dx :y: y(2-46)上式第二项是边界条件式，当给定边界条件情况下在x = %和x = x2处y = 0，(式(1.3.5),即第二项等于零，这个边界条件称为基本边界条件。当没有给定基本边界条件时y在x =为和x = x2处: y = 0处可能不等于零，则、二=0的条件必须要求在边界处.:F /=0,这一边界条件称为自然边界条件。今后将看到弹性力学问题的基本边界

16、条件为位移(包括转角)，自然边界条件为力(包括弯矩)。式(2-46)的第一项中:y是x的函数，它不能等于零，故-=0的条件是(2-47)这个方程称为欧拉方程， 就是说，泛函极值的积分方程转换成欧拉方程一一微分方程。 这是 1744年欧拉提出的著名方程，后来拉格朗日用拉格朗日法简捷地得到相同结果( 1755年)， 所以这个方程又称为欧拉-拉格朗日方程。应当指出，假如原来的泛函的积分方程含有一阶导数， 则欧拉方程将含有更高一阶导数。 欧拉方程式(2-47)是泛函极值的条件式。为判定所得解为极大还是极小，需要考虑二阶变分2 :-的符号。因所得的解已满足、二=0，由式(1.3.9)1 2二.2!2因此

17、，若对于任意、：y(x)有:. - o,则解使二为极小，反之极大。 假如泛函还含有两阶导数，则其泛函数为(2-49)口y(x) = ( F x, y(x), y(x), y (x) dx端点上的边界条件为y(xj =力, y(xj = yi,y(x2)十Iy(X2) *2(2-50)根据式(2-46)，一阶变分x2 ；_F； F ； F二iy(x)亠 c y y y )dx(2-51)人讷讷cy和前面推导一样,上式的第二项进行一次分部积分,第三项进行两次分部积分，并考虑边界条件，得欧拉方程(2-52).:Fd?Fd2;：F门(：) 2 =0ydx: ydx: y这一欧拉方程与式(2-47)比校

18、，上式多一个全微分项，它是(2-51)的第三项进行两次分部积分时得到的。壬:y同理含n阶导数的泛函极值的欧拉方程为(2-53)d；:Fd2；:F“ 八n d；:Fxcdx歹d?帚(-1)护护这是函数y(x)的2n阶微分方程，称为欧拉-柏桑方程，未知常数是 2n个，由2n个边界条 件确定。例1连接两点的最短曲线长度根据数学理论，两点间曲线长度用积分表示为：L =广 J1 +y，2 xx泛函只含有y,其欧拉方程为dxy/J_y2y 二 GxQ其通解为 其中g,O是由边界条件的两点 X1,y1、 X2,y2确定，最后得2勺；2F6 口 = J IX2 J 十 y 2 _ y2 / =L 2 211

19、y2X2dy 小+y2x2 1-12(1 y2)3/2、y dx 0因此，泛函是最小值。例2 Winkler基础上初等梁的微分方程Winkler基础上初等梁的总势能为：n =1 ei (2o)2dx 1 lkw2dx-dx2 0l0qwdx根据欧拉方程，知 Win kier基础上初等梁的控制方程为:EI4d w4 kw -q = 0 dx(1.3.19)例3双参数地基上初等梁的微分方程双参数地基上初等梁的总势能为:d2w 21dx2)dx 2l 2 lokwdx-jwdx例4双参数地基上 Timoshenko梁的微分方程 2.3多维问题泛函及其极值问题(2-54)2.3.1含有一阶导数的二维、

20、三维泛函w : wJw(x,y)lsF x,y,w(x,y), &(x,y),7；(x,y)自变函数w(x, y)是x，y的函数，它在边界 c上w(x, y)已知。为简便，引进符号w,x：w(x,y)w,y:y(2-55)；：2w:.2 :w_浮w_ 2 ,y显然，式(1.4.1)的一阶变分可写为lewcw,xcw,y上式右第二式用附录A公式(A.4)格林公式进行分部积分，得w,xx,yyw,xy:x :y3n =L，s,x王、wxdy(2-56);F由此得欧拉方程为dn =.L erc erc er L-& wdxdycw & cw,x cy cw,y(2-58)十r一：w ；x ：w,x：

21、y ：w,y(2-59)上式称为奥斯特罗格拉斯基公式 同理，三维问题泛函式的欧拉方程为口 = 一 .x, y,乙 w, Wx, Wy, Wzjdv(2-60)十 rrr.:w ；x ：w,x:y ：w,y ；z ：w,z(2-61)和一维问题欧拉方程式（1.3.15）相比校，二维和三维问题欧拉方程式（144 ）和（1.4.5）各自增加了第三项和第四项，它们的公式结构与一维问题完全相同。应当特别注意的是，多维积分的分部积分过程中采用附录A的格林公式，它对计算力学发展起了重要作用，它的贡献在于使高维变低维，高阶变分变为一阶变分、：W，在以后的有关章节详述。2.3.2含有两阶导数的二维、三维泛函Lw

22、( x, y)=w W,y W,xxW ,xW , yWds(2-62)6wxdxdy = J c c dwdxdys ：Wxs ；:Wx ；x一 nx、. wdc一 .：. wdxdyc cw,xs ex cw,x同理，第三式也用格林公式，代入式（143）中，并考虑到在边界上 :.w =0，得的一阶变分为二lw(x, y) 1 =f 6w + cwcw,y,yw,xx,xx(2-63)-w,xyw,xy,yyds其欧拉方程为frs2FF_+2CWex CW,x CW,yexcw,xx:F2_F +_ _ - 2 x y : w,xy: y； w,yy(2-64)z, w, w,x, w,y,

23、w,z, w,xx ,w,yy, W,zzW,xy , W,xz , W, yz dS(2-65)上式中函数 w（x, y）和它的导数是x，y的函数。 同理，三维情况的泛函-=vF |l_x,y,其欧拉方程为2 2 2-十FFFFFF-T-2dwexcw,xcycw,ycz(w,zexcw,xxccyGW,xyCXcZCW)XZ-2F c2 0GZtW.zz-2 2FF2fytZ CW,yzcyCW,yy上式中自变函数 w和它的导数是x, y, z的函数。2.3.3与时间和空间有关的泛函口 lw(x, y, t)= (2 F x, y,t,w,w,x,w,y,w,xx,w,xy,w,yy,w,

24、t ds(2-67)其欧拉方程为2 2 2.I-L、 .-I-L、.-I-.cj-f-.*.r I-L、.I-L、I-(2-68)十FFFFFF2 2twxcw,x&ycwyctcw,texcwxxxycw,xycycwyy上式中wt=m，自变函数 w和它的导数是x，y，t的函数。 , 建以上都是含有一个自变函数的情况。2.3.4 含有n个自变函数的泛函现有n个自变函数（x）, y2（x）,., yx），其泛函式为 b-=a F（x,y!, 丫2,.小，,丫2,，yjdx（2-69）a其一阶变分为n阳吐8 *弟.yiyi dx（2-70）a y ：y：-x y ：y欧拉方程为:Fd；:F（）=

25、0, i =1,2, .n（2-71）.yidx : yi上式与式（1.3.5）的欧拉方程完全一致，只是yj代替y，并且式（1.4.9）是n个联立方程。含有高阶导数的多维问题 n个自变函数的表达式与式（144）（1.4.7）完全一致，但是它 是联立方程。例1求下列泛函的欧拉方程1 - 2-I s2727xd上式含有w,x和w,y，故由（2-61）,得cw:2； w_ 2y显然，这是在流体、电磁场及热场中常用到的拉普拉斯方程。 例2求下列泛函的欧拉方程2 2 2_ D , ,cwx2w、2 弋 wS ( 2) 2()(一2 S x；xy-y22) -q(x,y)wdxdy上式含有 W和wxx.的

26、泛函，由式（2-61）得欧拉方程_4_4_42. 2WW J W、D w 二 D(r 2 2 24)= q(x,y)excx&ycy这是薄板弯曲微分方程式。例3多质点系的拉格朗日方程理论力学中的拉格朗日方程，可以由式（.2-71）得到。自变量 数y用广义坐标q代替，y用时间的导数qi代替，贝Vb*二二 a L（t,q1,q2,.qn,q,q2,.qn）dt根据式（2-71 ）泛函极值的欧拉方程为x用时间t代替，自变函=0, i =1,2,.n g dt g这就是著名的拉格朗日方程，这里L称为拉格朗日函数，它由动能L=T-UT和位能U组成（1411）泛函式的极值条件又可以写成b(T -U)dt

27、=0a(1412)这就是哈密顿原理。具有n个质点的质量为 的函数，它们之间的关系为m的力系，各质点上作用的力为 Fi （又称力函数），是位能uFx-UFyFz=(1413)这个力系的动能T为T 丄 my22心于是泛函式为口 = Ldt =( (T U)dt = ( 2瓦 m(Xi + yi + zJU dtt1t1根据式（1.4.10）,并利用式（1.4.13），得拉式方程为同理.:L d jL二 0次 dt BXi?L r(T-U) :Uex纠d；:Ld；:Tdtxdt- xc xic xim yi-Fy= Fx|* 1d m xi = m dtIXIi=1,2.nm zi - Fz例4薄板

28、弯曲振动微分方程薄板弯曲的弯矩及扭矩为-2wM x 二-D( 2dx2:w.v 2)，yMycw-2y2:w.十2 )，x2gw薄板变曲应变能为1 -u s s MD “ ；：2w （ | -.x-2:w -x亍M:X-2:-wy - 22M；：2wdxdy:xy,：2w ；：2w.r 2(l-v)():y：x：yxy)2 -(今)2 2v= byex_=2w、2动能为T二丄2能量泛函式为ti = f (T -U )dtdst0 S-：W、2-2:w 2-d(r2x2v-2- 2-2W ：- w: w 222(1-v)()2 dxdydt:x : y:x .y |?(x,y)-4:w-4y这一

29、泛函是只含有时间 t的一阶导数和x,y的两阶导数的函数，其欧拉方程直接由式（148） 得4-4ww-2- D (- 42 - 2 - 2 t；x :x ；y这就是薄板弯曲的振动微分方程式。 2.5条件极值问题上几节讨论的泛函极值问题，习惯上称为无条件极值问题。所谓无条件，并不是说在自变函数选取中不考虑任何条件。自变函数必须使给定泛函在某一范围内有意义，并满足边界条件，因为这些条件容易被满足，所以称为无条件极值问题。在工程实际中，有些约束条件 不易得到满足，这种在给定约束条件下来求泛函极值，称为条件极值问题。2.5.1函数条件极值问题求函数(2-72)2 2F (x, y) = x 2y 2xy

30、 3x 5在约束条件 Yx, y) =x y =0下的极值问题。上述极限问题有两种方法，第一种方法是由约束条件式消去y,代入(2-72)式，得y = X2F (x, y) = x 3x 5dF函数取得极值的条件是=2x+3 = 0，得 x=-3/2, y=-3/2,F(-3/2, 3/2)=11/4 .dx第二种方法是利用拉格朗日乘子法进行求解。选择拉格朗日乘子，把，乘以条件式，与式(2-72)相加，形成新的泛函F (x, y, J = x2 2y2 2xy 3x 5 (x y)(2-73)这时新的泛函 R不仅是x，y的函数，同时也是，的函数，F)的极值条件为互=2x 2y 3 =0x互二 4

31、y 2x -0：Fi_ = x y = 0上面第三式正是约束条件式。由此可解出x=-3/2, y=3/2,九=-3.把它代入式(2-73)，得F1(-3/2, 3/2, -3)=11/4，其结果与第一方法完全相同。拉格朗日乘子法是通过拉格朗日乘子，将有条件极值问题的旧函数改造成为无条件极值问题的新函数。有时把拉格朗日乘子又称为权数或权函数，这是行之有效的一种方法，加权残值法、广义变分原理也是基于拉格朗日乘子法得来的。2.5.2泛函条件极值问题约束条件式1为x,y1, y2,.yn的函数i(x,yi, y2,.yn) =0(i =1,2,.k) k n(2-74)满足式(2-74)的约束条件下，

32、求泛函XIII二二F(x,y1,y2,.,yn,y1, y2,.yn)dx(2-75)x0的条件极值问题。与前述一致，此问题也有两种方法，第一方法是通过式(2-74)的k个自变函数 来表示泛函式(2-75)中的n-k个未知自变函数。把n个未知自变函数泛函式(2-75)的有条件极值问题 转化为n-k个未知自变函数的泛函极值问题。第二种方法是拉格朗日乘子法，选择拉格朗日乘子函数i(x),i =1,2,.k，乘以式(2-74)，相加式(2-75)的函数F中，得到新的泛函 二!xiX0- nt|F +瓦入(xW/x/y,.%) dx =xiF1dxXo(2-76)(2-77)(2-78)2Fyj(xl

33、- yjd ；:Fdx :yj=0(2-79)显然，泛函二i是自变函数yj(j=1,2,.,n)的函数，同时又是=1,2,.,k)的函数，因 此泛函是n+k个未知自变函数的极值问题。 首先对式(2-76)用j求极值，即j有变分时极值 条件为二1 二:i(x,yi,y2,., yn)、idx = 0 i =1,2,.,kx0因为、是任意值，不等于零，上式可导出i(x, %2，.%) =0 (i =1,2,., k)这就是约束条件式(2-74)下求泛函式(2-75)的极值问题。不难证明，式(2-76)的欧拉方程为(2-80)为了能求出待定拉氏乘子 -x，需要诸乘子的系数满足下列行列式不为零的要求，

34、即:y斜2轨:2: 2找1汙2a-：Vn3;-:：2：n* -;1鋼2时：Yi同理，约束条件含一阶导数的情况，即i(x, y1,y2,.yn,y1,兀,yn) =0i = 1,2,., k; n k(2-81)求泛函(2-82)口 = f F(x,y1,y2,.,yn,y1,y2,.yn)dxx的极值问题欧拉方程为：Yjn: (x) i廿:y1i(x)j =1, 2,n.(2-83)在式(2-81)的约束条件下求泛函(2-84)x F(x,y1,y2,，yn, %2,.必，WM，yn)dxxo的极值问题的欧拉方程为dcF：:F J /、二+Z入（x）cyj y by dcy例1如图（1.5.1

35、）所示梁在X = l处W = w， 式。这例题相当于求泛函訂ElJwh(a)在x=l处约束条件为二W_w=o时的 图1.5.1极值条件。用拉格朗日乘子 ，建 立新的泛函d2 /汗、门+ 丁2（）= 0 j =1, 2,n.（2-85）:y jdx :y jw为给定端点挠度，建立欧拉方程及边界条件口1 = fEI (耸)2 -1012dx2 (w- w) l(b)其变分式为d2wd2、w1El 222 dx2 dx2对上式右第一项进行两次分部积分，得二 1 qw dx +)3w J +6k(w W) l(c)l ei d2 w d wd222 dx 阳噢业 0-3(学Z00笙(El 琴)、wdx

36、 (d)dx2 dx2dx2 dx dx dx20dx2dx2把上式代入式(c),并整理后，其极值条件为l d2d2wJ02(EIf)-01| dxdxEl dx上式成立的条件为w |d2w dw ldx2 dx 02 .El w 0 (w_w) = 0dx dx(e)(1)咅(EI%W0在x=ol域内(2)(El ? ) - 0或 w - 0 dxdx2在x:=l处(3)w - w = 0在x =：l处(4)(El 2 ) - 0或 w - 0在x=0处2.2(f)肾0或dx在x=0处和在x= l处例2证明如图1.5.2的无条件泛函式为讣 2Ei(dXW)2-qwdx+吶-e|3ddxW)1

37、.2d w 小2 0。dx2(g)上式中第一式是梁弯曲微分方程式， 即欧拉方程；第二式是确定拉格朗日乘子的方程， 很明 显，拉格朗日乘子的物理意义是在 x = l处的剪力；第三式就是给定约束条件；第 4和第5 式是剩余的边界条件，其中包括基本边界条件 ：?w = o和d =0以及自然边界条件，即弯dx矩、剪力的边界条件，如图1.5.1的情况，在x=0处W = 土巴=0，在x = 1处EIdx由式(f)的第二式，把.代入式(b)得新的泛函式1 d2w 2. dd2w二1 = EI( 2)-qwdx (EI牙)(w-w)i0 ：2dx- dx dx由此可知，泛函极值方程(e)给出欧拉方程式和所有边

38、界条件式，所以变分问题式(c)等价于式(f)的微分方程的解。T1.5.22.6加权残值法大量的应用科学和工程学问题往往可以归结为根据一定的边界条件，初始条件等，来求解问题的控制微分方程式或微分方程组或关键的积分方程。微分方程式(组)可以是常微分方程，偏微分方程，线性的或非线性的。加权残值法是一种数学方法，可以直接从微分方程 式(组)中得出近似解。该方法用于解算力学问题具有原理的统一性和方法的一致收敛性， 应用的广泛性，且简便，准确，工作量少，程序简短，亦可用于解复杂问题等优点。2.6.1加权残值法的基本方法按权函数进行分类，加权残值法共有五类，可称为加权残值法的基本方法。1、最小二乘法解某一问

39、题时，在物体域 V内的残值R平方积分式为：I (C j)二 R2dv(2-86)JLv为使l(Cj)为最小，应用求函数的极值条件：l c0(2-87)-Cj可得消除残值方程式为：R dv=0(j=1,2,n)(2-88)v ；Cj式，足以求出n个待定系数；Cj (j=1,2,n)。如果求解的问题系属二维的，则有最小二乘法消除残值方程组为:R(x, y)：R,y)dA = 0(j,k=1,2,n)ACjk(2-89)同样，三维问题的最小二乘法消除残值方程组为:cR(x, y, z)i i iR(x, y,z)dv=0(j,k,l=1,2,n)vCjkl(2-90)2、配置法最初发展的配置法仅是配

40、点法，今年来在我国发展了配线法， 配面法及配域法等， 这里将详述配点法。这是一种使用极为广泛又很方便的加权残值法。如果以笛拉克函数作为权函数：Wj = (x _ Xj)(2-91)就得到了配点法。笛拉克函数又称为单位脉冲函数。 一维的单位脉冲函数其主要的性质如下：a.址切屮(X=Xj) j 10, (x 鼻 Xj)(2-92)b.oa(x _xjdx =1(2-93)c.c 11, 、(x _Xj )dx 二 a 0,(a ： xj : b)(x ： a,或x b)(2-94).丈f(xj),i f(x)咅(x-Xj)dx=xA3x.(1一 2)(1- 2) .(2-113)aa5、双B样条函

41、数 形式如：二二 rj i(x) )(y)(2-114)i ji(x)及j (y)都是B样条函数，从3次到9次。6、多项式与三角函数积并与多项式之和形式如：2 2G C2rC3r cosC4rsin) .r sinvcosv (2-115)7、双调和函数如由 esin Py,coy,xesin By,yy coH.组成，或为：G cos： /ch “y C2 cos 2xsh2y C3sin: 3xch 3y .(2-116)8、梁振动函数GmS in mX C2mC0SmX CsmShmX C4mChmX(2-117)9、对数函数rr女口：C1 C2r2 ln r2 ln , In(i =1

42、,2,3,.),.(2-118)aai用于分析开孔物体中。10、指数函数如：Aeir,尹如 .11、贝塞耳函数女口： AJo() BJ() .12、“完备系”试函数女口： C1 C2r2. rn(cosn： sinn)13、柱稳定函数女口： C1 C2x sink：x cosk二 x试函数是选择在低级近似计算中十分重要。因为，这会影响计算结果。在高级近似计算中则不太重要，因为，计算中依靠了解的收敛性。试函数选择得当与否只会影响解的收敛速度。试函数必须是完备的并且各试函数项之间是线性无关。属于连续的函数大多可以用多项式展开。试函数的完备性能够保证在取足够多的试函数项时可以逼近精确解，所以比较重要

43、。拟解决问题的对称性和边界条件可以帮助确定试函数的形式。对称问题，试函数也应该是对称的。如果已知一个问题中的边界条件为g(x,y)，则这问题中的试函数可假设为：_nu(x,y)二 g(x,y) GNj(x,y)(2-119)i =1当然，式中试函数项 M在边界条件上应为零。多种正交多项式都是有用的试函数。它们可以满足若干边界条件，再附加一定的多项式以满足其他的边界条件。 这种设立试函数的方法可以满足一些难以全部满足边界条件的边值 问题，如大挠度板壳及厚板厚壳问题。正交多项式的正交性可以使得计算正确方便。超越函数可以作为试函数，但大多用作初次近似的试函数，在高次近似计算中，则有计算累赘不堪的缺点

44、。这类函数可以作为特征值问题的试函数。有限元法单元中，位移模式所用的试函数也可以作为加权残值法的试函数。各类样条函数都可以作为加权残值法的试函数。2.7 Ritz 法和 Galerkin 法2.7.1基于位移变分原理的Ritz法使用位移变分原理求解，首先需要列出所有变形可能的位移，然后从中找出使总势能取驻值的那组位移，这就是真实位移。对于稳定平衡状态，相应于位移变分原理的最小势能原 理成立，因此使总势能取最小值的那组位移，就是真实位移。但问题在于要列出所有变形可能的位移非常困难，也不现实。因此，在求解实际工程问题时，只能根据受力特点和边界条 件，凭经验假设一组位移的实验函数，其中包括有限个待定

45、常数，这种处理缩小了寻找位移解的范围。若从中找出一组使总势能取最小值的位移，一般来说，这组位移不是真正的位移，但它在缩小的范围内是与真实位移最接近，从而可以作为问题的近似解。设位移实验函数为：nUx 三 Uxo akUxk(x, y,z)kz1nUy 三 Uyo bkUyk(x,y,z)(2-120)nUz 二 Uz0 CkUzk(x, y,z)k 式中Ux0、Uy0、Uz0和Uxk、Uyk、Uzk是预先设定的空间坐标的函数，Uxk、Uyk、gk称为基函数或形状函数(它表示变形形状)，应当满足函数连续性、可微性、线性独立性及基本边界条件(又称固定边界条件，但自然边界条件不一定必须满足)，基函数是选择函数，一般采用指数函数或三角函数，此时函数的连续性、可微性及独立性易被满足，所以选择基函数时特别注意满足边界条件。而ak、bk、Ck是待定系数又称广义参数，由泛函极值条件确定。位移的变分是通过待定系数a、bk、ck取变分来实现的，而与函数uxk、uyk、uzk无关，于是：n、UxakUxk(x, y,z)k =1n、Uy 八bkUyk(x,y,z)(2-121)k =nuCkUzk(x,y,z)k斗位移实验函数必须满足位移边界条件，且