计算方法拉格朗日插值

《计算方法拉格朗日插值》由会员分享，可在线阅读，更多相关《计算方法拉格朗日插值（5页珍藏版）》请在装配图网上搜索。

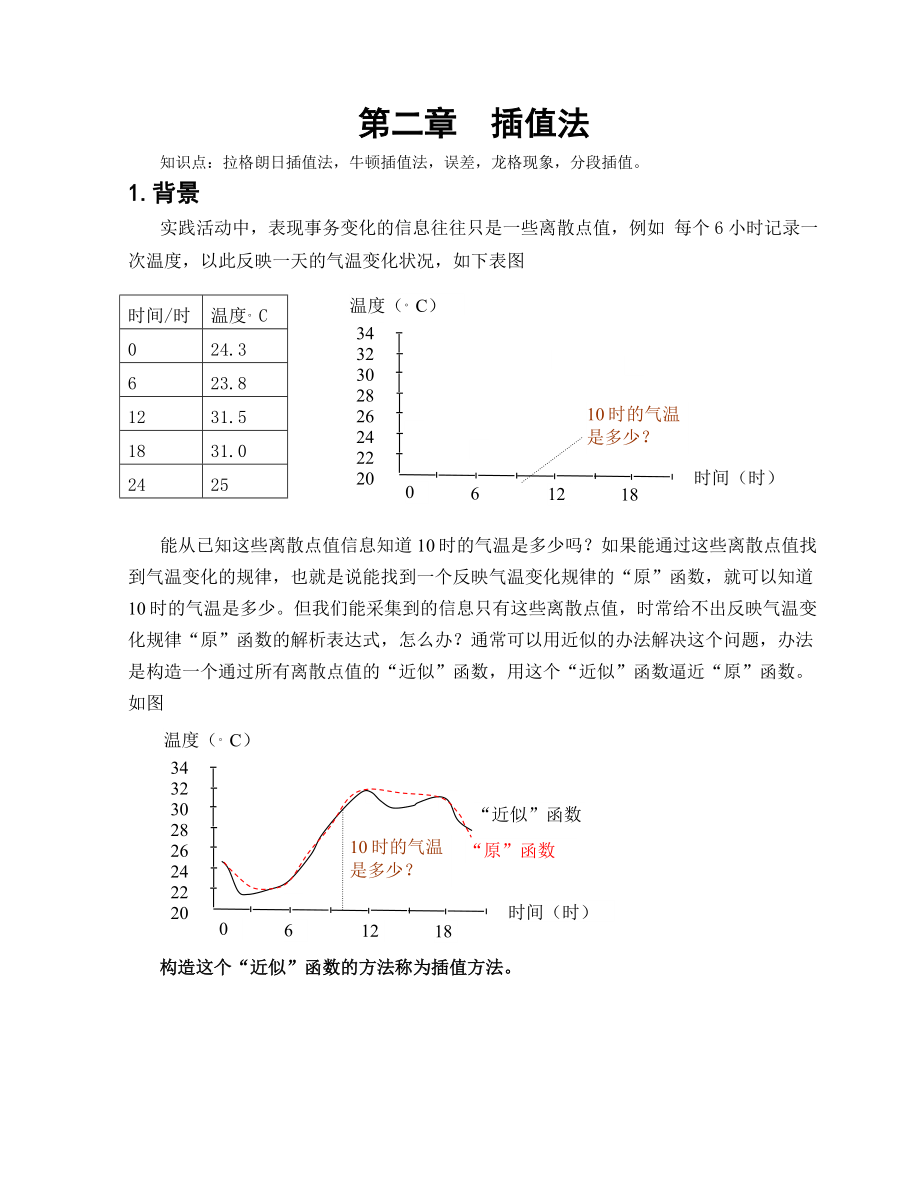
1、第二章 插值法知识点：拉格朗日插值法，牛顿插值法，误差，龙格现象，分段插值。1.背景实践活动中，表现事务变化的信息往往只是一些离散点值，例如 每个6小时记录一次温度，以此反映一天的气温变化状况，如下表图时间/时温度。C024.3623.81231.51831.024253432302826242220时间（时）温度（。C）06121810时的气温是多少？能从已知这些离散点值信息知道10时的气温是多少吗？如果能通过这些离散点值找到气温变化的规律，也就是说能找到一个反映气温变化规律的“原”函数，就可以知道10时的气温是多少。但我们能采集到的信息只有这些离散点值，时常给不出反映气温变化规律“原”函数

2、的解析表达式，怎么办？通常可以用近似的办法解决这个问题，办法是构造一个通过所有离散点值的“近似”函数，用这个“近似”函数逼近“原”函数。如图3432302826242220时间（时）温度（。C）10时的气温是多少？“近似”函数“原”函数061218构造这个“近似”函数的方法称为插值方法。2.概念实际问题中，能采集到的信息只是一些离散点值xi,f(xi)(i=0,1,2,n)，时常给不出一个函数f（x）的解析表达式，因之，转而考虑选择一个简单的函数j（x）近似替代（原来）f（x）。定义：设f（x）为定义在区间a，b上的函数，x0,x1,xn为a，b上的互异点，yi=f（xi）。若存在一个简单函数

3、j（x），满足（插值条件）j（xi）=f（xi），i=0，1，n。则称 j（x）为f（x）插值函数，f（x）为被插函数,点x0,x1,xn为插值节点,点xi,f(xi),i=0,1,2,n为插值点。若用j（x）f（x），则计算f（x）就转换为计算 j（x）。插值需要解决：插值函数是否存在唯一；插值函数如何构造；插值函数与被插函数的误差估计和收敛性。对插值函数的类型有多种不同的选择，代数多项式pn(x)常被选作插值函数 j（x）。P23(2.18)和(2.19)指出，存在唯一的满足插值条件的n次插值多项式pn(x)。但是需要计算范德蒙行列式，构造插值多项式工作量过大，简单表达式不易得到，实际中不

4、采用这类方法。pn(x)(x)被插函数： (x)j(x)=pn(x)：插值函数M0M1Mn拉格朗日（Lagrange）、牛顿（Newton）等分别给出了不同的解决方法。3拉格朗日插值插值法是一种古老的数学方法，拉格朗日（Lagrange）插值的基本思想是把插值多项式pn(x)的构造问题转化为对n+1个插值基函数li(x)(i=0,1,n)的构造。(1)线性插值构造插值函数已知函数y=f(x)的两个插值点(x0,y0)，(x1,y1)，构造多项式y=p1(x)，使p1(x0)=y0,p1(x1)=y1。由直线两点式可知，通过A，B的直线方程为BAx1y=f(x)y=p1(x)x0y1y0则p1(

5、x)=l0(x)y0+l1(x)y1f(x)，满足：l0(x0)=l1(x1)=1，l0(x1)=l1(x0)=0，p1(x0)=y0，p1(x1)=y1。插值完毕！这种插值方法称作为拉格朗日插值，l0(x)，l1(x)称为点x0、x1的线性插值基函数，插值函数p1(x)是这两个插值基函数的线性组合，相应的多项式称拉格朗日线性插值多项式，记作L1（x），即L1（x）f(x)。误差设L1（x）为插值点(x0,y0)，(x1,y1)的插值函数,f(x0)=y0,f(x1)=y1,f(x)一阶连续可导,二阶导数存在.则对任意给定的xa,b,存在一点a,b,使引进辅助函数,利用洛尔定理即证，见P17定

6、理2.1。(2)二次插值构造插值函数给定三个点xi,f(xi),i=0,1,2,其中xi互不相同，构造函数f（x）的二次插值多项式L2（x），满足：L 2(x0)=y0,L2(x1)=y1,L2(x2)=y2。通过三点的插值问题称为二次插值或抛物插值。仿线性插值，用插值基函数构造插值多项式。x0x1x2y2=f(x2)L2(x)f(x)y1=f(x1)y0=f(x0)令L2（x）=l0(x)y0+l1(x)y1+l2(x)y2待定函数li(x)应是二次函数，满足约束条件li(xi)=1，li(xj)=0（ij），i，j=0，1，2。此设l0(x)=A(x-x1)(x-x2)，l1(x)=B(x

7、-x0)(x-x2)，l2(x)=C(x-x0)(x-x1)。根据约束条件确定系数由此得误差证明见P22定理2.2。(3)一般情况两个插值点可求出一次插值多项式L1(x)，而三个插值点可求出二次插值多项式L2(x)。当插值点增加到n+1个时，利用Lagrange插值方法写出n次插值多项式Ln(x)。详细说明见P22-24，（2.20），（2.21）至（2.24）。(4) 例子设sin11=0.190809，sin12=0.207912，sin13=0.224951，计算sin1130。解：（1）线性插值计算插值：L1(11.5)=0.199361sin1130误差（2）二次插值计算L2(11.5)=0.199369.(5)关于Langrange插值的几点说明Ln(x)仅与已知数据(xi,yi),(i =0,1,n)有关，与f(x)的原来形式无关，但余式与f(x)密切相关。若f(x)本身是一个不超过n次多项式，则Rn(x)=0,即Ln(x)f(x).内插（x位于x0,x1,xn之间）误差较小，外插有可能误差变大，慎用!插值点的增减,基函数要重新计算,很不方便!插值节点过多其精度不一定很好；limLn(x)=f(x)(xa,b)一般不成立.