清华 运筹学(课堂PPT)

《清华 运筹学(课堂PPT)》由会员分享，可在线阅读，更多相关《清华 运筹学(课堂PPT)（45页珍藏版）》请在装配图网上搜索。

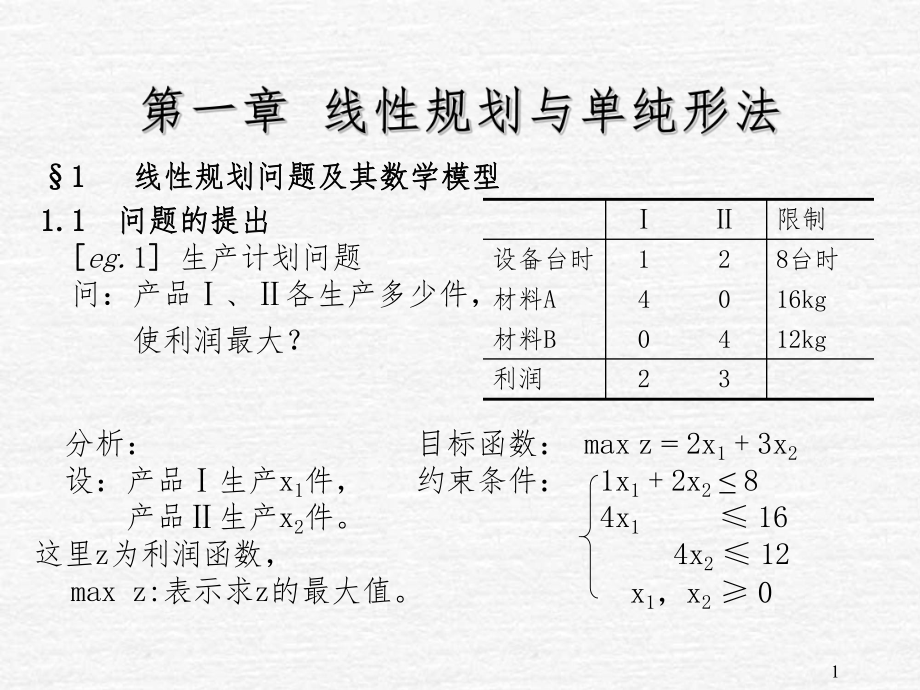
1、11 1 线性规划问题及其数学模型线性规划问题及其数学模型1.1 1.1 问题的提出问题的提出 eg.1 生产计划问题 问：产品、各生产多少件，使利润最大？限制 设备台时128台时 材料A4016kg材料B0412kg利润23 分析：设：产品生产x1件，产品生产x2件。这里z为利润函数，max z:表示求z的最大值。目标函数：max z=2x1+3x2约束条件：1x1+2x2 8 4x1 16 4x2 12 x1，x2 0 2 eg.2 污水处理问题 环保要求河水含污低于2，河水可自身净化20%。问：化工厂1、2每天各处理多少污水，使总费用最少？分析：化工厂1处理污水x1万m3,化工厂2处理污

2、水x2万m3。min z=1000 x1+800 x2 (2-x1)/500 2/1000 (1-0.2)(2-x1)+1.4-x2/(500+200)2/1000 x1 2 x2 1.4 x1，x2 0 这里min z:表示求z的最小值。200万m3500万m32万m31.4万m3化工厂1化工厂21000元/万m3800元/万m33线性规划的数学模型：线性规划的数学模型：max(min)z=c1x1+c2x2+cnxn a11x1+a12x2+a1nxn(=,)b1 a21x1+a22x2+a2nxn(=,)b2 am1x1+am2x2+amnxn(=,)bm x1，x2，xn 04说明：(

3、1)决策变量：x1，x2，xn。一组决策变量表示为问题的一个方案；(2)目标函数：max(min)z z为决策变量的线性函数;(3)约束条件 一组线性不等式。cj为价值系数,bi为资源，aij为技术系数(i=1,m;j=1,n).51.2 1.2 图解法图解法 eg.eg.33用图解法求用图解法求eg.eg.1 1。max max z z=2x2x1 1+3x3x2 2 1x 1x1 1+2x2x2 2 8 8 4x 4x1 1 16 16 4x4x2 2 12 12 x x1 1，x x2 2 0 0 解：(1)建立x x1 1-x x2 2坐标；x2x1 (2)约束条件的几何表示；Q1Q2

4、Q3Q4 (3)目标函数的几何表示；*z z=2x2x1 1+3x3x2 2 o43zxx3132126 首先取z=0，然后，使z逐渐增大，直至找到最优解所对应的点。*可见，在Q2点z取到最大值。因此，Q2点所对应的解为最优解。Q2点坐标为(4，2)。即:x1=4，x2=2 由此求得最优解：x x1 1*=4 x4 x2 2*=2 2 最大值：maxmax z z=z z*=2x2x1 1+3x3x2 2=14(14(元元)x2x1Q1Q2(4,2)Q3Q4*437讨论：(1)唯一最优解 maxmax z z =z z*时，解唯一，如上例。(2)无穷多最优解 eg.4 对eg.1，若目标函数

5、z z=2x2x1 1+4x4x2 2，此时表示 目标函数的直线与表示 条件的直线平行，最优点在线段Q3Q2上。即存在无穷多最优解。x2x1Q1 Q2(4,2)Q3(2,3)Q4o43*8 (3)无界解 eg.5 max z=2x1+3x2 4x1 16 x1，x2 0 则x2 ，z 。即存在无界解。在实际问题中，可能 是缺少约束条件。o2241x2x9(4)无可行解 eg.6 max z=2x1+3x2 2x1+4x2 8 x1+x2 1 x1，x2 0 无公共部分，无可行域。即无可行解。在实际问题中，可能是关系错。1124x1x2101.3 1.3 线性规划的标准型线性规划的标准型 1、标

6、准型 max z=c1x1+c2x2+cnxn a11x1+a12x2+a1nxn=b1 a21x1+a22x2+a2nxn=b2 am1x1+am2x2+amnxn=bm x1，x2，xn 0 njxmibxaxczjinjjijnjjj,10,1 max11 ，简记：11用向量表示 njxbxptsCXzjnjjj,1,0 .max1TmjTmjjjjnTnbbbbxaaapcccCxxxX)(:)()()(:21212121 的系数列向量其中12 用矩阵描述为：max z=CX AX=b X 0 其中:X=(x1,x2,xn)T C=(c1,c2,cn)b=(b1,b2,bm)T 为系数

7、矩阵 212222111211 mnmmnnaaaaaaaaaA132 2、标准型的化法标准型的化法 (1)(1)minmax min zminmax min z=cxcx=-max(-z)-max(-z)max(-z)max(-z)=-min z-min z=-cx-cx 令令zz=-z -z 则则max zmax z=-cx-cx (2)(2)不等式不等式(，)对于对于“”情况：在情况：在“”左边加上一个松弛变量（非左边加上一个松弛变量（非负）负），变为等式；变为等式；对于对于“”情况：在情况：在“”左边减去一个剩余变量（非左边减去一个剩余变量（非负），变为等式。负），变为等式。注意：松弛

8、变量、剩余变量在目标函数中的价值系数为注意：松弛变量、剩余变量在目标函数中的价值系数为0 0。(3)(3)无约束变量无约束变量 令令x xk k=x xk k-x xk k”，x xk k,x,xk k”0 0，代入即可。代入即可。14 eg.eg.77将下述问题化为标准型将下述问题化为标准型 min zmin z=-x-x1 1+2x+2x2 2-3x-3x3 3 x x1 1+x+x2 2+x+x3 3 7 7 x x1 1-x-x2 2+x+x3 3 2 2 -3x-3x1 1+x+x2 2+2x+2x3 3=5 5 x x1 1,x,x2 2 0 0，x x3 3无约束无约束 解：令解

9、：令x x3 3=x x3 3-x-x3 3”，x x3 3,x,x3 3”0 0；式加上一个松弛变量式加上一个松弛变量x x4 4；式减去一个剩余变量式减去一个剩余变量x x5 5；令令z z=-z-z max zmax z=x x1 1-2x2x2 2+3(x3(x3 3-x x3 3”)+0 x0 x4 4+0 x0 x5 5 x x1 1+x x2 2+(x+(x3 3-x x3 3”)+x x4 4 =7 7 x x1 1-x x2 2+(x+(x3 3-x x3 3”)-x x5 5=2 2 -3x -3x1 1+x x2 2+2(x2(x3 3-x x3 3”)=5 5 x x1

10、 1,x,x2 2,x,x3 3,x,x3 3”,x,x4 4,x,x5 5 0 0 151.4 1.4 线性规划解的概念线性规划解的概念 设线性规划为 maxmax z z=CX CX AX AX=b b X X 0 0 A A为为m m n n矩阵矩阵,n n m,Rankm,Rank A A=m(Am(A为行满秩矩阵）为行满秩矩阵）1 1、可行解：满足条件、可行解：满足条件、的的X X；2 2、最优解：满足条件的可行解；、最优解：满足条件的可行解；3 3、基：取、基：取B B为为A A中的中的m m m m子矩阵，子矩阵，RankRank B B=m m，则称则称B B为线性为线性规规

11、划问题的一个基。划问题的一个基。取取B B=(p(p1 1,p,p2 2,p,pm m)p)pj j=(a(a1j1j,a,a2j2j,a,amjmj)T T 则称则称x x1 1,x,x2 2,x,xm m为基变量，其它为非基变量。为基变量，其它为非基变量。164 4、基解：取、基解：取B B=(p(p1 1,p,p2 2,p,pm m)a a1111,a,a1m1m x x1 1 a a1m+11m+1,a,a1n1n x xm+1m+1 b b1 1 +=a am1m1,a,ammmm x xm m a amm+1mm+1,a,amnmn x xn n b bm m 基基 基变量基变量

12、非基非基 非基变量非基变量 令令 x xm+1m+1=x xn n=0(0(非基变量为非基变量为0)0)则则 BXBXB B=b b )!(!mnmnCmn基解个数TmnmTmBxxxXxxxbBX)0,0,(),(m)0()0(2)0(1)0()0(2)0(11 个个基解：175、基可行解 满足式要求的基解。如右图所示，各边交点O,QO,Q1 1,Q,Q2 2,Q,Q3 3,Q,Q4 4均为基可行解；而其延长线的交点Q5为基解，但不是基可行解。O(0,0)O(0,0)Q Q1 1(4,0)(4,0)Q Q2 2(4,2)(4,2)Q Q4 4(0,3)(0,3)Q Q3 3(2,3)(2,3

13、)Q Q5 5(4,3)(4,3)6、可行基 基可行解对应的B为可行基。可行解可行解基可行解基可行解非可行解非可行解基解基解182 2 线性规划问题的几何意义线性规划问题的几何意义2.1 2.1 基本概念基本概念 1 1、凸集：设、凸集：设K K为为E En n(n(n维欧式空间维欧式空间)的一点集，的一点集，X X(1)(1)K K，X X(2)(2)K K。若若XX(1)(1)+(1-)X+(1-)X(2)(2)K K，则称则称K K为凸集。（为凸集。（0 01 1）非凸集X X(1)(1)X X(1)(1)X X(2)(2)X X(2)(2)凸集X X(1)(1)X X(2)(2)X X

14、(2)(2)X X(1)(1)19 2 2、顶点：、顶点：X XK K，X X(1)(1)K K，X X(2)(2)K(K(任意两点任意两点)。若。若X X不能用不能用XX(1)(1)+(1-)X+(1-)X(2)(2)表示，则称表示，则称X X为为K K的一个顶点。的一个顶点。(0(01)1)注：顶点所对应的解是基可行解。注：顶点所对应的解是基可行解。3 3、凸组合：设、凸组合：设X X(i)(i)E En n，若存在若存在0 0i i1 1，i i=1,2,1,2,k,k，使使 ,则称则称X X为为X X(i)(i)(i=1,2,(i=1,2,k),k)的凸组合。的凸组合。1k1iik1i

15、)i(iXX2.2 2.2 基本定理基本定理 1 1、定理、定理1 1 若线性规划存在可行域，则若线性规划存在可行域，则:可行域可行域 D D=X|AXX|AX=b,Xb,X 00为凸集。为凸集。20 证明：证明：设设 X X(1)(1)=(=(x1 1(1)(1),x2 2(1)(1),xn n(1)(1)T T D D；X X(2)(2)=(=(x1(2)(2),x2 2(2)(2),xn n(2)(2)T T D D；(X (X(1)(1)X X(2)(2)有有 AXAX(1)(1)=b b，AX AX(2)(2)=b b 令令 X X=XX(1)(1)+(1(1-)X)X(2)(2)(

16、0(0 0 10 1 0 0 X X 0 0，即即D D为凸集为凸集 2、定理2 线性规划的基可行解对应于可行域的顶点。3、定理3 若线性规划有解，则一定存在基可行解为最优解。213 3 单纯形法单纯形法 基本思路：基本思路：从可行域的一个顶点到另一个顶点迭代求最优解。3.1 3.1 初始基可行解的确定初始基可行解的确定 1、松弛基（松弛变量对应的B）eg.8 max z=x1+3x2 x1+2x2 3 2x1+3x2 4 x1,x2 0max z=x1+3x2+0 x3+0 x4 x1+2x2+x3 =3 2x1+3x2 +x4=4 x1,x2,x3,x4 0 化标准型 取x3、x4为基变量

17、,令非基变量x1=x2=0 初始基可行解：X(0)=(0 0 3 4)T B ,1 0 3 20 1 2 1 434321ppppppA则系数矩阵22 2、观察法 eg.9 max z=x1+3x2+2x3+x4 x1+2x2+3x3 =3 3x2+x3+x4=4 x1,x2,x3,x4 0 选 XB=(x1 x4)T 令x2=x3=0 则 初始基可行解：X(0)=(3 0 0 4)T B ,1 1 3 00 3 2 1 :414321ppppppA则解233、人工基 eg.10 max z=x1+2x2+3x3 x1+3x2+2x3=3 2x1+x2+x3=4 x1,x2,x3 0 分析：A

18、=1 3 2 2 1 1 找不到单位矩阵基 引入人工变量为初始基变量（2个）243.2 3.2 最优性的检验与解的判别最优性的检验与解的判别 mnjxmibxxaxcxczjnjiinjijmiininnjjj,1 0,1 max 111对于代入目标函数为非基变量可行为基变量设 ,1,1,1 njjijiinjinxabxnjxmix25则njjjnjjjjnjmijijinjmiiinnjminjjijiinjjxZxzcZxaccbcxabcxcz1010111111 )()()(miijinjjjjmiiinaczzcbcZ110 ,其中26解的判别：1.若 ，则此时的基可行解为最优解；

19、2.若存在某个非基变量 的检验数 ，且 ，则该线性规划问题具有无界解（或称无最优解）；3.若所有 ，又，对于某个非基变量 有 ，则该线性规划问题具有无穷多最优解。.的检验数为称jjxkx0knjj,1,0 0kp0j0kkx27 为主元出基行对应的变量则若、出基变量 0minmin02lkllklikikiiiiikikiiaxlabaabaab为入基变量。则，若、入基变量kkjjx 0max13.3 3.3 基变换基变换283.4 3.4 旋转运算（消元运算）旋转运算（消元运算）a1k 0 al-1k 0 pk=（alk）（1）al+1k 0 amk 0 得到基可行解，重复3.23.4，求出

20、最优解。293.5 3.5 单纯形表单纯形表 展开如下：a11x1+a12x2+a1nxn+xn+1 =b1 -cn+1 a21x1+a22x2+a2nxn +xn+2 =b2 -cn+2 am1x1+am2x2+amnxn +xn+m =bm -cn+m c1x1+c2x2+cnxn+cn+1xn+1+cn+mxn+m-z=0 1x1+2x2+nxn+0 xn+1 +0 xn+m-z=Z0mn,2,1j0 xbxxaxczmaxjiinn1jjijmn1jjj，设30 建立单纯形表cBxBbc1cncn+1cn+mx1xnxn+1xn+mcn+1xn+1b1a11a1n101cn+mxn+m

21、bmam1amn01m -z -z01 n 00j eg.11 用单纯形法求解 max z=x1+3x2 x1+2x2 8 4x1 16 4x2 12 x1,x2 031 解：标准化，建立单纯形表 引入松弛变量x3，x4，x5为初始基变量 max z=x1+3x2+0 x3+0 x4+0 x5 x1+2x2+x3 =8 4x1 +x4 =16 4x2 +x5=12 x1,x2,x3,x4,x5 0cBxBbx1x2x3x4x5 13000cBxBbx1x2x3x4x5 0 x38121000 x416400100 x51204001此时的解：x(0)=(0 0 8 16 12)Tz(0)=03

22、2 解的判别 1=1 2=3 0 x(0)非最优解 基变换 max1,2=3=2 x2入基 min8/2,-,12/4=12/4 x5出基13000cBxBbx1x2x3x4x5 0 x38121000 x416400100 x5120400113000cBxBbx1x2x3x4x5 0 x38121008/20 x41640010-0 x5120400112/41300033此时的解：x(1)=(0 3 2 16 0)Tz(1)=9x(1)非最优x1入基 x3出基0 x321010-1/22/10 x4164001016/43x2301001/4-1000-3/41x121010-1/20

23、x4800-4123x2301001/400-10-1/413000此时的解：x(2)=(2 3 0 8 0)Tz(2)=11x(2)为最优解 即：最优解：x*=(2 3 0 8 0)T 最大值：z*=1134X(0)=(0 0 8 16 12)T O(0,0)X(1)=(0 3 2 16 0)T Q4(0,3)X(2)=(2 3 0 8 0)T Q3(2,3)x2x1Q1Q2(4,2)Q3(2,3)Q4*O(0,0)354 4 单纯形法的进一步讨论单纯形法的进一步讨论4.1 4.1 人工变量法人工变量法 1、大M法（M为很大的正数）法则：对于max问题，人工变量在目标函数中的价值系数为-M；

24、对于min问题，人工变量在目标函数中的价值系数为M。eg.12 min z=x1+5x2+0 x3+0 x4 2x1+3x2+x3 =6 2x1+x2 x4 =1 x1,x2,x3,x4 0 解：min z=x1+5x2+0 x3+0 x4+Mx5 ：x5为人工变量 2x1+3x2+x3 =6 2x1+x2 x4 +x5=1 x1,x2,x3,x4,x5 0 列单纯形表求解。36min z=x1+5x2+0 x3+0 x4+Mx5 2x1+3x2+x3 =6 2x1+x2 x4 +x5=1 x1,x2,x3,x4,x5 0对于min问题，若 minj0中，选下标小的非基变量入基；对相同的最小比值，选下标小的基变量出基。.,2,10,minmin3得问题的最优解时数满足当所有非基变量的检验问题对于问题最优解的判别、njzcjjj第二章j与i的计算同max问题。45习题P45，1.4分别用图解法和单纯形法求解下列线性规划,并指出单纯形法迭代的每一步相当于图形上的哪一个顶点？0,24261553 2max)1(21212121xxxxxxxxz0,18231224 52max)2(21212121xxxxxxxxz