统计学第5-6章正态分布、统计量及其抽样分布详解

《统计学第5-6章正态分布、统计量及其抽样分布详解》由会员分享，可在线阅读，更多相关《统计学第5-6章正态分布、统计量及其抽样分布详解（20页珍藏版）》请在装配图网上搜索。

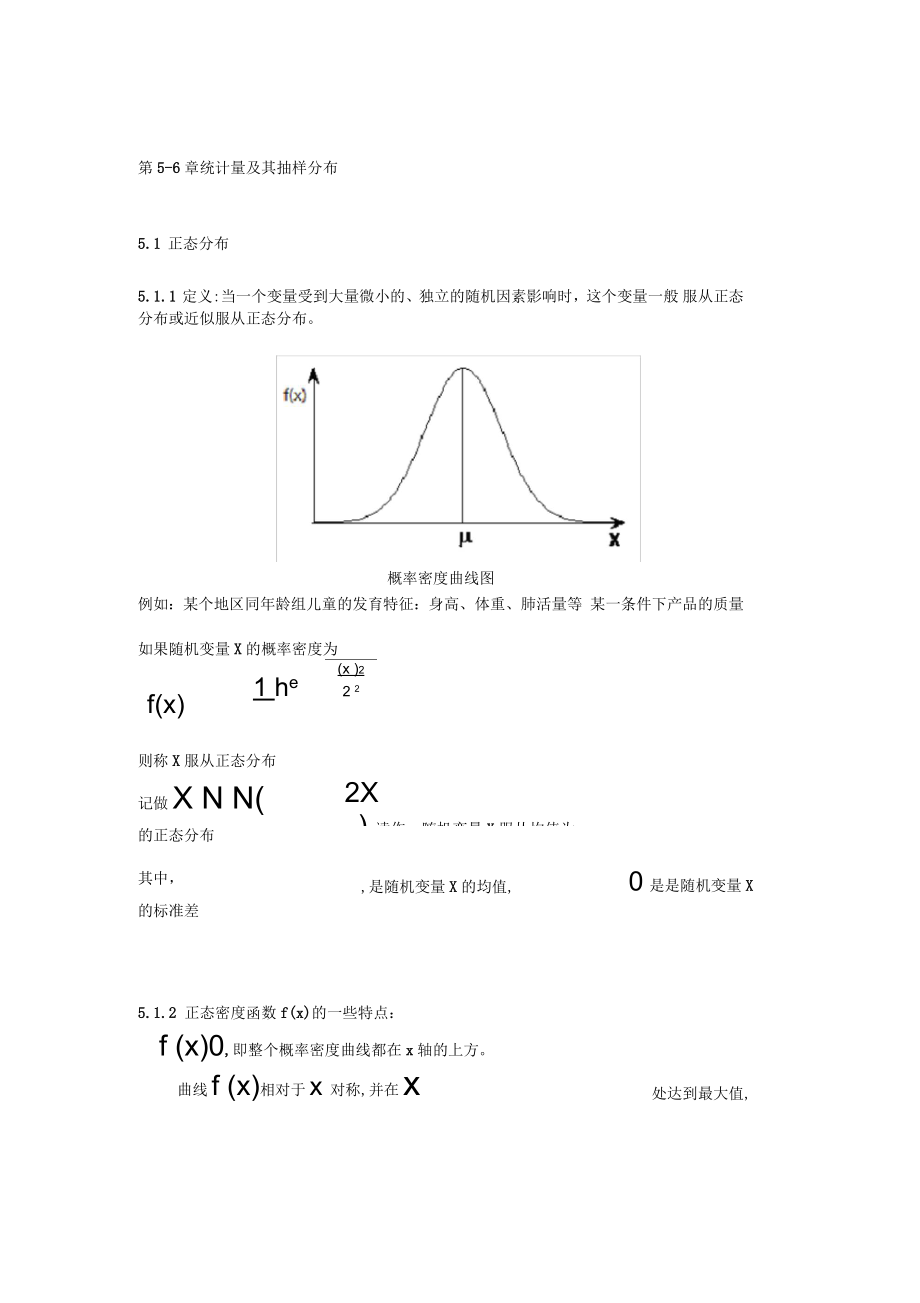
1、第5-6章统计量及其抽样分布 5.1 正态分布 5.1.1 定义:当一个变量受到大量微小的、独立的随机因素影响时，这个变量一般 服从正态分布或近似服从正态分布。 概率密度曲线图 例如：某个地区同年龄组儿童的发育特征：身高、体重、肺活量等 某一条件下产品的质量 如果随机变量X的概率密度为 f(x) 1 he (x )2 2 2 则称X服从正态分布 记做X N N( 的正态分布 其中， 的标准差 2X ),读作：随机变量X服从均值为 ,是随机变量X的均值, 0是是随机变量X 5.1.2 正态密度函数f(x)的一些

2、特点： f (x)0,即整个概率密度曲线都在x轴的上方。 曲线f (x)相对于x 对称,并在x 处达到最大值, f() o 1 <2 <3 曲线的陡缓程度由 决定： 越大，曲线越平缓; 越小，曲线越陡峭 当 X 趋于无穷时，曲线以x轴为其渐近线 标准正态分布 当 0,1时, f(x) N(0,1)为标准正态分布 标准正态分布的概率密度函数: (x) 标准正态分布的分布函数: (x) 任何一个正态分布都可以通过线性变换转化

3、为标准正态分布 设x\n( , 2)/ --Nn(0,1) 变量X N N ( 1, 12)与变量y| N( 2,；)相互独立，则有 X+Y\N( 1+ 2, 12+ I) 5.1.3 正态分布表：可以查的正态分布的概率值 (x) 1(x) 例：设 xNn(0,1),求以下概率 (1)P(X 1.5) (2) P(X2) ⑶ P( 1X3) (4)P(X 2) 解： 1.5 (1)P(X 1.5) (t)dt ⑵ P(X2)1P(X2)1 ⑶ P( 1X3)P(X3)P(X (3) (1(1)) 0.9987 (1 P(X| 2) P( 2 X 2) ⑷(2)

4、(1(2)) 2 ⑵ 一般,若x n n (0,1),则有 P(a X b) (b) P(|x|a) 2 (a) 1 例设xNn(5,32) (3)P(2 X (4) P( 6) (1.5) 0.9332 (2) 1 0.9773 0.0227 1) (3) ( 1) 0.8413) 0.84 (2) ( 2) 1 0.9545 (a) ,求以下概率 (D P(X 10) ⑵ P(2 X 10) (5)P(X 5 9) 解：由 X^ N(5,32), ^3^N N(0,1) (1) X P(X 10) P(二 10 5 3 P(1 1.67) 1.67

5、 (t)dt (1.67) 0.9522 P(2 X 10) P(2 3 10 5 3 X 5 P( 1 1.67) ⑵3 (1.67)( 1) 0.7938 5) (3) P(2 X 8) P(2-^ X 5 “、 P( 1 1) 3 2 (1) 1 2 0.8413 1 0.6826 2) P(X 5 6) P( 1 0.9544 3) P( 2 (2) 1 2 0.9772 (4) X 5 P( X 5 9) P(—^― 2 (3) 1 2 0.9987 1 0.9974 一般，若X N N( , 2),则有 P(a

6、 X b)(b-)(a-) 5.1.4 3 准则 若X Nn(0,1),则有 P(|x 1) 2 (1) 1 0.6826 P(X 2) 2 (2) 1 0.9545 P(X| 3) 2 (3) 1 0.9973 0.3% 即，x的取值几乎全部集中在3,3区间内，超出这个范围的可能不到 P(X 至一般正态总体，即X | N ( , 2),有 )0.6826 P(|X 2 ) 0.9545 显然p(x P(X 3 ) 0.9973 3 )的概率很小，因此可以认为x的值几乎一定落在区 问(3 ,3 )内一一统1t学的“ 3准则” 5.1.5 正态分布函数的一个

7、重要性质 设变量X|N( 1, 12), Y N( 2,分,x与y相互独立，则有 X+Y^N( 1+ 2, 12+ 22) X-Y^N( 1- 2, 12+ I) 5.1.6 求分位数Z 设X^N 0,1 P(X Z ) z (x)dx Z =-Z1. 常用的几个Z分位数：Z0.05 1.64,Zo.025 1.96 Z0.95 -1.64,Zo.975 -1.96 5.2由正态分布导出的几个重要分布 三大分布: 2,t,F分布 2 5.2.1 分布 1定义：设随机变量X1, X2j” , Xn相互独立，且 XiNN(0,1)(i

8、 1,2,|||,n) ,则它们的平方和服从自由度为 2 n的X分布。 记做，X；N 2(n) 2 . 2 X分布的密度函数图形 图形特点： 2 (D X 分布的变量值始终为正 度) 2 (4) X分布具有可加性。 若X与Y是相互独立的随机变量，X ~ x2(n) Y ~ X2(n2),则它 2 们的和服从于自由度为n1 r 的 X 分布，即 X Y - x2(ni %)。 w22 3 X 分布临界值表的使用，求得 X 分布的分位数 X分布临界值表中给出的是概率为时， P(x2 X2)2 f(X)dX x2 0.2八 3 (X) f

9、\ 0.1 -- 0，"」＞ X2x 例如，若随机变量x N 2(io), 则查小得 20.05(10) 3.94,0, 5.2.2 t 分布(student 分布) 设随机变量X,Y互相独立， X ~ N(0,1),Y-x2(n),贝 x的取值，k是自由度 )5 (10) 18.307, U随机变量 22 自由度为n的

10、t分布 X t .〜t(n) ,丫 n t分布概率密度函数图 特点： ① 关于y轴对称，与标准正态分布的密度函数的图像非常相似。 ②厚尾：当X 时，t分布的密度函数趋于0的速度要比标准正态分 布密度函数慢，所以t分布的密度函数的尾部要比 N(0,1)密度的 尾部厚些。 ③当自由度n无限增大时，t分布将趋近于标准正态分布。 所以，当n很大时，t分布可以用标准正态分布近似。记 t (n)为分 布t(n)的分位数。 在实际使用中，当n 30就近似有t (n) Z -5 0tt 5 由于t分布

11、密度曲线的对称性，可得 t (n)ti (n) 例如，若随机变量T N t(15),查表可得，to.05(15) 1.7531, 而 to.95(15)to.o5(15)1.76531 t0.05(40) 1.6839 t0.05 (45) 1.6794 Z0.951.645 可见随着自由度n的增大，t分位数与z分位数越来越接近 5.2.3 F分布 设随机变量 x与y相互独立且分别服从自由度为 m和n的 2 分布。 l X / m 则随机变量F ——服从第一自由度为 Y /n 记为 F N F (m, n) m 第二自由度为n的f分布

12、 F分布的概率密度函数的图 设随机变量f N f (m, n) F (m,n)表示分布F(m,n)的 分位数, 可以证明 F (m,n) Fi (n,m) 例如查表得 Fo.95(8,9)=3.23 则 %.。5(9,8)= =——0.31 Fo.95(8,9) 3.23 5.6小概率原理 指发生概率很小的随机事件在一次实验中几乎不可能出现。 6.1 统计量 的一个样本, 定义：设Xi, X2J M , Xn是从总体X中抽取的容量为n 如果由此样本构造 个不依赖于

13、任何未知参 数的函数 T(Xi，X2，||| ,Xn）,则称函数T（Xi，X2，|『Xn）是 个统计量。 特点： 由样本构造而得，是样本的函数 不含任何未知的参数 当获得样本的一组具体观测值 (Xl,X2，M，Xn) ,带入T，计算出 T(Xl,X2, I ,Xn) 的数值，称为统计量的值 2 常用的统计量X,S 6.2 抽样分布 抽样分布：统计量的分布 随机变量X Xi，X2，| ,Xn X X11, X12，| (|，X1n X X21 , X22 JU, X2n X2 ・ • ・ • • * Xm1, Xm2，|||，Xm

14、n Xm 精确分布：可以得到分布的数学表达式 渐近分布：难以得到精确分布时，借助于极限工具，求得抽样分布的近似分布, 称为渐近分布。 定理1: 设X1,X2,“|,Xn是取自总体X的一个样本，记E（XJ D(X。 ① E(X) 2 ，D(X)一 ② E(s2) 2 2\ ,E(sn) 时, 时, 2 sn 设 X1,X2,|||,Xn 是取自正态总体N（ 2 ）的一个样本 _ 2 X ①x n n （， ~n~）或等价地/品 N N(0,1) (n 1)s2 ns2 2 (Xi X)2 N 2(n 1) ③当n lim

15、P(|X n । ④当n 定理2: ③X与s2相互独立 推论1: 设 X1,X2,|||,Xn 是取自正态总体N（ 2）.… ）的一个样本，那么 "nW D 简要证明： xNn（ , 2）之加（0,1） 2 》 1） X ,二In M 1) (n ?s /(n 1) 独立（t分布的定义） 推论2 设X1，X2，"l,Xm是取自正态总体N（〜C的一个样本, Y，Y2」||,Yn是取自正态总体N（ 2，2）的一个样本, (X Y422") 12 \ m n 简要证明： _2 X\N( 1, 1

16、2)XNN(1,常 _2 y\n( 2, 2) yNn( 2,力 __22 X Y|N( 12.——) m n (X 丫9；2)NN(0,1) 112 \ m n 推论3: 设X1，X2，|||,Xm是取自正态总体 N( 1, 2）的-个样本, 丫1,丫2,|||,工 是取自正态总体N（ 2 2）的一个样本, (X Y) (i 1 1 n 2) Mm n ,、2,、 2 2 (m 1)s (n I)/ sp 其中，(m n 2) 简要证明： _2 X\N( 1, 可加性 2 )X(^N( 1,-) 2 Y“N( 2, 2) YNn

17、( 2,-) __22 知,X Y^(12，- T) 5任 2(m 1) 邛N 2(n 1) 1)s2 2 2(m n 2) ,2 (m 1)[(n (X Y) ( 1 2) Nt(m 2) 整理得 n 2) (X Y) ( 12) Nt(m ；(m 1)s2 (n 1)s2 11 m m n 2\ m n sp (m 1)s2 (n 1)s2 设(m n 2) 推论4: n 2) 设 X1,X2,|||,Xm 是取自正态总体 Y，Y2，|||，Yn 是取自正态总体N( 2、 N( 1, 1 )的一个样本, 2 2,

18、2)的一个样本， gm 1,n 1) 2 /2 Si / 1 2 /2 s2 / 2 简要证明： 正态 XWN( 12) 2 (m 1后 2/ -——N (m 1) 1 yNn( (n 1)S2 2(n 1) (n 1)s2 /(n 1) 一 1F(m 1,n 1) 1) s2/ 2 /2 即 S2/2 F(m 1,n 1) 非正态总体的情形 定理：设 X1,X2,|U,Xn是取自总体X的一个样本，当n较大 时，近似地有 X °/Un \N(0,1) X s/ 7n \N(0,1) 2 (2) X 分布的形状取决于其自由度 n的大小，通常为不对称的右偏分布， 随着自由度的增大逐渐趋于对称。 (3)X2分布的期望为E( 2) n,方差为D( 2) 2n⑺为自由